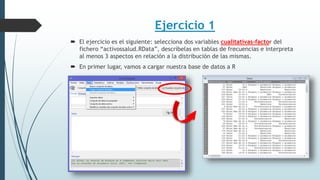
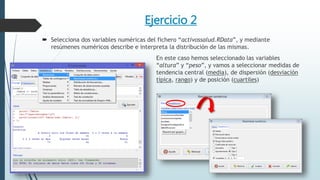
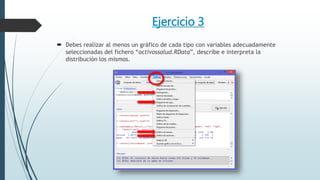
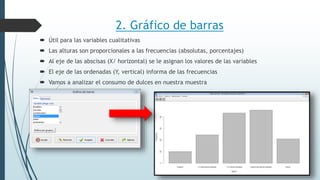
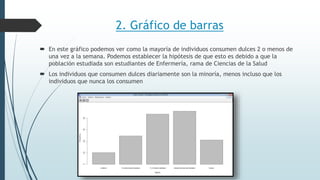
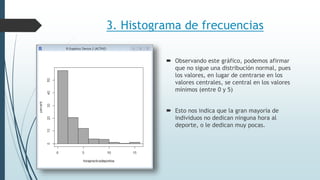
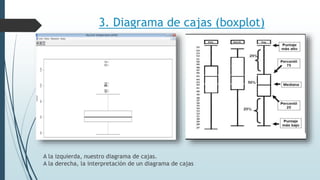
Este documento resume tres ejercicios de análisis exploratorio de datos utilizando el paquete R. En el primer ejercicio, se describen dos variables cualitativas en tablas de frecuencias. En el segundo, se analizan dos variables numéricas usando resúmenes estadísticos. En el tercer ejercicio, se crean gráficos como diagramas de sectores, barras, histogramas y cajas para interpretar la distribución de variables.

1. ANÁLISIS EXPLORATORIO DE
DATOS.
TABLAS DE FRECUENCIAS,
RESÚMENES NUMÉRICOS Y
GRÁFICOS
Mariló Páyer Pérez
Macarena A
Subgrupo 3

2. Ejercicio 1
 El ejercicio es el siguiente: selecciona dos variables cualitativas-factor del
fichero “activossalud.RData”, descríbelas en tablas de frecuencias e interpreta
al menos 3 aspectos en relación a la distribución de las mismas.
 En primer lugar, vamos a cargar nuestra base de datos a R

3.  Nos piden que describamos dos variables en una tabla de frecuencias.
 En este caso, hemos seleccionado las variables “botellón” y “cerveza”

4. Analizando estos datos, observamos que:
 El porcentaje de los bebedores diarios de botellón es muy semejante al de los
bebedores diarios de cerveza (1'05% frente a 1'38%), lo que nos lleva a pensar que
los individuos de la muestra propensos a beber diariamente no distinguen entre
cerveza o bebidas destiladas.
 Por el contrario, el porcentaje de individuos que nunca ha bebido cerveza es más
del doble (37'02%) que el de quienes nunca han probado botellón (17'82%), por lo
que podemos establecer la hipótesis de que es más frecuente salir de botellón que
beber cerveza en fiestas, donde suelen beber los jóvenes.
 Ya puestos, podemos comprobar cómo el porcentaje de individuos que beben
botellón sólo los fines de semana (31'58%) es superior a los que beben cerveza los
fines de semana (20'76%), lo que corrobora nuestra hipótesis anterior.

5. Ejercicio 2
 Selecciona dos variables numéricas del fichero “activossalud.RData”, y mediante
resúmenes numéricos describe e interpreta la distribución de las mismas.
En este caso hemos seleccionado las variables
“altura” y “peso”, y vamos a seleccionar medidas de
tendencia central (media), de dispersión (desviación
típica, rango) y de posición (cuartiles)

6. Este es el resultado:
• Así, los datos nos indican que la media de la muestra es de 1’67 m de altura y de unos
62’76 kg de peso
• La desviación típica de la altura es muy baja (0’08), mientras que la del peso es más alta
(12’66), lo que nos indican que los primeros valores no están muy dispersos (muestra
homogénea), mientras sí lo están los del peso (muestra heterogénea)
• La muestra estudiada en la altura ha sido de 290 individuos, mientras que la del peso ha
sido de 275
• 1 individuo no ha respondido con respecto a su altura, mientras que los que no lo han
hecho con respecto al peso son 16

7. Este es el resultado:
• En cuanto a los cuartiles, nos da información sobre los máximos y los mínimos. El
mínimo de altura se sitúa en 1’46m, siendo el máximo de 2m. En cuando al peso, el
mínimo se sitúa en 38 kg y el máximo en 130 kg.
• Esto nos lleva a corroborar que la muestra es más homogénea con respecto a la altura
que con respecto al peso.

8. Ejercicio 3
 Debes realizar al menos un gráfico de cada tipo con variables adecuadamente
seleccionadas del fichero “activossalud.RData”, describe e interpreta la
distribución los mismos.

9. 1. Gráfico de sectores
 Este tipo de gráficos de sectores no son útiles cuando la variable tiene múltiples categorías,
por lo que vamos a utilizar una variable dicotómica: el sexo
Así, podemos ver claramente como el
número de mujeres de la muestra es muy
superior al de varones

10. 2. Gráfico de barras
 Útil para las variables cualitativas
 Las alturas son proporcionales a las frecuencias (absolutas, porcentajes)
 Al eje de las abscisas (X/ horizontal) se le asignan los valores de las variables
 El eje de las ordenadas (Y, vertical) informa de las frecuencias
 Vamos a analizar el consumo de dulces en nuestra muestra

11. 2. Gráfico de barras
 En este gráfico podemos ver como la mayoría de individuos consumen dulces 2 o menos de
una vez a la semana. Podemos establecer la hipótesis de que esto es debido a que la
población estudiada son estudiantes de Enfermería, rama de Ciencias de la Salud
 Los individuos que consumen dulces diariamente son la minoría, menos incluso que los
individuos que nunca los consumen

12. 3. Histograma de frecuencias
 Consisten en rectángulos unidos cuya área es proporcional a la frecuencia
absoluta del intervalo correspondiente
 Se utiliza para variables cuantitativas, como las horas que le dedican al deporte
los individuos de nuestra muestra
 Para visualizarlos mejor, vamos a seleccionar la opción de mostrarlos por
porcentajes

13. 3. Histograma de frecuencias
 Observando este gráfico, podemos afirmar
que no sigue una distribución normal, pues
los valores, en lugar de centrarse en los
valores centrales, se central en los valores
mínimos (entre 0 y 5)
 Esto nos indica que la gran mayoría de
individuos no dedican ninguna hora al
deporte, o le dedican muy pocas.

14. 3. Diagrama de cajas
 Expresan valores atípicos
 Los casos atípicos (outliers) son observaciones con valores extremos
 Notablemente diferentes de las restantes observaciones
 A veces, pueden convertirse en observaciones influyentes que distorsionan los
resultados (relaciones entre variables, normalidad, etc.)
 En variables cuantitativas, como el peso

15. 3. Diagrama de cajas (boxplot)
A la izquierda, nuestro diagrama de cajas.
A la derecha, la interpretación de un diagrama de cajas

16. 3. Diagrama de cajas (boxplot)
 El 25% de individuos tienen un peso de
(aproximadamente) 55 kg o menos
 El 50% de la población (mediana)
tienen un peso de unos 60 kg o menos
 El 75% de los alumnos tienen un peso
de 70 kg (aproximadamente) o menos
 Por último, casi el 100% de los
individuos pesan 90 kg o menos. Sin
embargo, encontramos diversos
valores atípicos que superan los 100
kg, llegando a alcanzar más de 120 kg.
 Así mismo, los valores están muy
concentrados entre 55 y 65 kg.