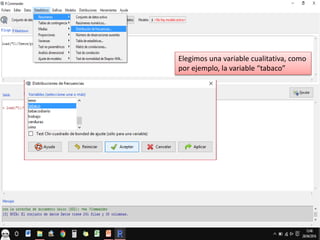
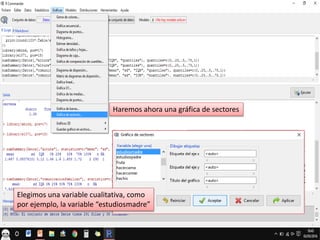
El documento describe el análisis exploratorio de variables cualitativas y cuantitativas del archivo de datos "activossalud.RData". Se seleccionan variables como "tabaco", "cerveza", "altura", "comunicacionfamiliar", "estudiosmadre", "embutidos", "horapracticadeportiva", y "malestaresactivos" y se analizan sus distribuciones mediante tablas de frecuencias, resúmenes numéricos, gráficos de sectores, barras, histogramas y diagramas de caja.

2. Para empezar, seleccionaremos dos variables
cualitativas-factor de “activossalud.RData”, y las
describiremos en tablas de frecuencias e
interpretaremos al menos 3 aspectos en relación
a la distribución de las mismas.

3. Cargamos el archivo en R-Commander

4. Elegimos una variable cualitativa, como
por ejemplo, la variable “tabaco”

6. En la tabla de frecuencias de la variable “tabaco”
vemos que casi la mitad de los participantes no
han consumido nunca tabaco.
Solo el 5,88% de los participantes consumen
tabaco 2 o 3 veces al mes. Es el dato de la
variable que menos valores tiene.
Lo más frecuente en los que consumen tabaco
es hacerlo alguna vez (19,03%), aunque no está
muy lejos de los que fuman a diario (17,30%)

7. Elegimos una variable cualitativa, como
por ejemplo, la variable “cerveza”

9. En la tabla de frecuencias de la variable
“cervezas” vemos que lo más frecuente es que
los participantes no beban nunca cerveza.
Solo el 1,38% de los individuos bebe cerveza
diariamente.
También prima el beber cerveza los fines de
semana, después de los que nunca la beben
(20,76%)

10. A continuación seleccionaremos dos variables
numéricas del fichero “activossalud.RData”, y
mediante resúmenes numéricos describe e
interpreta la distribución de las mismas.

11. Elegimos una variable cuantitativa,
como por ejemplo, la variable “altura”
Y elegimos que nos aparezca la
media, la desviación típica y el
rango intercuartílico.

13. En la variable “altura” vemos que la media (mean =
1,667) y Q2 (50% = 1,655) son prácticamente
iguales, lo que nos indica que la distribución es
simétrica.
Otro rasgo de simetría que vemos en el resumen de
numérico es que entre el Q1 – Q2 y Q2 – Q3 existe,
más o menos, el mismo rango.
La desviación típica es 0,08 y la media 1,667, lo que
significa que entre 1,58 – 1,75, se encuentran el
68,3% de los individuos.
También vemos que no han participado todos los
individuos, sino que uno de ellos no ha contestado
a esta pregunta.

14. Y elegimos que nos aparezca la
media, la desviación típica y el
rango intercuartílico.
Elegimos una variable cuantitativa,
como por ejemplo, la variable
“comunicacionfamiliar”

16. En la variable “comunicacionfamiliar” vemos que la
mitad de los individuos no ha respondido a esta
pregunta.
La media es 7,83 y la desviación típica es 2,82, lo
que significa que entre 5,01 – 10,65 se encuentran
el 68,3% de los individuos.
La media y el primer cuartil difieren en 0,83
puntuaciones y entre Q1 – Q2 y Q2 – Q3 hay 1 y 2
valores, respectivamente. Por tanto, podemos decir
que es una distribución simétrica.

17. Por último, debemos realizar al menos un
gráfico de cada tipo con variables
adecuadamente seleccionadas del fichero
“activossalud.RData”, describe e interpreta la
distribución los mismos.

18. Elegimos una variable cualitativa, como
por ejemplo, la variable “estudiosmadre”
Haremos ahora una gráfica de sectores

20. En la distribución de la variable “estudiosmadre”
vemos que casi la mitad de las madres de los
individuos no tienen estudios o tienen estudios
primarios.
Lo que menos abunda es que las madres tengan
estudios universitarios, aunque casi es un cuarto
de los individuos.

21. Haremos ahora una gráfica de barras
Elegimos una variable cualitativa, como
por ejemplo, la variable “embutidos”

23. En la distribución de la variable “embutidos”
vemos que lo que más se repite es la
consumición de embutidos 1 o 2 veces por
semanas, muy cerca de la consumición de 3 o
más a la semana.
Lo que menos frecuencia tiene es que no se
tomen embutidos nunca.

24. Ahora, haremos un histograma de
frecuencias
Elegimos una variable cuantitativa, como
por ejemplo, la variable
“horapracticadeportiva”

26. En la representación de la variable
“horapracticadeportiva”, vemos que lo más
frecuente es que se hagan menos de cinco horas
de deporte. Así, vemos también que lo menos
frecuente es que se hagan 10 – 15 horas de
deporte.
Vemos una gráfica muy asimétrica.

27. Ahora, haremos un diagrama de caja
Elegimos una variable cuantitativa, como por
ejemplo, la variable “malestaresactivos”

29. En esta representación del la variable
“malestaresactivos” vemos que existen cuatro
valores atípicos, es decir, observaciones con valores
extremos.
La media se encuentra entre los valores 40 – 45.
Podemos observar, además, que la distancia entre
Q1 – Q2 y Q2 – Q3 es muy similar, por lo que
podemos decir que la distribución es simétrica.
Además también podemos ver que puntaje más
alto y el puntaje más bajo se encuentran a la misma
distancia de la media, aproximadamente.