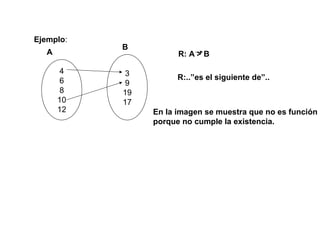
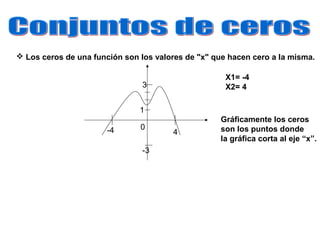
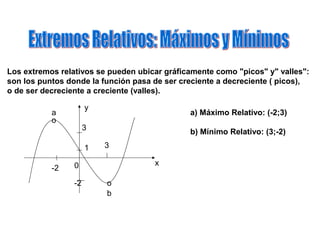
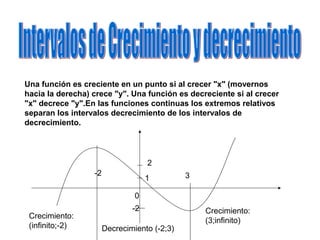
El documento define una relación entre dos conjuntos numéricos A y B como un conjunto de pares ordenados (x, y) donde x pertenece a A y y pertenece a B. Una relación es una función si cada elemento de A está relacionado con exactamente un elemento de B (existencia y unicidad). Se proveen ejemplos de relaciones que cumplen y no cumplen con estas propiedades de función. Además, se define dominio como el conjunto de valores posibles de x e imagen como el conjunto de valores posibles de y para una función f: A → B.

1. Una relación entre dos conjuntos numéricos A y B es un conjunto de pares
ordenados (x;y ), con la condición de que x E A ^ y E B.
Una relación es una función cuando se cumplen 2 condiciones:
 Todos los elementos del conjunto A están relacionados con algún elemento
del conjunto B (existencia).
 Cada elemento del conjunto A se relaciona con un único elemento del
conjunto B (unicidad).

2. Ejemplo:
4
6
8
10
12
3
9
19
17
A
B
R: A > B
En la imagen se muestra que no es función
porque no cumple la existencia.
R:..”es el siguiente de”..

3. En una función f: R > R, su Dominio es un conjunto de
números reales que pueden ser valores de X y su
Codominio o imagen, los que pueden ser valores de Y.
-4
-2
3
6
x
y
f
En la función f del gráfico , el dominio son
f: { -4;6 } y el codominio f: {-2;3} .

4. • Diagrama de Venn
• Pares Ordenados.
• Tabla
• Dominio y Codominio
• Indicar si es o no función.
1)
X
x
B
1
2
A
2) R: { x,2 }
3)
X
x
x
B
Y
2
A4) DM (dominio) = {x,B }
CDM (codominio)= {2,A }
5) No es función porque no se cumple la existencia.

5.  Los ceros de una función son los valores de "x" que hacen cero a la misma.
0-4 4
-3
1
3
X1= -4
X2= 4
Gráficamente los ceros
son los puntos donde
la gráfica corta al eje “x”.

6. Se llama conjunto de positividad al conjunto de todos los valores de “x” para los
cuales la función es positiva.
Analógicamente el conjunto de negatividad es el conjunto de todos los valores
de “x” para los cuales la función es negativa.
0
3
-4 4
-2
1
Conjunto de positividad : (-4;4)
Conjunto de
negatividad:
(-infini.;-4)u
(4;infini) Positividad: Gráficamente corresponde al
intervalo (o los intervalos) de valores de
“x” en los cuales la “curva” esta por
encima del eje “x”.
Negatividad: Lo mismo pero cuando la
“curva” esta por debajo del eje “x”.

7. Los extremos relativos se pueden ubicar gráficamente como "picos" y" valles":
son los puntos donde la función pasa de ser creciente a decreciente ( picos),
o de ser decreciente a creciente (valles).
0
-2
-2
31
3
x
y
o
o
a
b
a) Máximo Relativo: (-2;3)
b) Mínimo Relativo: (3;-2)

8. Una función es creciente en un punto si al crecer "x" (movernos
hacia la derecha) crece "y". Una función es decreciente si al crecer
"x" decrece "y".En las funciones continuas los extremos relativos
separan los intervalos decrecimiento de los intervalos de
decrecimiento.
-2
-2
1
2
0
3
Decrecimiento (-2;3)
Crecimiento:
(infinito;-2)
Crecimiento:
(3;infinito)

9. Micaela Campazzo
Paula Vazquez
Daiana Gonzalez

10. Micaela Campazzo
Paula Vazquez
Daiana Gonzalez