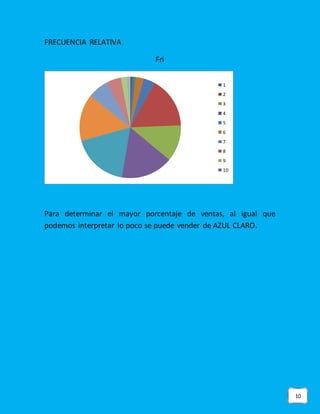
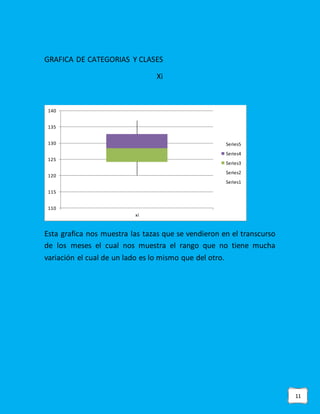
Este documento presenta los datos de ventas de tazas de café en una tienda de conveniencia durante 10 periodos de 30 días cada uno. Se realizaron análisis estadísticos como media, moda, mediana, desviación estándar y varianzas. También se incluyeron gráficas como barras, polígono y cajas. Las conclusiones fueron que las ventas tuvieron pocas variaciones y se vendieron principalmente 129-130 tazas, por lo que abrir un negocio de venta de café sería viable dado el nivel constante de demanda

1. ARTURONAJERAMARTINEZ
2015
DATOSNOAGRUPADOS
GERARDO EDGAR MATA ORTIZ
ESTADISTICAS
PROCESOS DE PRODUCCION
AREA MANUFACTURA
2° E

2. 1
INDICE
INTRODUCCION……………………………………………………………………………. 2
DATOS NO AGRUPADOS……………………………………………………………… 3, 4
RESPUESTAS 1, 2, 3,4……………………………………………………………………. 5
RESPUESTAS TABLA DE FRECUENCIAS…………………………………………. 6
DESVIACION MEDIA, VARIANZA Y ESTANDAR……………………………... 7
GRAFICA Fi DE FRECUENCIA ABSOLUTA.………………………………………. 8
GRAFICA DE DESVIACION ESTANDAR…………………………………………….. 9
GRAFICA Fa FRECUENCIA RELATIVA...…………………………………………….. 10
GRAFICA Xi CATEGORIAS...……………………………………………………………. 11
RESPUESTAS DE CONCLUSIONES 9,10………………………………………….. 12

3. 2
INTRODUCCION
La matemática es la ciencia del orden y la medida, de
bellas cadenas de razonamientos, todos sencillos y
fáciles.
René Descartes
La estadística consiste en recolectar, organizar, resumir y analizar datos, a
partir de los cuales se deducen conclusiones que validen decisiones
razonables.
Además trataremos sobre los diferentes aspectos de esta materia, como lo
es la población, la muestraque de esta se toma, para determinado estudio.
Así como las técnicas utilizadas para la recolección, distribución y análisis
de datos. Estos datos puedenser verbales, numéricos, simples y agrupados
en sus respectivas tablas de distribución de clases y frecuencias y la
representación gráfica de las mismas.
También están las medidas que resumen los datos recolectados: las
medidas de tendencia central, que permiten la comparación de datos
cuantitativos, promediándolos.

4. 3
DATOS NO AGRUPADOS
El director general de la empresa CAFÉ GENESIS desea determinar si
es conveniente instalar un negocio especializado en venta de café y
sus complementos (galletas, pastel etc...) en cierta ubicación. La
tabla adjunta muestra el número de tazas de café vendidas en una
tienda de conveniencia durante 10 periodos de 30 días cada uno.
Los datos están ordenados conforme se obtuvieron; la primera fila
es el primer periodo de 30 días, la segunda fila, el segundo periodo
y así sucesivamente.
1.- ¿Cuál es la población?
2.- ¿Se estudió la población completa? ¿O se trata solo de una
muestra?
3.- ¿Cuál es la variable de interés?
4.- ¿Determina el tipo de variable y su escala de medición?
5.- ¿Elabora la tabla de distribución de frecuencia e interpreta los
resultados?
6.- ¿Determina la media aritmética, mediana y moda y explica su
significado?
7.- ¿calcule la desviación media, varianza y desviación estándar, e
interprétalas?
8.- ¿Traza e interpreta las gráficas siguientes:
8.1 Una gráfica de barras con la frecuencia absoluta.

5. 4
8.2 Una gráfica circular con la frecuencia relativa.
8.3 Una gráfica de polígono con la frecuencia relativa acumulada.
8.4 Una gráfica radial con los datos que consideres apropiados.
8.5 una gráfica de cajas y bigotes.
9.- ¿Elabora y explica tus conclusiones acerca de la demanda del
articulo con base a la información disponible?
10.- ¿Compara tus conclusiones con las de tus compañeros de
equipo suponiendo que se trata de las ventas del mismo artículo en
dos tiendas de conveniencia ubicadas en vecindarios del mismo
nivel socioeconómico en la misma ciudad?

6. 5
RESPUESTAS
1.- R= Todas las tazas de café.
2.- R= Solo de una muestra.
3.- R= El número de tazas que se venderán por día.
4.- R= Es una variable cuantitativa.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
130 129 131 130 124 124 129 128 132 128 131 127 127 128 131 130 133 127 131 131 129 132 128 130 126 129 129 126 130 127
132 132 129 133 131 127 125 133 127 130 128 128 130 130 131 129 134 132 127 126 127 128 128 131 127 132 129 132 129 128
131 129 128 133 129 127 131 125 130 132 129 126 129 120 129 131 130 130 126 129 131 133 128 127 131 127 131 130 129 129
128 130 130 130 131 127 133 129 129 128 131 125 127 126 127 126 125 128 131 129 131 136 127 132 131 128 129 131 129 129
127 128 127 130 133 127 129 130 127 132 128 127 133 134 129 127 133 127 131 130 127 130 130 129 131 129 127 128 136 129
130 130 130 127 129 127 127 127 129 133 130 129 126 127 127 134 137 127 130 128 130 131 123 130 130 131 130 131 128 134
126 130 128 129 129 127 130 127 127 130 131 130 130 128 125 131 130 128 130 126 129 131 131 131 130 131 125 131 134 132
127 131 131 127 131 127 132 130 128 127 129 129 131 130 132 129 129 130 133 128 129 128 133 132 131 127 130 127 128 128
127 129 130 130 131 130 129 130 128 131 131 132 131 130 130 134 125 130 129 127 127 130 128 129 128 127 133 124 130 129
129 133 131 127 128 132 125 130 132 132 130 129 132 131 129 131 128 128 129 131 127 127 132 129 128 129 127 126 130 130

7. 6
5.- R=
xi fi fai fri frai fixi
120 1 1 0.00333333 0.00333333 120 9.28 86.1184
121 0 1 0 0.00333333 0 0 0
122 0 1 0 0.00333333 0 0 0
123 1 2 0.00333333 0.00666667 123 6.28 39.4384
124 3 5 0.01 0.01666667 372 15.84 83.6352
125 8 13 0.02666667 0.04333333 1000 34.24 146.5472
126 11 24 0.03666667 0.08 1386 36.08 118.3424
127 49 73 0.16333333 0.24333333 6223 111.72 254.7216
128 35 108 0.11666667 0.36 4480 44.8 57.344
129 50 158 0.16666667 0.52666667 6450 14 3.92
130 54 212 0.18 0.70666667 7020 38.88 27.9936
131 45 257 0.15 0.85666667 5895 77.4 133.128
132 20 277 0.06666667 0.92333333 2640 54.4 147.968
133 14 291 0.04666667 0.97 1862 52.08 193.7376
134 6 297 0.02 0.99 804 28.32 133.6704
135 0 297 0 0.99 0 0 0
136 2 299 0.00666667 0.99666667 272 13.44 90.3168
137 1 300 0.00333333 1 137 7.72 59.5984
300 129.28
desviación
media 1.81493333
varianza 5.272508361
desviación
estándar 2.296194321
𝑥̅=
(𝑥 𝑖 − 𝑥̅)^2 𝑓𝑖
[ 𝑥 𝑖 − 𝑥̅] 𝑓𝑖

8. 7
6.-
R= La mediana: representa una medida de la tendencia central
de los datos, el cual es el número de en medio.
Y la mediana es 129
R= La moda: es el valor que tiene mayor frecuencia absoluta.
Y la moda 130
R= La media aritmética: es el valor obtenido al sumar todos los
datos y dividir el resultado entre el número total de
datos.
Y la mediana aritmética es= 129.28
7.-
R=La desviación media es = 1.81493333
R=la varianza es = 5.272508361
R=La desviación estándar es =2.296194321
Varia mui poco la desviación es un poco

9. 8
8.- GRAFICAS
GRAFICA DE FRECUENCIA ABSOLUTA
Fi
Generalmente se venden 129 y 130
0
10
20
30
40
50
60
120121122123124125126127128129130131132133134135136137
fi
fi

10. 9
GRAFICA DE DESVIACION ESTANDAR
GRAFICA DE FRECUENCIA RELATIVA ACOMULADA
Frai
0
50
100
150
200
250
300
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Series1
0
0.2
0.4
0.6
0.8
1
1.2
1 2 3 4 5 6 7 8 9 101112131415161718
Series1
(𝑥 𝑖 − 𝑥̅)^2 𝑓𝑖
Nos muestra la
gráficala frecuencia
relativa que al dividir
el número de la
frecuencia
acumulada entre los
300 datos que se
vendieron.

11. 10
FRECUENCIA RELATIVA
Fri
Para determinar el mayor porcentaje de ventas, al igual que
podemos interpretar lo poco se puede vender de AZUL CLARO.
1
2
3
4
5
6
7
8
9
10

12. 11
GRAFICA DE CATEGORIAS Y CLASES
Xi
Esta grafica nos muestra las tazas que se vendieron en el transcurso
de los meses el cual nos muestra el rango que no tiene mucha
variación el cual de un lado es lo mismo que del otro.
110
115
120
125
130
135
140
xi
Series5
Series4
Series3
Series2
Series1

13. 12
9.-
En primeria instancia la estadística es muy importante para este
problema ya que con ello obtendrán cifras que les ayudara a ver si
es factible la instalación de dicho negocio, en base a estos datos
obtenidos se ve pre sus ventas tendrán variaciones las cuales le
muestran ventas fuertes por lo tanto es factible que se instale el
negocio de venta de café.
10._
En esta parte al comparar las ventas de tazas de café con mi
compañero los resultados de él y míos los datos son similares tienes
sus ventas altas y bajas ya que tiene temporadas de ventas altas
pero para los dos es viable abrir el negocio de venta de tazas de
café.