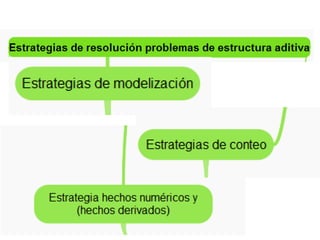
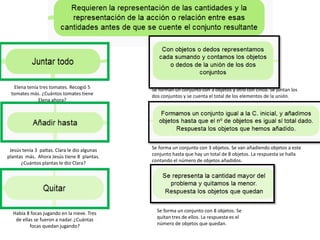
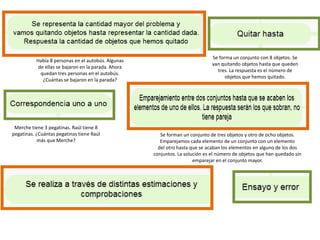
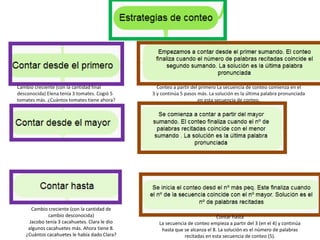
Este documento presenta diferentes estrategias para resolver problemas aditivos en matemáticas desde un enfoque cognitivo. Describe el uso de estrategias como la modelización, el conteo verbal o mental, y la aplicación de hechos numéricos básicos. También presenta la secuencia general de resolución de problemas según el método de Polya.

1. ESTRATEGIAS EN LA RESOLUCIÓN DE PROBLEMAS
ADITIVOS
LA ENSEÑANZA DE LAS MATEMÁTICAS DESDE UN ENFOQUE COGNITIVO
Froy Castro Ventura

3. Elena tenía tres tomates. Recogió 5
tomates más. ¿Cuántos tomates tiene
Elena ahora?
Se forman un conjunto con 3 objetos y otro con cinco. Se juntan los
dos conjuntos y se cuenta el total de los elementos de la unión.
Jesús tenía 3 paltas. Clara le dio algunas
plantas más. Ahora Jesús tiene 8 plantas.
¿Cuántos plantas le dio Clara?
Se forma un conjunto con 3 objetos. Se van añadiendo objetos a este
conjunto hasta que hay un total de 8 objetos. La respuesta se halla
contando el número de objetos añadidos.
Había 8 focas jugando en la nieve. Tres
de ellas se fueron a nadar. ¿Cuántas
focas quedan jugando?
Se forma un conjunto con 8 objetos. Se
quitan tres de ellos. La respuesta es el
número de objetos que quedan.

4. Había 8 personas en el autobús. Algunas
de ellas se bajaron en la parada. Ahora
quedan tres personas en el autobús.
¿Cuántas se bajaron en la parada?
Se forma un conjunto con 8 objetos. Se
van quitando objetos hasta que queden
tres. La respuesta es el número de
objetos que hemos quitado.
Merche tiene 3 pegatinas. Raúl tiene 8
pegatinas. ¿Cuántas pegatinas tiene Raúl
más que Merche?
Se forman un conjunto de tres objetos y otro de ocho objetos.
Emparejamos cada elemento de un conjunto con un elemento
del otro hasta que se acaban los elementos en alguno de los dos
conjuntos. La solución es el número de objetos que han quedado sin
emparejar en el conjunto mayor.

5. Utilización de la estrategia de
"añadir hasta" para resolver un problema de
cambio creciente (con la cantidad de cambio
desconocida).

6. Utilización de una estrategia de
correspondencia uno a uno para
resolver un problema de comparación
(con la diferencia desconocida)

7. Cambio creciente (con la cantidad final
desconocida) Elena tenía 3 tomates. Cogió 5
tomates más. ¿Cuántos tomates tiene ahora?
Conteo a partir del primero La secuencia de conteo comienza en el
3 y continúa 5 pasos más. La solución es la última palabra pronunciada
en esta secuencia de conteo.
Cambio creciente (con la cantidad de
cambio desconocida)
Jacobo tenía 3 cacahuetes. Clara le dio
algunos cacahuetes más. Ahora tiene 8.
¿Cuántos cacahuetes le había dado Clara?
Contar hasta
La secuencia de conteo empieza a partir del 3 (en el 4) y continúa
hasta que se alcanza el 8. La solución es el número de palabras
recitadas en esta secuencia de conteo (5).

8. Cambio decreciente (con la cantidad
final desconocida)
Había 8 pingüinos jugando. Tres de
ellos se alejaron nadando. ¿Cuántos
pingüinos quedan jugando?
Conteo regresivo (o contar hacia atrás)
La secuencia de conteo regresivo
comienza a partir del 8 (en el 7) y se
dan 3 pasos. La solución es la última
palabra pronunciada en esta secuencia
de conteo.
Cambio decreciente (con la cantidad de
cambio desconocida)
Había 8 personas en el autobús.
Algunas de ellas se bajaron. Quedan 3
personas en el autobús. ¿Cuántas se
bajaron?
Conteo regresivo hasta (o contar hacia
atrás hasta) La secuencia de conteo regresivo
comienza a partir del 8 (en el 7) y
continúa hasta que se alcanza el 3. La
solución es el número de palabras
recitadas en esta secuencia de conteo (5).

9. HECHOS NUMÉRICOS
Los procedimientos utilizados para resolver los
problemas verbales no se limitan a las estrategias
de modelización y de conteo. A medida que los
niños van aprendiendo hechos numéricos en la
escuela y fuera de ella, van aplicando este
conocimiento a la resolución de problemas.

10. Dobles: Otros de los primeros hechos aditivos que los niños
pueden memorizar son los dobles: 2+2, 5+5, etc. En el caso de
las restas, ellos implica la facilidad de resolver: 4-2; 10-5, etc.
Dobles más/ menos uno: A partir de los dobles se pueden
deducir una serie de resultados aditivos y sustractivos cuando un
elemento de la operación sea el doble más/ menos uno del otro
elemento. Ejemplo:
3+2, es lo mismo que (2+2) + 1 o también (3+3) – 1
9-5, es lo mismo que (10-5)-1
Dobles más o menos dos: Ejemplos:
8+6, es lo mismo que (6+6) + 2
Para el caso de las restas no es muy aplicativo.
Los nueves: Sumar nueve es como sumar diez menos uno.
La familia del diez: Aproximarse a las sumas básicas por familias
es un enfoque digno de tener en cuenta. Se trata de organizar los
datos por parejas que sumen lo mismo.

11. ¿Cuál es la secuencia?
Modelado de las
acciones con
materiales
Modelado de las acciones
con ayudas externas
(dedos, marcas, etc.)
Estrategias de conteo
verbal o mental
Memorización de hechos
básicos
Uso de sentencias
numéricas
Generalización de estrategias para todos las estructuras

12. COMO PROCESO COMO PRODUCTO
Lenguaje
CEP DE CASTILLEJA DE LA
CUESTA
12
DESARROLLO DE
CAPACIDADES
METODOLOGÍA
POLYA
ESTRATEGIAS DE
RESOLUCIÓN
Intuición
Descubrimiento
EL ERROR ES PARTE
DEL PROCESO
ELABORAR UN PLAN
ENUNCIACIÓN
VERIFICAR TRANSFERENCIA O
ABSTRACCIÓN
COMPRENSIÓN
EJECUTAR EL PLAN
ELABORACIÓN
CONCRETIZACIÓN
ATENDER A LA
DIVERSIDAD
MOTIVADORA
Atención-
Observación
Razonamiento
Memoria
Creatividad
LA RESOLUCIÓN DE PROBLEMAS

13. ESTRATEGIAS PARA
COMPRENDER, RESOLVER Y
FORMULAR PROBLEMAS EN
PRIMARIA

14. Transformaciones en problemas sin resolver.
"Mi hermano tiene 12 años y yo tengo 8. ¿Cuántos
años más tiene mi hermano?"
se convierte en "Mi hermano tiene 12 años y yo
tengo 8. ¿Cuántos años menos tengo yo?"

15. Crear un problema nuevo a partir de otro ya
resuelto
Va a comenzar las clases y le compran a un alumno
los zapatos, que cuestan 24 soles , y las zapatillas
de deporte, que cuestan 19 soles . ¿Cuánto cuestan
los dos pares?
El problema no es difícil de resolver: 43 soles .
Añadimos una nueva situación
Pagan la cuenta con 50 soles . ¿Cuánto les
devuelven?

16. DI LO MISMO PERO DE OTRA FORMA
-Miren es más alta que Mikel.
Mikel es ...
- Javier tiene 30 soles más que Andrés.
Andrés tiene ...
- El globo está encima de Begoña.
Begoña está ...
- Ayer tenía más canicas que hoy.
Hoy tengo ...
- Tengo 8 bolitas más que tú.
Tu tienes ...
16

17. DAR LOS DATOS ESCRIBIR UNA PREGUNTA
•El hermano de Javier pesa 45 kg. Javier pesa 29 kg.
•Rosita tiene 258 soles. Javier tiene 35 soles menos que
Begoña.
•Mi padre tiene 38 años. Mi hermano pequeño ha
cumplido 5 años.
•- Un señor tiene 30 días de vacaciones. Los 12 primeros
días los ha pasado descansando en casa, pero el resto de
las vacaciones ha estado viajando.
•- Un pastor tiene 75 ovejas 17
blancas y 17 ovejas negras.

18. DAR LA PREGUNTA ESCRIBIR LOS DATOS
Determinar primero el contexto
•¿Cuántos caramelos he llevado esta mañana al
colegio?
•¿Cuántos céntimos me devolverán en la tienda?
•¿Cuánto tendré que pagar por los dos bolis y por el
cuaderno?
18

19. SOBRAN DATOS TACHARLOS
•En una clase hay 25 alumnos. Todos tienen 10
años. El profesor les ha dado tres caramelos a cada
uno. ¿Cuántos caramelos ha repartido el profesor?
•El colegio de Javier está a 8 km de su casa. Javier
coge el autobús todos los días a las 8 de la mañana.
En el autobús viajan 65 alumnos. El autobús tarda
una hora en llegar al colegio. ¿A qué hora llega
Javier al colegio?
• María tiene 13 años y pesa 40 kg. El hermano de
María mide 2 metros y es 6 años mayor que María.
¿Qué edad tiene el hermano de María?
19

20. FALTA UN DATO ESCRIBIRLO
•El cuaderno de tuamiga costó 3 soles más que el
cuaderno de Javier. ¿Cuánto costaba el cuaderno de tu
amiga?
•El señor de la tienda le devolvió a Javier 40 céntimos
.¿Cuánto costaba el kilo de papas que compró Javier?
•El auto salió a las 8 de la mañana. ¿Cuántas horas duró el
viaje?
•He metido 8 soles en la alcancía de mi hermana. ¿Cuánto
dinero tenía mi hermana en su alcancía?
20
APLICACIÓN

21. DADAS DOS VIÑETAS HACER UNA PREGUNTA
21

22. DAR EL PROBLEMA Y EL ESQUEMA PARA QUE COLOQUEN
EN ÉL LOS DATOS CORRESPONDIENTES
-En mi equipo de fútbol llevamos marcados 33
goles. Si en el próximo partido conseguimos meter
6 goles, ¿cuántos goles habremos marcado en
total?
22 APLICACIÓN

23. DADO UN PROBLEMA
COMPLETAR EL ESQUEMA
•María y su hermano cuentan sus juguetes. Entre
los dos tienen 12 juguetes. El hermano de María
tiene 5 juguetes. ¿Cuántos juguetes tiene Begoña?
23
0 5

24. RELACIÓN ENTRE OPERACIONES,
ESQUEMAS Y TEXTOS DE PROBLEMAS
•LEE EL PROBLEMA Y RODEA LA OPERACIÓN QUE LO
RESUELVE
-En una canasta hay 16 manzanas y 9 peras. Tres de
las manzanas están podridas y las tiro a la basura.
Cuántas frutas quedarán en la canasta?
16 – 9 – 3 16 – 3 + 9
16 + 9 + 3
24

25. •COMPLETA EL TEXTO DEL PROBLEMA. TEN EN CUENTA EL ESQUEMA
- Tenía 8 canicas para jugar en el recreo y un agujero en el bolsillo del pantalón.
........................................................................................................................
....
¿.........................................................................................................................?
CEP DE CASTILLEJA DE LA
CUESTA
25
?
8
5

26. Estrategias heurísticas para el III ciclo
a. Realizar una simulación: consiste en representar el problema de forma
vivencial y con material concreto.
b. Hacer un diagrama: implica realizar representaciones gráficas (icónicas,
pictóricas y simbólicas) en las que se relacionen los datos o elementos del
problema.
c. Usar analogías: implica comparar o relacionar los datos o elementos de un
problema, generando razonamientos para encontrar la solución por
semejanzas.
d. Ensayo y error: consiste en tantear un resultado y comprobar si puede ser la
solución del problema. Si la comprobación es correcta, se habrá resuelto el
problema, de otra forma, se continúa con el proceso.
e. Buscar patrones: consiste en encontrar regularidades en los datos del
problema y usarlas en la solución de problemas.
f. Hacer una lista sistemática: consiste en realizar una lista con los elementos
del problema para identificar datos y relacionarlos.
g. E mpezar por el final: consiste en resolver problemas en los que conocemos
el resultado final del cual se partirá para hallar el valor inicial.

27. • Realizar una simulación:
• Hacer un diagrama:

38. ¿Cuándo decimos que un niño o niña a
llegado a desarrollar la idea de suma o
resta?
Entre el segundo y tercer grado, los niños y las
niñas deben hacer que sus diversas estrategias
sean intercambiables pudiéndose aplicar a
todo tipo de problemas. En ese momento
podemos decir que ha llegado a “unificar” la
idea de suma o resta.

39. Conclusiones para la enseñanza
Cuatro elementos claves:
• Planteamiento de problemas diversos (PAEV)
• Aplicación de estrategias (Intercambiabilidad de
estrategias y memorización de hechos numéricos)
• Construcción de formas de representación (respetar
los ritmos de representación de los niños y postergar
lo más que se puede la introducción del signo +).
• Todo dentro del enfoque de la enseñanza de la
matemática a partir de la RP.