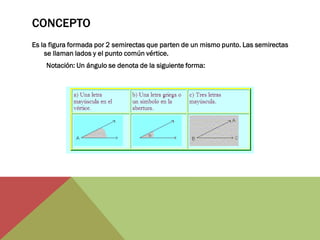
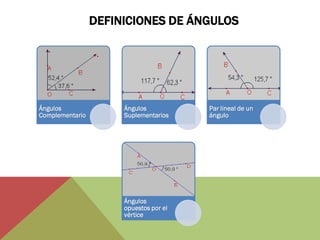
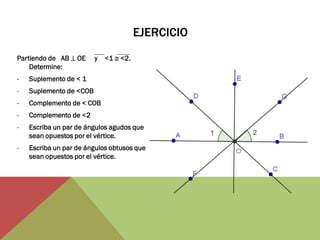
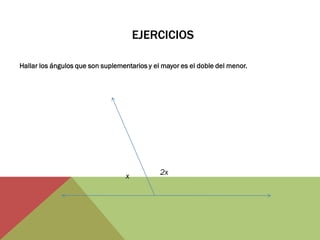
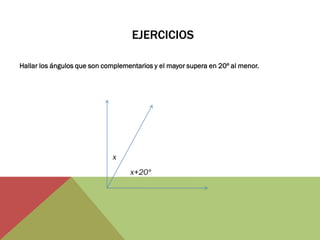
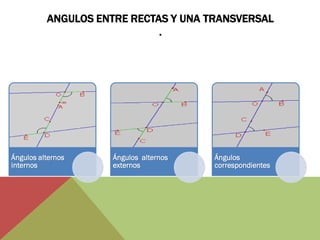
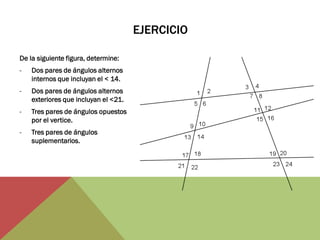
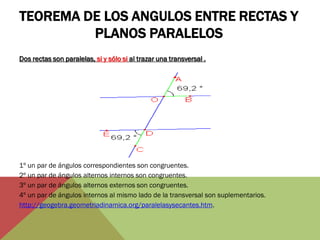
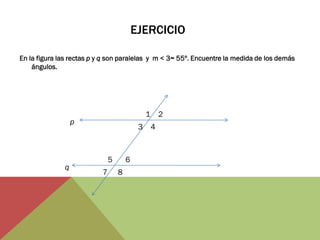
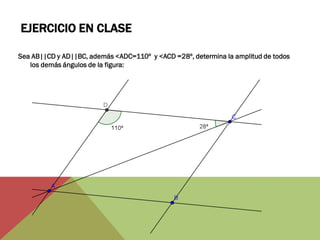
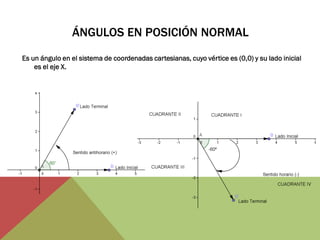
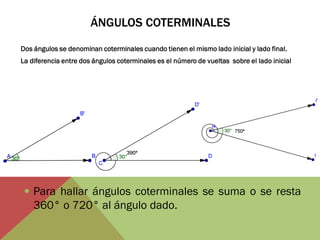
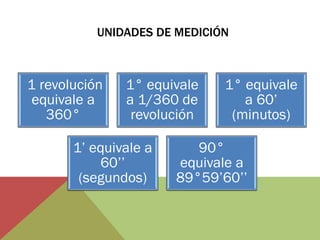
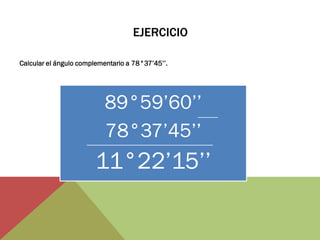
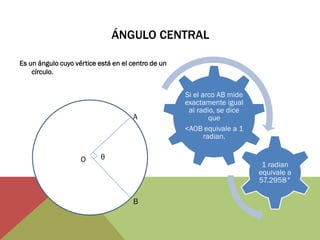
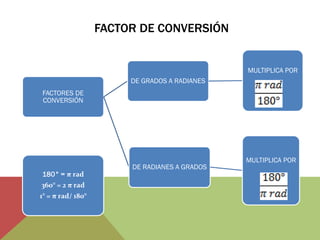
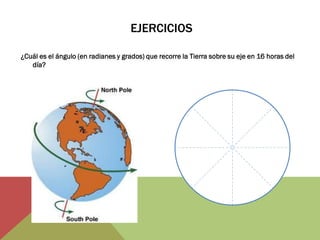
El documento habla sobre ángulos y diferentes tipos como complementarios, suplementarios y entre rectas paralelas. Explica definiciones, ejemplos y ejercicios sobre hallar ángulos dados otros datos como su medida u otros ángulos relacionados. También cubre conversiones entre grados, minutos, segundos y radianes.

2. CONCEPTO
Es la figura formada por 2 semirectas que parten de un mismo punto. Las semirectas se llaman lados y el punto común vértice.
Notación: Un ángulo se denota de la siguiente forma:

3. DEFINICIONES DE ÁNGULOS
Ángulos Complementario
Ángulos Suplementarios
Par lineal de un ángulo
Ángulos opuestos por el vértice

4. EJERCICIO
Partiendo de AB  OE y <1  <2. Determine:
-Suplemento de < 1
-Suplemento de <COB
-Complemento de < COB
-Complemento de <2
-Escriba un par de ángulos agudos que sean opuestos por el vértice.
-Escriba un par de ángulos obtusos que sean opuestos por el vértice.

5. EJERCICIOS
Hallar los ángulos que son suplementarios y el mayor es el doble del menor.
x
2x

6. EJERCICIOS
Hallar los ángulos que son complementarios y el mayor supera en 20º al menor.
x
x+20º

7. ANGULOS ENTRE RECTAS Y UNA TRANSVERSAL .
Ángulos alternos internos
Ángulos alternos externos
Ángulos correspondientes

8. EJERCICIO
De la siguiente figura, determine:
-Dos pares de ángulos alternos internos que incluyan el < 14.
-Dos pares de ángulos alternos exteriores que incluyan el <21.
-Tres pares de ángulos opuestos por el vertice.
-Tres pares de ángulos suplementarios.

9. TEOREMA DE LOS ANGULOS ENTRE RECTAS Y PLANOS PARALELOS
Dos rectas son paralelas, si y sólo si al trazar una transversal .
1º un par de ángulos correspondientes son congruentes.
2º un par de ángulos alternos internos son congruentes.
3º un par de ángulos alternos externos son congruentes.
4º un par de ángulos internos al mismo lado de la transversal son suplementarios.
http://geogebra.geometriadinamica.org/paralelasysecantes.htm.

10. EJERCICIO
En la figura las rectas p y q son paralelas y m < 3= 55º. Encuentre la medida de los demás ángulos.
2
1
3
4
5
7
6
8
p
q

11. EJERCICIO EN CLASE
Sea AB||CD y AD||BC, además <ADC=110º y <ACD =28º, determina la amplitud de todos los demás ángulos de la figura:

12. ÁNGULOS EN POSICIÓN NORMAL
Es un ángulo en el sistema de coordenadas cartesianas, cuyo vértice es (0,0) y su lado inicial es el eje X.

13. ÁNGULOS COTERMINALES
Dos ángulos se denominan coterminales cuando tienen el mismo lado inicial y lado final.
La diferencia entre dos ángulos coterminales es el número de vueltas sobre el lado inicial
Para hallar ángulos coterminales se suma o se resta 360° o 720° al ángulo dado.

14. EJERCICIO
Verifique si los ángulos 140° y 860° son coterminales.
Determine si -285° y -1365° son coterminales.

15. UNIDADES DE MEDICIÓN
1 revolución equivale a 360°
1° equivale a 1/360 de revolución
1° equivale a 60’ (minutos)
1’ equivale a 60’’ (segundos)
90° equivale a 89°59’60’’

16. EJERCICIO
Calcular el ángulo complementario a 78°37’45’’.
89°59’60’’
78°37’45’’
11°22’15’’

17. EJERCICIO
Calcular el ángulo suplementario a 78°37’45’’.
179°59’60’’
78°37’45’’
101°22’15’’

18. ÁNGULO CENTRAL
Es un ángulo cuyo vértice está en el centro de un círculo.
θ
A
B
O
Si el arco AB mide exactamente igual al radio, se dice que
<AOB equivale a 1 radian.
1 radian equivale a 57.2958°

19. FACTOR DE CONVERSIÓN
FACTORES DE CONVERSIÓN
DE GRADOS A RADIANES
MULTIPLICA POR
DE RADIANES A GRADOS
MULTIPLICA POR
180° = π rad
360° = 2 π rad
1° = π rad/ 180°

20. EJERCICIOS
¿Cuántos minutos en el reloj corresponden a un ángulo de 3π/ 4 rad?

21. EJERCICIOS
¿Cuál es el ángulo (en radianes y grados) que recorre la Tierra sobre su eje en 16 horas del día?

22. OTROS ENLACES
http://www.i- matematicas.com/recursos0809/1ciclo/angulosrectas/interactivo/Angulos.htm
http://mimosa.pntic.mec.es/clobo/geoweb/recta3.htm
http://es.scribd.com/doc/33029191/angulos-entre-paralelas
http://es.scribd.com/doc/33029843/angulos-alternativas