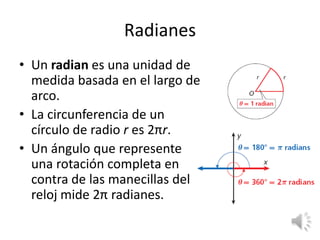
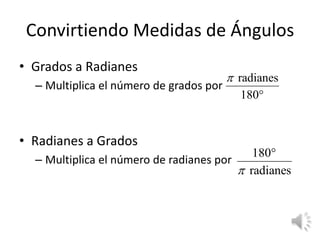
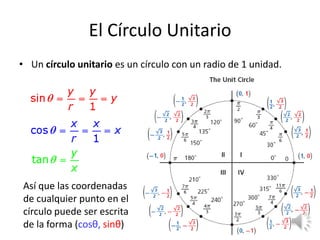
Este documento presenta varios ejercicios y conceptos sobre funciones trigonométricas y ángulos. Explica cómo convertir entre grados y radianes, encontrar valores de funciones trigonométricas usando el círculo unitario, y determinar ángulos de referencia para evaluar funciones trigonométricas. El objetivo es practicar la conversión de unidades de ángulo y el cálculo de funciones trigonométricas.

1. El Círculo UnitarioMatemática AvanzadaMI PROFESOR.Blog

2. Ejercicios PropuestosEncuentra la medida del ángulo de referencia para cada ángulo dado.120°225°-150°315°Encuentra el valor exacto de cada función trigonométrica.sen 60°tan 45°cos 45°cos 60°

3. ObjetivosConvertir medidas de ángulos entre grados y radianes.Encontrar el valor de funciones trigonométricas en el círculo unitario.

4. RadianesUn radian es una unidad de medida basada en el largo de arco.La circunferencia de un círculo de radio r es 2πr.Un ánguloquerepresenteunarotacióncompleta en contra de lasmanecillas del relojmide2πradianes.

5. Convirtiendo Medidas de ÁngulosGrados a RadianesMultiplica el número de grados porRadianes a GradosMultiplica el número de radianes por

6. Convirtiendo entre Grados y RadianesConvierte cada medida de grados a radianes o de radianes a grados.-45°80°-36°4πradianes

7. El Círculo UnitarioUn círculo unitario es un círculo con un radio de 1 unidad.Así que las coordenadas de cualquier punto en el círculo puede ser escrita de la forma (cosθ, sinθ)

8. Utilizando el Círculo Unitario para Evaluar Funciones TrigonométricasUtiliza el círculo unitario para encontrar el valor exacto de cada función trigonométrica.cos 210°tan 5π/3sen 225°tan 5π/6

9. Funciones Trigonométricas y Ángulos de ReferenciaPara encontrar el seno, coseno de θ:Determina la medida del ángulo de referencia de θ.Utiliza el cuadrante I del círculounitarioparaencontrar el seno, coseno o tangente del ángulo de referencia.Determina el cuadrante del lado terminal de θ en posiciónestándar. Ajusta el signo de seno, coseno o tangentebasado en el cuadrante del lado terminal.TODOS SIN TACOS

10. Utilizando Ángulos de Referencia para Evaluar Funciones TrigonométricasUtiliza un ángulo de referencia para encontrar el valor exacto del seno, coseno y tangente de cada ángulo.225°11π/6330°

11. FIN