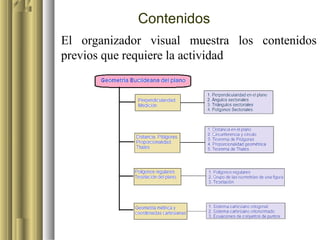
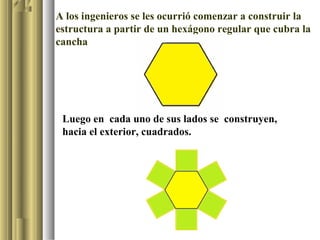
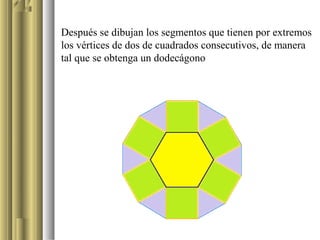
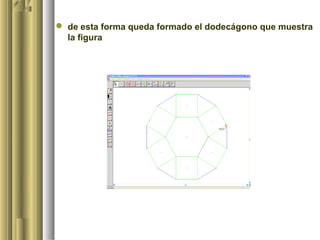
Este documento describe una actividad educativa en la que los alumnos de tercer año de secundaria aplican y analizan las propiedades de los polígonos regulares mediante el software Cabri II Plus. Se centra en la construcción de un dodecágono a partir de un hexágono, utilizando herramientas gráficas para validar propiedades geométricas. La actividad busca que los estudiantes alcancen niveles de comprensión geométrica de acuerdo a la teoría de van Hiele.

1. Matemática:
Actividades de aplicación de
Polígonos Regulares
Dirigido a alumnos de tercer año de ciclo básico
de
Educación Segundaria
Prof. Lic. Nora E. Herrera,
e-mail nora_edith_herrera@gmail.com

2. Objetivo
El propósito de esta actividad es que los
alumnos sean capaces de aplicar y
analizar las propiedades de los polígonos
regulares, con la ayuda de un software
educativo (Cabri II Plus ).
Dirección del software
http://www.cabri.com/es/descargar-cabri-2-plus.html

3. Contenidos
El organizador visual muestra los contenidos
previos que requiere la actividad

4. Introducción
 El Estadio del Bicentenario de San Juan, es un
estadio multipropósito ubicado, al sur de la Ciudad
de San Juan, al norte del departamento Pocito, en la
provincia de San Juan, Rep. Argentina. Su
inauguración se produjo el día 16 de marzo de 2011.
Es utilizado principalmente para partidos de fútbol
y fue una de las de las sedes del Campeonato de la
Copa América 2011.

5. Actividad
 El Gobierno de San Juan llamó a licitación a
empresas locales para la construcción del
techo del nuevo estadio de fútbol.
Finalizada la licitación, la empresa a la que
se le adjudicó la obra propuso construir
una estructura de forma de dodecágono.

6. A los ingenieros se les ocurrió comenzar a construir la
estructura a partir de un hexágono regular que cubra la
cancha
Luego en cada uno de sus lados se construyen,
hacia el exterior, cuadrados.

7. Después se dibujan los segmentos que tienen por extremos
los vértices de dos de cuadrados consecutivos, de manera
tal que se obtenga un dodecágono

8. 1- ¿Es la estructura del techo, un
dodecágono regular? Justifique su
respuesta
2- ¿Cuántos metros cuadrados de toldo
para techos se necesitan comprar, si el
lado del hexágono inicial con el que se
comienza a construir la estructura del
techo, mide 40 m?
Sugerencia: cuando trabaje con el software, Cabri II Plus use la
unidad milímetros en vez de la unidad real, es decir metros, ya que
sería imposible trabajar en metros en la pantalla de su computadora
 A continuación se muestra como resolver el items 1-
de la actividad.

9. Respuesta para el item 1-
Para que sea regular se debe verificar:
Todos sus ángulos miden lo mismo. En
este caso como la figura es un
dodecágono, sus ángulos interiores
deben medir 150°
Todos sus lados son congruentes (y
congruentes a los lados del hexágono
regular)

10. Resolución con Cabri 2 plus
 Primero con la herramienta polígono regular
se grafica el hexágono con el que parten los
ingenieros para crear la estructura del techo.
Luego siguiendo los pasos del problema se deben
construir, usado esa herramienta, los cuadrados a
partir de cada uno de los seis lados del hexágono.
 Una vez graficados los cuadrados, se procede a unir
con segmentos los vértices de los cuadrados
consecutivos, mediante con la herramienta segmento

11.  de esta forma queda formado el dodecágono que muestra
la figura

12.  Por último como se quiere saber cual es la medida del
ángulo interior del dodecágono, se procede a utilizar la
herramienta medir ángulo
Esta herramienta permite observar cual es la medida de
todos los ángulos interiores del dodecágono, y así ver
que todos los ángulos del dodecágono son congruentes.
También, permite analizar que los triángulos formados
por dos lados de cuadrados consecutivos son isósceles
y que sus ángulos interiores miden 60°, por lo tanto es
un triángulo equilátero. Luego todos los lados del
dodecágono miden lo mismo.
Por lo tanto se puede concluir que es un dodecágono
regular.

13. Finalidad
Mediante esta actividad, los alumnos alcanzan el
nivel 3, de la teoría de los Van Hiele, en efecto
para resolverla deben:
 reconocer segmentos, hexágonos,
cuadriláteros y dodecágonos, por su forma
(nivel 1. reconocimiento)
 analizar las propiedades de las figuras, para
graficar figuras regulares (nivel 2. análisis)
 ordenar de manera lógica las propiedades de
los triángulos, hexágonos, cuadriláteros y
dodecágonos para determinar si son polígonos
regulares (nivel 3. ordenamiento)

14. Referencias bibliográficas
 http://es.wikipedia.org/wiki/Estadio_San_Juan_
del_Bicentenario. Recuperado 11-03-13
 http://www.google.com.ar/imgres?
q=estadio+del+bicentenario&hl=es&sa=X&rlz=1
R2ADFA_esAR423&tbm=isch&prmd=imvns&tb
nid=6VX1VGuuG81tYM:&imgrefurl=http://www.t
aringa.net/posts/deportes/9969853/Los-
mejores-estadios-de-Argentina. Recuperado
fecha 11-03-13
 Alderete, M. J. y cols (2009) Geometrías
Kleinianas. Mendoza: FEEYE. e – book