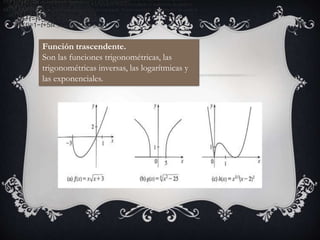
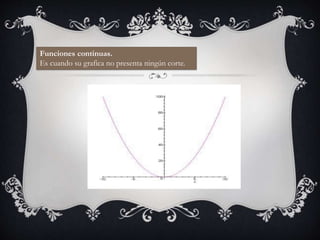
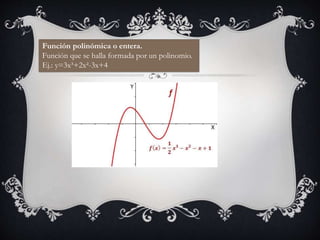
El documento resume diferentes tipos de funciones matemáticas como funciones algebraicas, inyectivas, trascendentes, crecientes, decrecientes, continuas, discontinuas, polinómicas, potenciales e inversas. Proporciona ejemplos de cada tipo de función.

1. Sánchez Vázquez Alberto
5to semestre Grupo B
Turno Matutino
Calculo Diferencial
Profesor Erasmo
Escuela Preparatoria Oficial
Epo 122

2. Función algebraica.
Son aquellas donde aparecen las operaciones
de suma, resta, multiplicación, división,
potenciación y radicación.
Ej.: y=(√3x+5)/(7x³-12)

3. Función inyectiva.
También llamada función uno a uno, se
caracteriza porque a cada preimagen x є A,
le corresponde una y solo una imagen y є B,
lo cual se resume en: si X1 ≠ X2, entonces
f(X1) ≠ f(X2) para todo X1 y X2 en el
dominio

4. Función trascendente.
Son las funciones trigonométricas, las
trigonométricas inversas, las logarítmicas y
las exponenciales.
h(x)=1+x1−x√ , es una función algebraica.
u(t)=1−t+5t4 , es un polinomio de grado 4.
g(x)=x50 , es una función potencia (la x es la base$. Podrìa considerar un polinomio de grado 5.
h(x)=1+x1−x√ , es una función algebraica.
u(t)=1−t+5t4 , es un polinomio de grado 4.
g(x)=x50 , es una función potencia (la x es la base$. Podrìa considerar un polinomio de grado 5.
h(x)=1+x1−x√ , es una función algebraica.
u(t)=1−t+5t4 , es un polinomio de grado 4.
f(x)=5x , es una función exponencial (La x es la exponente).
g(x)=x50 , es una función potencia (la x es la base$. Podrìa considerar un polinomio de grado 5.
h(x)=1+x1−x√ , es una función algebraica.
u(t)=1−t+5t4 , es un polinomio de grado 4.

5. . Función creciente.
Una función f es creciente sobre un intervalo
(rango de dos valores perteneciente a los reales
tales que uno es mayor que otro) en R si, para
cualquier X1 y X2 en R, donde X1 < X2, se tiene
que f(X1) < f(X2), es decir, los valores de
función se incrementan

6. Función decreciente.
Una función f es decreciente sobre un intervalo
en R si, para cualquier X1 y X2 enR, donde
X1>X2, se tiene que f(X1) > f(X2), es decir, los
valores de función disminuyen.

7. Funciones continuas.
Es cuando su grafica no presenta ningún corte.

8. Funciones discontinuas.
Cuando su grafica presenta al menos un corte

9. Función polinómica o entera.
Función que se halla formada por un polinomio.
Ej.: y=3x³+2x²-3x+4

10. Función potencial.
Función que contiene potencias de la variable x,
en donde x se halla elevada a una constante.
Ej.: y=[3x+2]³

11. Función inversa.
Si f es una función que tiene por dominio al
conjunto A y por rango al conjunto B, entonces
se llama la función inversa de f, aquella que tiene
por dominio el conjuntoB y por rango al
conjunto A.