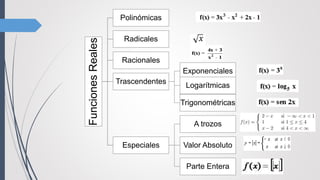
Este documento clasifica y describe diferentes tipos de funciones, incluyendo funciones polinómicas, radicales, racionales y trascendentes. Describe funciones constantes, afines y potencia, así como funciones radicales como raíz cuadrada y cúbica. Explica cómo el dominio y recorrido de estas funciones dependen de los parámetros de la función, y cómo se ven afectadas por traslaciones en los ejes x e y.



![Función Potencia (Exponente Par)
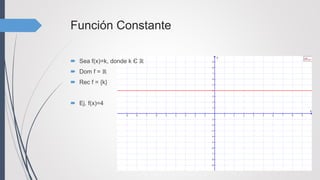
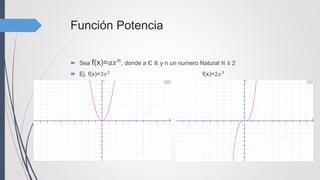
Dom f= ℝ
El Rec f depende del valor de a
Si a>0 Rec f= [0;+∞) Si a<0 Rec f= (-∞;0]](https://image.slidesharecdn.com/clasificacindefunciones-160601130808/85/Clasificacion-de-funciones-7-320.jpg)
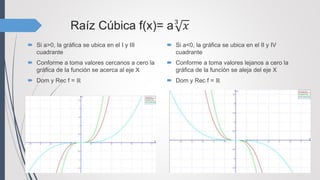
![Función Potencia (Exponente Impar)
Dom f= ℝ
El Rec f= ℝ
Si a>0, gráfica en cuadrantes(I y III) Si a<0 Rec f= (-∞;0] gráfica en cuadrantes(II y IV)](https://image.slidesharecdn.com/clasificacindefunciones-160601130808/85/Clasificacion-de-funciones-8-320.jpg)
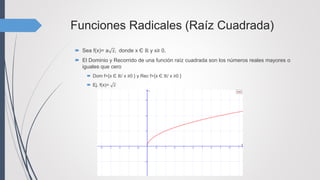
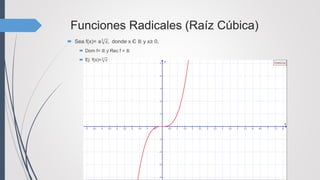
![Raiz Cuadrada f(x)= a 𝑥
Si a>0, la gráfica se ubica en el primer
cuadrante
Conforme a toma valores cercanos a cero la
gráfica de la función se acerca al eje X
Dom f= [0;+∞) Rec f = [0;+∞)
Si a<0, la gráfica se ubica en el cuarto
cuadrante
Conforme a toma valores lejanos a cero la
gráfica de la función se aleja del eje X
Dom f= [0;+∞) Rec f = (-∞;0]](https://image.slidesharecdn.com/clasificacindefunciones-160601130808/85/Clasificacion-de-funciones-10-320.jpg)
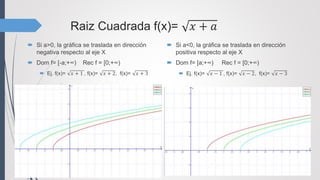
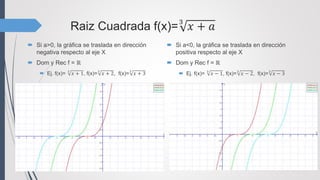
![Raiz Cuadrada f(x)= 𝑥 +a
Si a>0, la gráfica se traslada en dirección
positiva respecto al eje Y
Dom f= [0;+∞) Rec f = [a;+∞)
Ej. f(x)= 𝑥 + 1, f(x)= 𝑥+2, f(x)= 𝑥 + 3
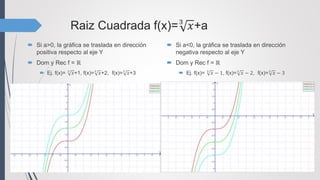
Si a<0, la gráfica se traslada en dirección
negativa respecto al eje Y
Dom f= [0;+∞) Rec f = (a ;+∞]
Ej. f(x)= 𝑥 − 1, f(x)= 𝑥 −2, f(x)= 𝑥 − 3](https://image.slidesharecdn.com/clasificacindefunciones-160601130808/85/Clasificacion-de-funciones-12-320.jpg)