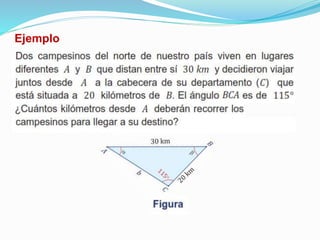
El documento detalla las funciones matemáticas, incluyendo constantes, lineales, cuadráticas, exponenciales y logarítmicas, así como sus propiedades, dominios y rangos. También se abordan identidades y ecuaciones trigonométricas, incluyendo la ley de los senos y cosenos. Se ilustran ejemplos de graficación y análisis de diferentes tipos de funciones.






![Ejemplos: Escribir dominio, rango y graficar cada función.
𝒚 = 𝟐𝒙 + 𝟑
𝑦
0 𝑥
(1, 5)5
(0, 3)
1 2
2) 𝒈 𝒙 = − 𝒙 + 𝟐, 𝒙 ∈ [−𝟏, 𝟒)1)𝒇(𝒙) = 𝟐𝒙 + 𝟑
𝐷𝑜𝑚 𝑓 = ℝ
𝑅𝑎𝑛 𝑓 = ℝ
𝐷𝑜𝑚 𝑓 = [−1, 4)
𝑅𝑎𝑛 𝑓 = (−2, 3]
(4, −2)
(−1, 3)
𝒚 = − 𝒙 + 𝟐, 𝒙 ∈ [−𝟏, 𝟒)
𝑦
0 𝑥
4−1
−2
3
°](https://image.slidesharecdn.com/resumendefunciones-151124195420-lva1-app6892/85/Repaso-de-Funciones-8-320.jpg)
![Función Cuadrática
Una función cuadrática tiene la forma
𝑦 = 𝑎 𝑥 – 𝑏 2
+ 𝑐, 𝑎, 𝑏, 𝑐 ∈ 𝑅 , 𝑎 ≠ 0.
Dominio: ℝ
Rango: (−, 𝑐] si 𝑎 < 0 y [𝑐, +) si 𝑎 > 0.
La gráfica de una función cuadrática es una curva
llamada parábola y tiene vértice 𝑉(𝑏, 𝑐).
El eje de simetríade la parábola es la recta vertical que
divide a esta en dos partes iguales.](https://image.slidesharecdn.com/resumendefunciones-151124195420-lva1-app6892/85/Repaso-de-Funciones-9-320.jpg)