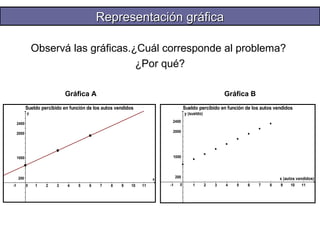
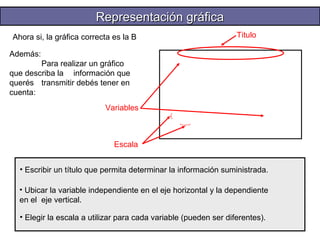
El documento presenta información sobre funciones matemáticas. Explica que una función es una correspondencia entre dos conjuntos donde a cada elemento del primer conjunto le corresponde un único elemento del segundo conjunto. Describe diferentes tipos de funciones como lineales, cuadráticas, de proporcionalidad directa e inversa, y exponenciales. También incluye un ejemplo numérico sobre el sueldo de un vendedor que depende de la cantidad de autos vendidos.

1. MMAATTEEMMÁÁTTIICCAASS
FFUUNNCCIIOONNEESS

2. FFUUNNCCIIOONNEESS
• Definición de función.
• Representación gráfica
• Clasificación de funciones
• Ceros de una función
x
y

3. FFuunncciioonneess
Las funciones constituyen una herramienta
útil para describir, analizar e interpretar
diversas situaciones provenientes de la
Matemática y de otras ciencias.
Permiten expresar relaciones entre variables
y construir modelos referidos a distintas
áreas (biología, economía, física, etc.).

4. ¿Qué es una función?
Esta unidad te presenta un nuevo desafío: el estudio de funciones.
Seguramente tendrás alguna idea sobre este tema estudiado en la escuela.
y
x
yy
x
¿Función?
f(x) = x - 4
f(x) = x2 + 3
FFuunncciioonneess

5. Para pensar…
Ud. es seleccionado para trabajar como vendedor en una
concesionaria de automóviles. En la entrevista se
acuerdan las condiciones del trabajo, beneficios que se le
otorgan y la forma en que se compone el sueldo.
Cada vendedor recibe un sueldo fijo de $700 y $200
adicionales por cada automóvil vendido. El número
máximo de unidades a vender por cada vendedor es de 8 y
si se presenta la oportunidad de una nueva venta, a partir
de la octava, deberá cederla a otro vendedor.
¿Qué sueldo recibirá si vende 6 automóviles?
¿Y si no realiza ninguna venta?
$700 + 6 . $200 = $1900
¿Y si vende 3 automóviles? $700 + 3 . $200 = $1300
$700
¿Y si vende x automóviles? y = $700 + $200. x
Fórmula
FFuunncciioonneess

6. FFuunncciioonneess
Los datos obtenidos se pueden
organizar en una tabla de valores donde
y = 700 + 200 x
x y
6
3
0
…
1900
1300
700
…
Puedes observar que:
“a cada vendedor de la agencia se le asigna
un único sueldo en el mes”, quedando el
mismo determinado por la cantidad de
vehículos vendidos.
Cada mes, tu sueldo puede variar,¿de qué depende esa variación?
El sueldo depende de la cantidad de vehículos vendidos
Por lo tanto estás relacionando en cada caso dos variables:
número de autos vendidos variable independiente (x)
sueldo que le corresponde variable dependiente (y)

7. RReepprreesseennttaacciióónn ggrrááffiiccaa
Observá las gráficas.¿Cuál corresponde al problema?
¿Por qué?
Gráfica A Gráfica B
Sueldo percibido en función de los autos vendidos
2400
2000
1000
-1 1 2 3 4 5 6 7 8 9 10 11
x
y
200
0
Sueldo percibido en función de los autos vendidos
x (autos vendidos)
y (sueldo)
2400
2000
1000
200
0
-1 1 2 3 4 5 6 7 8 9 10 11

8. VVaarriiaabblleess
¿Qué valores puede tomar la variable x?
Pensá: ¿Puede venderse 2,7 autos? ¿Y 10 autos?
NO, solo pueden venderse 0, 1, 2, 3, 4, 5, 6, 7, 8 autos
¿Qué valores puede tomar la variable y?
Piensa:¿Puede percibir un sueldo de $600, trabajando en esa agencia?
NO, los sueldos posibles son 700, 900, 1100, 1300, 1500, 1700, 1900, 2100, 2300

9. Titulo
RReepprreesseennttaacciióónn ggrrááffiiccaa
Ahora si, la gráfica correcta es la B
Variables
Escala
Además:
Para realizar un gráfico
que describa la información que
querés transmitir debés tener en
cuenta:
• Escribir un título que permita determinar la información suministrada.
• Ubicar la variable independiente en el eje horizontal y la dependiente
en el eje vertical.
• Elegir la escala a utilizar para cada variable (pueden ser diferentes).

10. FFuunncciióónn:: ddeeffiinniicciióónn
Llegamos de esta manera a formalizar la definición de función
Se llama función del conjunto A en el conjunto B ( f : A  B ) a toda
correspondencia entre los elementos de ambos conjuntos, de modo que a
todo elemento del conjunto A le corresponde un único elemento del
conjunto B.
El conjunto A es el dominio de la función y el conjunto B el codominio
x y = 700 + 200 x
6
1900
3
1300
0
700
1
900
2
1100
4
1500
5
1700
7
2100
8
2300
f(6) = 1900, es decir:
1900 es la imagen de 6 o 6 es la pre-imagen de 1900
Además: f(6) es el sueldo que cobrará si vende 6 autos
Si se designa con x a los elementos del conjunto A
y con y a los elementos del conjunto B, la relación
entre las variables la simbolizamos:
y = f(x), y = g(x), y = s(x), etc.
donde f, g, s, … es el nombre de la función
y es la imagen de x y x es la pre-imagen de y
Observa

11. CCllaassiiffiiccaacciióónn ddee ffuunncciioonneess
Funciones
Lineales
Cuadráticas
De proporcionalidad directa
De proporcionalidad inversa
Exponencial
• Función lineal: es toda función cuya fórmula sea de la forma y = a x
+ b
Su gráfica es una recta: a es la pendiente y b es la ordenada al origen.
b = 0, es de proporcionalidad directa.
a = 0, una función constante.
•Función cuadrática, se expresa y = a . x² + b . x + c
Su gráfica es una curva llamada parábola. Cada parábola tiene un eje
de simetría paralelo al eje de las ordenadas, y un vértice que es el
punto del eje de simetría que pertenece a la curva.

12. • De proporcionalidad directa: toda función que sea de la forma
y = k . x (k distinto a 0)
Las gráficas de estas funciones son rectas que contienen al origen
de coordenadas.
El número k es la constante de proporcionalidad y gráficamente
está asociado a la inclinación de la recta.
• De proporcionalidad inversa: toda función cuya expresión sea de
la forma y = k/x (k es un número real; x distinto a 0 y k distinto a 0)
Los puntos de su gráfica están sobre una curva llamada hipérbola,
que no tiene contacto con los ejes cartesianos.
• Exponencial: toda función cuya expresión sea de la forma y = k .
ax, (k y a son números reales, a mayor a 0, y a distinto a 1). Los
puntos de su gráfica pertenecen a una curva que no tiene contacto
con el eje de las x.

13. FFuunncciioonneess
Llegó el momento de practicar lo aprendido