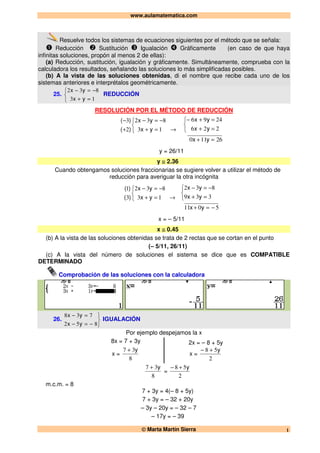
Este documento presenta la resolución de varios sistemas de ecuaciones por diferentes métodos como reducción, sustitución, igualación y gráficamente. Explica cada método con ejemplos numéricos y da las soluciones de cada sistema, indicando si son compatibles determinados, incompatibles o tienen infinitas soluciones.