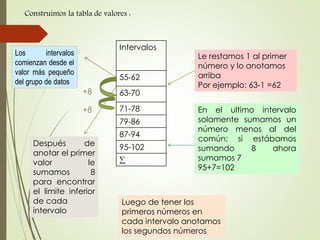
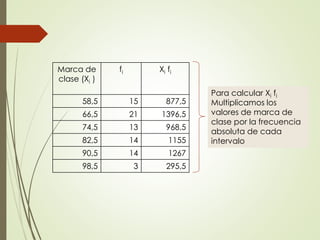
Este documento presenta los pasos para resolver un ejercicio estadístico que incluye calcular el rango, construir una tabla de frecuencias e intervalos, y determinar la media, moda y mediana. Primero se calcula el rango como el valor mayor (97) menos el menor (55), dando un rango de 42. Luego se dividen los datos en 6 intervalos de 8 datos cada uno y se construye la tabla de frecuencias. Finalmente, se calcula la media como la suma de los productos de las marcas de clase por sus frecuencias dividido entre el total de datos

1. ESTADÍSTICA

2. EJERCICIO
Del siguiente ejercicio:
a) Determine el rango
b) Calcule el valor de los intervalos tomando en cuenta el número de datos
c) Construya la tabla de valores
d) Defina la media, moda y mediana

3. 55 64 62 70 56 56 70 90 80 82
81 60 62 65 80 92 97 58 65 81
78 76 80 82 74 58 69 74 77 77
59 60 65 66 89 90 87 75 58 62
68 69 90 95 87 89 85 84 70 68
63 63 69 71 76 74 86 88 90 95
88 64 66 86 75 70 60 88 92 81
63 62 64 70 68 72 75 80 84 88
- En una prueba aplicada a 80 estudiantes para determinar el nivel de inglés,
se obtuvieron los siguientes resultados sobre 100 puntos

4. Primero determinamos el mayor y el menor valor de los datos que
tenemos
55 64 62 70 56 56 70 90 80 82
81 60 62 65 80 92 97 58 65 81
78 76 80 82 74 58 69 74 77 77
59 60 65 66 89 90 87 75 58 62
68 69 90 95 87 89 85 84 70 68
63 63 69 71 76 74 86 88 90 95
88 64 66 86 75 70 60 88 92 81
63 62 64 70 68 72 75 80 84 88
Rojo: Valor Mayor
Azul: Valor Menor
Para resolver el ejercicio:

5. a) Para determinar el rango
- Restamos el valor mayor con el valor menor
97-55= 42
- Tomamos los valores señalados anteriormente
Valor mayor: 95 Valor menor:55
Rango: 42
Ese sería el resultado

6. b) Calcule el valor de los intervalos tomando en cuenta el
número de datos
- Tomamos el valor del rango calculado anteriormente y le sumamos 1
=42+1
=43
- Este valor lo dividimos por el numero de intervalos que sean
necesarios
Para saber cuál es el número de intervalos aplicamos el siguiente
criterio :
 Entre 1 y 50 datos = 6 intervalos
 Entre 51 y 100 datos = 7 intervalos
 Entre 101 y 500 datos = 8 intervalos
 Entre 501 y 1000 datos = 9 intervalos
 Entre 1001 y 1500 datos = 10 intervalos
 De 1501 datos hacia adelante = 15 intervalos

7. Como tenemos 43 datos utilizamos 6 intervalos
43/6= 7,1667
Entonces aproximamos el cociente al entero próximo
mayor
Por lo tanto tendremos 8 datos por
intervalo
- El siguiente paso es dividir estos 2 valores
* El número de datos por intervalo serían 7,1667; pero
estos no pueden ser números decimales, o fraccionarios,
solamente enteros

8. Construimos la tabla de valores :
Intervalos
55-62
63-70
71-78
79-86
87-94
95-102

Los intervalos
comienzan desde el
valor más pequeño
del grupo de datos
Después de
anotar el primer
valor le
sumamos 8
para encontrar
el limite inferior
de cada
intervalo
+8
+8
Luego de tener los
primeros números en
cada intervalo anotamos
los segundos números
Le restamos 1 al primer
número y lo anotamos
arriba
Por ejemplo: 63-1 =62
En el ultimo intervalo
solamente sumamos un
número menos al del
común; si estábamos
sumando 8 ahora
sumamos 7
95+7=102

9. Intervalos Marca de
clase (Xi )
55-62 58,5
63-70 66,5
71-78 74,5
79-86 82,5
87-94 90,5
95-102 98,5
La Marca de Clase es el promedio ente los dos
límites inferior y superior de un intervalo
Para calcular la media aritmética:
-Sumamos los dos limites del
intervalo
55+62=117
-Este resultado lo dividimos para 2
117/2=58,5

10. Conteo fi ni Fi Ni
||||||||
|||||||
15 0,1875 15 0,1875
||||||||
||||||||
|||||
21 0,2625 36 0,4500
||||||||
|||||
13 0,1625 49 0,6125
||||||||
||||||
14 0,1750 63 0,7875
||||||||
||||||
14 0,1750 77 0,9625
||| 3 0,0375 80 1,0
 80 1,0
fi Es el número de datos
que existen en cada
intervalo
Para calcular ni se divide fi
para la suma total de fi ( fi )
Es importante que los
decimales estén bien
aproximados para que su suma
total nos de 1
Para
calcular
Fi y Ni se van
sumando
los valores
de fi
y ni de
manera
vertical

11. Marca de
clase (Xi )
fi Xi fi
58,5 15 877,5
66,5 21 1396,5
74,5 13 968,5
82,5 14 1155
90,5 14 1267
98,5 3 295,5
Para calcular Xi fi
Multiplicamos los
valores de marca de
clase por la frecuencia
absoluta de cada
intervalo

12. Intervalos Conteo Marca de
clase (Xi )
fi ni Fi Ni Xi fi
55-62 |||||
|||||
|||||
58,5 15 0,1875 15 0,1875 877,5
63-70 |||||
|||||
|||||
|||||
|
66,5 21 0,2625 36 0,4500 1396,5
71-78 |||||
|||||
|||
74,5 13 0,1625 49 0,6125 968,5
79-86 |||||
|||||
||||
82,5 14 0,1750 63 0,7875 1155
87-94 |||||
|||||
||||
90,5 14 0,1750 77 0,9625 1267
95-102 ||| 98,5 3 0,0375 80 1,0 295,5
 80 1,0 5960
La tabla completa sería

13. Calcule la media aritmética
Para calcular la media
aritmética aplicamos la siguiente
fórmula:
N=fi
=
5960
80
= 74,5
En donde:
 Xi fi = sumatoria de la
multiplicación de marca de
clase por frecuencia absoluta
fi = sumatoria de
frecuencia absoluta
Resolviendo:

14. Calcule la moda
Mo= Li +
fi+1
fi−1 +fi+1
∗ ai
Para calcular la moda
aplicamos la siguiente fórmula:
En donde:
Li = limite inferior del intervalo modal
fi+1 = diferencia entre la frecuencia
modal y la frecuencia de clase
anterior
fi-1 = diferencia entre la frecuencia
modal y la frecuencia de clase
posterior
ai = ancho del intervalo modal

15. Para resolver:
Intervalos fi
55-62 15
63-70 21
71-78 13
79-86 14
87-94 14
95-102 3
Nos fijamos en el valor más alto
de fi
21 pertenece al intervalo de 63-70
por lo que Li =63
La frecuencia de clase anterior a 21
es 15 por lo que fi+1 = 6
La frecuencia de clase posterior a
21 es 13 por lo que fi-1 = 8
El ancho del intervalo modal (ai )
es 8
Resolviendo:
Mo=63+
6
8+6
∗ 8
Mo=63+
6
14
∗ 8
Mo=63+
6
14
∗ 8
Mo=63+3,43
Mo=66,43

16. Calcular la mediana
Para calcular la mediana
aplicamos la siguiente fórmula:
En donde:
Li = es el límite inferior de la clase donde se
encuentra la mediana.
𝑁
2
= es la semisuma de las frecuencias absolutas.
Fi-1 = es la frecuencia acumulada anterior a la clase
mediana.
ai = es la amplitud de la clase.

17. Intervalos fi Fi
55-62 15 15
63-70 21 36
71-78 13 49
79-86 14 63
87-94 14 77
95-102 3 80
Para calcular:
fi
2
=
80
2
= 40
Clase de la mediana : 71-78)
Me=71+
40−36
13
∗ 8
Me=71+2,46
Me=71+
4
13
∗ 8
Me=73,46