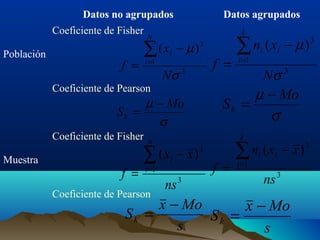
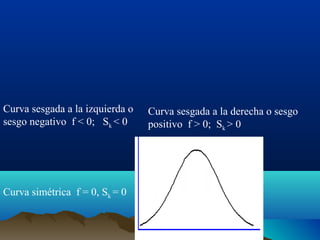
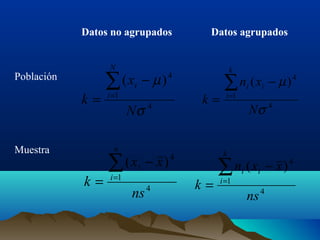
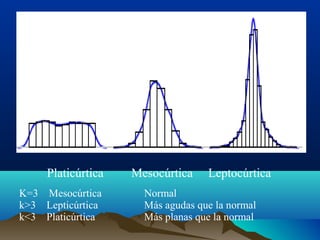
Este documento trata sobre medidas de dispersión y forma en estadística. Explica medidas de dispersión como el rango, rango intercuartílico, desviación media y varianza. También cubre medidas de forma como asimetría y curtosis. Define cada medida y proporciona fórmulas para calcularlas tanto para datos agrupados como no agrupados.

1. ESTADÍSTICA YESTADÍSTICA Y
PROBABILIDADESPROBABILIDADES
UNHEVAL- 2009UNHEVAL- 2009
Mg. VARGAS RONCAL, RosarioMg. VARGAS RONCAL, Rosario

2. CAPÍTULO IV. MEDIDAS DECAPÍTULO IV. MEDIDAS DE
DISPERSIÓN Y DE FORMADISPERSIÓN Y DE FORMA

3. 4.1 MEDIDAS DE DISPERSIÓN4.1 MEDIDAS DE DISPERSIÓN
• Se llaman medidas de dispersión aquellas que
permiten retratar la distancia de los valores de la
variable a un cierto valor central, o que permiten
identificar la concentración de los datos en un cierto
sector del recorrido de la variable. .

4. 4.1.1 RANGO O AMPLITUD ( R )4.1.1 RANGO O AMPLITUD ( R )
• Es la diferencia entre las medidas mayor y menor de un conjunto de
datos.
• Datos no agrupados
R = Xmax-Xmin Xmax: dato mayor Xmin: dato menor
• Datos agrupados
• R = Ls – Li Ls: límite mayor y Li: límite menor
• PROPIEDADES DEL RANGO
• Es fácil de calcular y sus unidades son las mismas que las de la
variable.
• No utiliza todas las observaciones (sólo dos de ellas);
• Se puede ver muy afectada por alguna observación extrema;
• El rango aumenta con el número de observaciones, o bien se
queda igual. En cualquier caso nunca disminuye.

5. 4.1.2 RANGO INTERCUARTÍLICO (RIQ).4.1.2 RANGO INTERCUARTÍLICO (RIQ).
• Lo calculamos como la diferencia entre el
tercero y el primero de los cuartiles.
• RIQ = q3 - q1, el intervalo [q1,q3] contiene al
50% central de los valores muestrales.

6. 4.1.3 DESVIACIÓN MEDIA (Dm)4.1.3 DESVIACIÓN MEDIA (Dm)
Es la media aritmética de todas las diferencias
absolutas entre cada observación individual y la
media aritmética del conjunto de datos.
Datos no agrupados Datos agrupados
Población
Muestra
u: media de la población ni: frecuencia de clase i
xi: punto medio de clase i ; n : total de observaciones
N
x
D
N
i
i
m
∑=
−
= 1
µ
N
xn
D
N
i
ii
m
∑=
−
= 1
µ
n
xx
D
n
i
i
m
∑=
−
= 1
n
xxn
D
n
i
ii
m
∑=
−
= 1

7. 4.1.4 VARIANZA (S4.1.4 VARIANZA (S22
))
Es la media aritmética del cuadrado de las
desviaciones de cada uno de los valores respecto a la
media.
Datos no agrupados Datos agrupados
Población
Muestra
K: número de intervalos
N
Nxn
k
i
ii
2
1
2
2
µ
σ
−
=
∑=
1
2
1
2
2
−
−
=
∑=
n
xnxn
s
k
i
ii
1
2
1
2
2
−
−
=
∑=
n
xnx
s
n
i
i
N
nx
N
i
i
2
1
2
2
µ
σ
−
=
∑=

8. 4.1.6 COEFICIENTE DE VARIACIÓN (CV)
Para comparar la dispersión de variables que aparecen en
unidades diferentes (metros, kilos, etc.) o que corresponden a
poblaciones extremadamente desiguales, es necesario disponer
de una medida de variabilidad que no dependa de las unidades
o del tamaño de los datos.
A menor coeficiente de variación consideraremos que la
distribución de la variable medida es más homogénea.
Población
Muestra
u
CV
σ
=
x
s
CV =

9. 4.2 MEDIDAS DE FORMA4.2 MEDIDAS DE FORMA
• La forma de una distribución de
frecuencias se puede describir por su
simetría o falta de ella (asimetría) y por su
agudeza (curtosis).

10. 4.2.1 ASIMETRÍA4.2.1 ASIMETRÍA
• Otro rasgo interesante en una distribución de frecuencias
es si los datos aparecen ubicados simétricamente o no
respecto de la media. Si queremos cuantificar la simetría,
es necesario conservar la información acerca tanto del
signo como de la distancia de cada dato a la media (centro
de simetría).
• En el caso en que el coeficiente valga cero la distribución
es simétrica alrededor de la media.
• Los valores positivos, indicarán distribuciones con mayor
sesgo a la derecha y los valores negativos indicarán un
mayor sesgo a la izquierda.

11. Datos no agrupados Datos agrupados
Población
Coeficiente de Fisher
Coeficiente de Pearson
Muestra
Coeficiente de Fisher
Coeficiente de Pearson
3
1
3
)(
σ
µ
N
x
f
N
i
i∑=
−
=
σ
µ Mo
Sk
−
=
3
1
3
)(
σ
µ
N
xn
f
k
i
ii∑=
−
=
s
Mox
Sk
−
=
3
1
3
)(
ns
xx
f
n
i
i∑=
−
= 3
1
3
)(
ns
xxn
f
k
i
ii∑=
−
=
s
Mox
Sk
−
=
σ
µ Mo
Sk
−
=

12. Curva sesgada a la derecha o sesgo
positivo f > 0; Sk > 0
Curva sesgada a la izquierda o
sesgo negativo f < 0; Sk < 0
Curva simétrica f = 0, Sk = 0

13. 4.2.2 CURTOSIS4.2.2 CURTOSIS
• Miden la mayor o menos concentración de
datos alrededor de la media. Se suele
medir con el coeficiente de curtosis, que
describe lo picuda o plana que es la
distribución, es decir si los datos se
concentran demasiado o no, comparados
con un modelo de distribución llamado
distribución normal.

14. Datos no agrupados Datos agrupados
Población
Muestra
4
1
4
)(
ns
xx
k
n
i
i∑=
−
=
4
1
4
)(
σ
µ
N
xn
k
k
i
ii∑=
−
=4
1
4
)(
σ
µ
N
x
k
N
i
i∑=
−
=
4
1
4
)(
ns
xxn
k
k
i
ii∑=
−
=

15. Platicúrtica Mesocúrtica Leptocúrtica
K=3 Mesocúrtica
k>3 Lepticúrtica
k<3 Platicúrtica
Normal
Más agudas que la normal
Más planas que la normal