Este documento contiene la solución a dos ejercicios relacionados con grafos. En el primer ejercicio, se presenta un grafo no dirigido con 8 vértices y se piden varias operaciones como encontrar la matriz de adyacencia, comprobar si es conexo, regular o completo. En el segundo ejercicio, se da un digrafo con 6 vértices y también se piden operaciones como encontrar la matriz de conexión, comprobar si es simple y fuertemente conexo, y calcular distancias usando el algoritmo de Dijkstra.

1. UNIVERSIDAD FERMIN TORO
VICERRECTORADO ACADEMICO
FACULTA DE INGENIERIA
Andrés Palacios
23.903.545
Profesora Adriana Barreto
Cabudare, 6 de Junio del 2014

2. Solución al ejercicio 1
A) Matriz de adyacencia:
Ma=G
0 1 1 1 0 0 1 1
1 0 1 0 1 1 1 0
1 1 0 1 1 1 0 1
1 0 1 0 1 0 0 1
0 1 1 1 0 0 1 1
0 1 1 0 1 1 1 0
1 1 0 0 1 1 0 1
1 0 1 1 1 0 1 0

3. a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14 a15 a16 a17 a18 a19 a20
v1 1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
v2 1 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0
v3 0 1 1 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0
v4 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0
v5 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 1 0 1 0
v6 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 1
v7 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 1 1
v8 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 1 0 0
B) Matriz de incidencia:

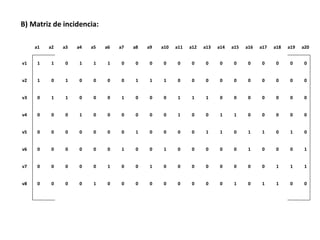
4. C) Es conexo? Justifique su respuesta.
R= Si es conexo ya que todos sus vértices están conectados entre si.
D) Es simple? Justifique su respuesta.
R= Si es simple porque el grafo no tiene lazos en ninguno de sus vértices y para cada
par de vértices distintos solo existe una arista.
E) Es regular? Justifique su respuesta.
R= No, porque todos sus vértices tienen el mismo grado.
F) Es completo? Justifique su respuesta.
R= No, porque no cumple con la definición de una arista por cada par de vértices.
G) Una cadena simple de grado 6.
C= [V1,a1,V2,a10,V6,a20,V7,a19,V5,a13,V3,a3,V2]
H) Un ciclo no simple de grado 5.
C= [V1,a2,V3,a12,V8,a15,V4,a4,V1,a2,V3]

5. I) Arbol generador aplicando el algoritmo constructor.
Seleccionar Vértice V1, H1 = {V1}
Arista 1 y H2= {V1,V2}
Arista 10 y H3= {V1,V2,V6}
Arista 20 y H4= {V1,V2,V6,V7}

6. Arista 19 y H5= {V1,V2,V6,V7,V5}
Arista 13 y H6= {V1,V2,V6,V7,V5,V3}
Arista 12 y H7= {V1,V2,V6,V7,V5,V3,V8}

7. Arista 15 y H8= {V1,V2,V6,V7,V5,V3,V8,V4}

8. J) Subgrafo parcial.

9. K) Demostrar si es euleriano aplicando el algoritmo de Fleury.
Seleccionamos a1 Seleccionamos a2
Seleccionamos a3 Seleccionamos a4

10. Seleccionamos a11 Seleccionamos a12
Seleccionamos a5 Seleccionamos a6

11. Seleccionamos a9 Seleccionamos a10
Seleccionamos a7 Seleccionamos a13

12. Seleccionamos a14 Seleccionamos a15
Seleccionamos a18 Seleccionamos a20

13. Seleccionamos a16
El grafo no es euleriano según el algoritmo de Fleury.
Se debe tomar en cuenta que un grafo es euleriano sólo si no tiene vértices de grado
impar y este no lo es ya que varios de sus vértices son de grado impar.

14. L) Demostrar si es hamiltoniano.
R= Existe un camino hamiltoniano ya que se puede pasar por cada vértice una vez sin
repetir ninguno.
Cadena hamiltoniano V1, V3, V2, V6, V7, V5, V8, V4
Existe también un ciclo hamiltoniano.
Ciclo hamiltoniano V1, V3, V2, V5, V6, V7, V8, V4, V1
Por lo tanto el grafo dado si es hamiltoniano.

15. Solución al ejercicio 2
A) Encontrar matriz de conexión
v1 v2 v3 v4 v5 v6
v1 0 1 1 0 1 0
v2 0 0 1 1 0 1
v3 0 0 0 1 1 0
v4 1 0 0 0 0 1
v5 0 1 0 1 0 1
v6 0 0 0 0 1 0
McD=

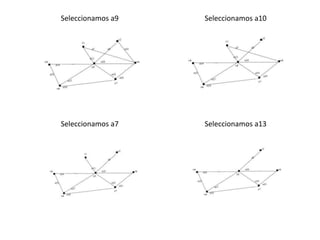
16. B) Es simple?. Justifique su respuesta
R= Si, porque no tiene lazos ni arcos paralelos.
C) Encontrar una cadena no simple no elemental de grado 5
T1=[V4,a12,V6,a14,V5,a10,V2,a4,V6,a14,V5]
D) Encontrar un ciclo simple
C1=[V1,a6,V5,a13,V6,a14,V5,a11,V4,a9,V1]

17. E) Demostrar si es fuertemente conexo utilizando la matriz de accesibilidad.
McD=
v1 v2 v3 v4 v5 v6
v1 0 1 1 0 1 0
v3 0 0 1 1 0 1
v3 0 0 0 1 1 0
v4 1 0 0 0 0 1
v5 0 1 0 1 0 1
v6 0 0 0 0 1 0

18. M2=
0 1 1 1 1 1
1 0 0 1 1 1
1 1 0 1 0 1
0 1 1 0 1 0
1 0 1 1 1 1
0 1 0 1 0 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
0 1 1 1 1 1
1 1 1 1 1 1
1 0 1 1 1 1
M3=
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
M4=
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
M5=

19. 1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
M6=
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
Mi=
Finalmente Acc(D)= bin=[I7 + M+M2+M3+M4+M5+M6]
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
31 40 33 65 62 79
22 33 24 47 47 58
20 26 22 39 43 49
16 29 21 42 38 48
23 34 25 49 53 60
11 14 12 23 23 30
=
Como la matriz de accesibilidad no tiene componentes nulos se puede afirmar que el
dígrafo es fuertemente conexo.

20. F) Encontrar la distancia de v2 a los demás vértices utilizando el algoritmo de Dijkstra
=[8,4](3)
=[7,3](2)
=[6,6](4) =[3,2](1)
=[0,-](0)
=[4,3](2)
=[4,2](1)

21. Ponderación de las aristas
Aristas a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14
Ponder. 2 3 4 3 2 3 4 1 4 3 2 2 4 3
D v2 a v1 = 8
D v2 a v3 = 3
D v2 a v4 = 4
D v2 a v5 = 6
D v2 a v6 = 3