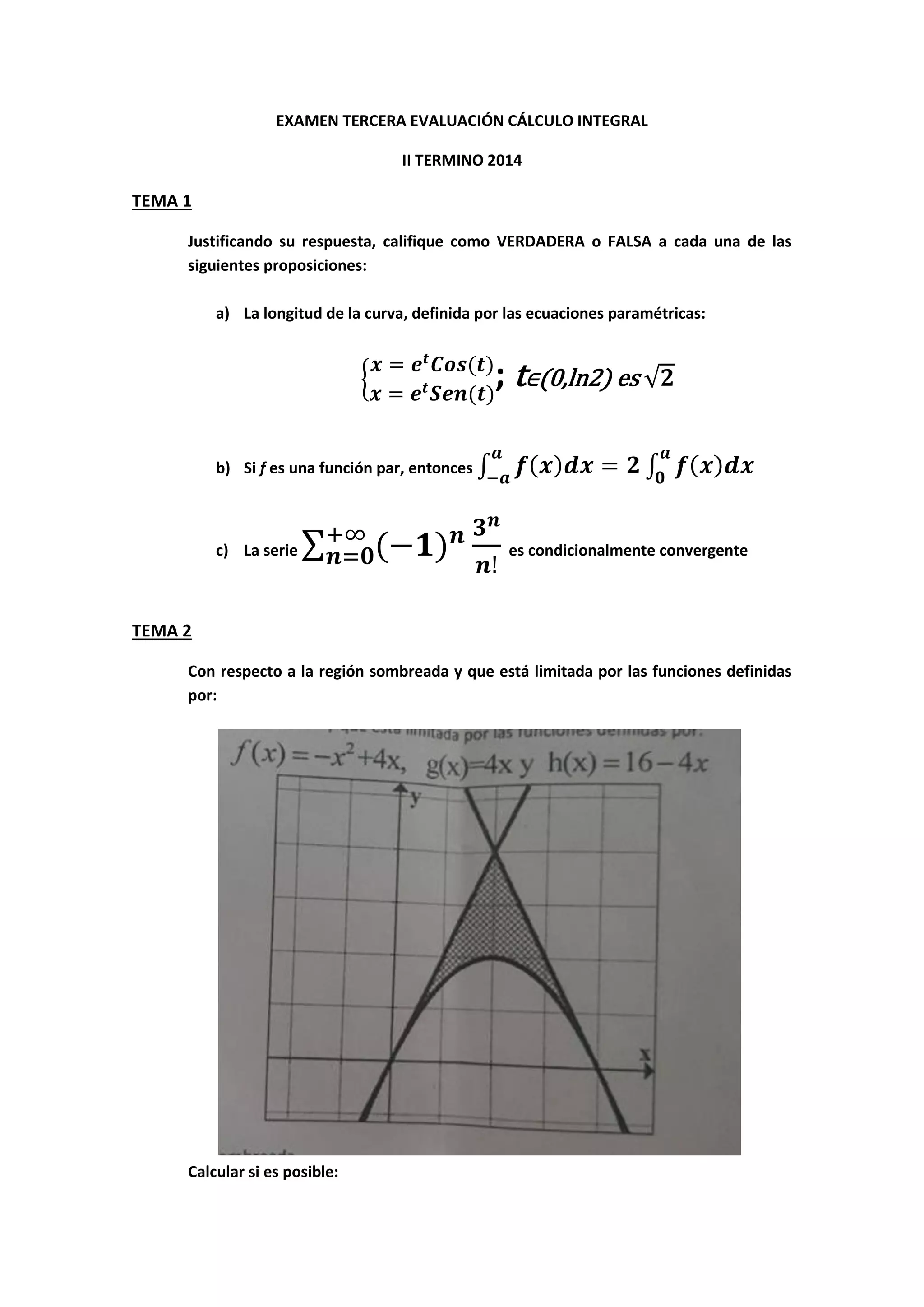
Este documento presenta 5 temas sobre cálculo integral para un examen. El Tema 1 contiene 3 proposiciones sobre longitud de curvas, integrales impares y convergencia condicional de series. El Tema 2 pide calcular el área y volumen de una región limitada por funciones. El Tema 3 contiene 4 antiderivadas. El Tema 4 solicita calcular el área de una región definida por una ecuación polar. El Tema 5 pide obtener la serie de Taylor y el intervalo de convergencia de la función f(x)=Cos(2x).

1. EXAMEN TERCERA EVALUACIÓN CÁLCULO INTEGRAL
II TERMINO 2014
TEMA 1
Justificando su respuesta, califique como VERDADERA o FALSA a cada una de las
siguientes proposiciones:
a) La longitud de la curva, definida por las ecuaciones paramétricas:
{ ; t∈(0,ln2) es √
b) Si f es una función par, entonces ∫ ∫
c) La serie ∑ es condicionalmente convergente
TEMA 2
Con respecto a la región sombreada y que está limitada por las funciones definidas
por:
Calcular si es posible:

2. a) El área de la región sombreada.
b) El volumen del sólido que se genera al rotar la región R alrededor de la recta
x=2
TEMA 3
Determinar las siguientes antiderivadas:
a) ∫
b) ∫
c) ∫
d) ∫
TEMA 4
a) Calcular el área de la región interior al rizo mayor y exterior al rizo menor del lugar
geométrico definido por la ecuación polar r=2-4Cos( )
TEMA 5
Dada la función f(x)=Cos(2x):
a) Obtenga su representación en serie de potencias de Taylor, alrededor de
b) Obtenga el intervalo de convergencia de la serie obtenida en el literal a)