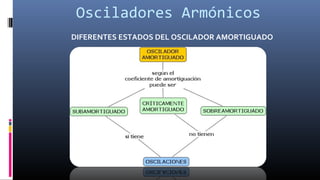
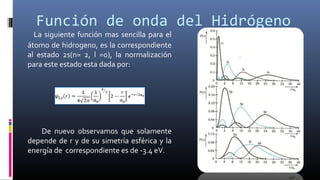
El documento aborda el desarrollo de la teoría cuántica, comenzando con las contribuciones de Max Planck y Albert Einstein en la comprensión de la radiación del cuerpo negro y el efecto fotoeléctrico. Se discuten las ideas de Niels Bohr sobre la estructura atómica y la dualidad onda-partícula propuesta por Louis de Broglie, junto con los fundamentos de la mecánica cuántica y ejemplos relevantes como el modelo del átomo de hidrógeno y el efecto Zeeman. Finalmente, se resaltan los distintos estados y propiedades de los osciladores armónicos en física.

2. INTRODUCCIÓN

3. Radiación de cuerpo negro
La “Catástrofe Ultravioleta”
Un cuerpo negro es un objeto teórico
o ideal que absorbe toda la luz y toda
la energía radiante que incide sobre él
sin reflejarla.
Fig.1 Experimento de cuerpo negro de Lummer y Kurlbaum.

4. La hipótesis de Max Planck
Trato de explicar el fenómeno de la
radiación del cuerpo negro dándose
cuenta que hacia falta considerar al
espectro electromagnético de forma
discreta (en cuantos de energía) y no
de manera continua como lo hace la
ecuación de Rayleigh-Jeans.
"La verdad nunca triunfa, simplemente sus oponentes se van muriendo.” – Max Planck
Max Karl Ernst Ludwig Planck (1858 – 1947)
Alemania.

5. Surgieron nuevas teorías
CUÁNTICAS
Basado en el trabajo de Planck, Einstein propuso
que la luz también entrega su energía en paquetes
(fotones).
Cada fotón con una energía equivalente a la
constante de Planck multiplicada por su frecuencia.
Desarrolló su teoría del efecto fotoeléctrico en 1905
y le valió el Premio Nobel de Física en 1921.
Albert Einstein (1879 –1955)
Inspirado por las ideas de Planck, aplicó con éxito
la idea de cuantización a la estructura del átomo.
Su modelo permitió explicar adecuadamente el
espectro del átomo de hidrógeno.
Introdujo el concepto de órbitas estacionarias,
Premio Nobel de Física en 1922 por su teoría de la
estructura atómica.
Niels Henrik David Bohr (1885 –1962)

6. De Broglie y la materia como
ondas
Se basó en la explicación del efecto fotoélectrico
de Einstein para pensar que si la luz presentaba un
comportamiento de partículas, entonces de igual
manera la materia se manifestaría como ondas.
De acuerdo con de Broglie es posible asociar a
cada partícula una longitud de onda cuántica dada
por la relación entre la constante de Planck y la
cantidad de movimiento.
Se confirmó su hipótesis tres años después para
los electrones con el experimento de doble ranura de
Young y recibió el Premio Nobel de Física en 1929.
Louis-Victor de Broglie (1892 –1987)
“Toda la materia presenta características tanto ondulatorias como corpusculares comportándose
de uno u otro modo dependiendo del experimento específico.”

7. El nacimiento formal de la
Mecánica Cuántica
Erwin Schrödinger (1887 –1961),
Su modelo atómico cuántico es el
actual.
Mecánica Cuántica, ¿basada en la probabilidad y de teoría no-determinista?
Werner Heisenberg (1901 –1976),
y el Principio de Incertidumbre.
Paul Dirac (1902 –1984),
y su ecuación de onda
relativista para el electrón.

8. Osciladores Armónicos
 Definición
 El oscilador armónico es uno de los sistemas más estudiados en la
física, ya que todo sistema que oscila alrededor de un punto de
equilibrio estable se puede estudiar en primera aproximación
como si fuera un oscilador
 Se dice que un sistema cualquiera, mecánico, eléctrico,
neumático, etc. es un oscilador armónico si cuando se deja en
libertad, fuera de su posición de equilibrio.

9. Osciladores Armónicos
 Característica
 La característica principal de un oscilador
armónico es que está sometido a una fuerza
recuperadora, que tiende a devolverlo al punto de
equilibrio estable, con una intensidad
proporcional a la separación respecto de dicho
punto

10. Osciladores Armónicos

11. Osciladores Armónicos
DIFERENTES ESTADOS DEL OSCILADOR AMORTIGUADO

12. Casos Relevantes
 Oscilador armónico Simple
 El oscilador armónico simple es el caso más sencillo, donde
únicamente se considera la fuerza recuperadora.
 Oscilador armónico amortiguado
 Este caso más realista consiste en tener en cuenta el
rozamiento del aire, que tiende a amortiguar la oscilación. El
modelo más usual consiste en tomar un rozamiento
proporcional a la velocidad.

13. Casos Relevantes
 Oscilador Simple reforzado
 Decimos que un oscilador está forzado si sobre él se aplica una
fuerza externa. El caso más interesante es cuando la fuerza de
forzamiento es también periódica, por ejemplo sinusoidal.
 Oscilador Simple resonante
 Las amplitudes del desplazamiento y de la velocidad para la
solución estacionaria del oscilador amortiguado dependen de
las características físicas del oscilador y de la frecuencia de la
fuerza aplicada.

14. Casos Relevantes
 Oscilador amortiguado y forzado
 El oscilador amortiguado forzado considera una
fuerza externa oscilante que se ejerce sobre el
sistema de la forma:

15. El átomo de Hidrógeno
 Se visualiza el electrón como una partícula
que orbita alrededor del núcleo en niveles
cuantiados no radiantes de energía, según
el modelo atómico de Bohr.
 Pero De Broglie otorgo a los electrones
una naturaleza ondulatoria.

16. El átomo de Hidrógeno
 La ecuación para la energía
potencial del átomo de hidrogeno
es:
 Donde ‘k’ e s la constante de
coulomb, y r es la distancia radial
desde el protón (situado en r = 0)
hasta el electrón.
 De acuerdo con la mecánica
cuántica las energías para los
estados permitidos para el átomo de
hidrogeno están dadas por:
Se puede reemplazar los n por n=1,2,3,…

17. El átomo de Hidrógeno
 Esto concuerda con la teoría de Bohr donde
la energía depende solo de los números
cuánticos n.
 En los problemas unidimensionales solo se
necesita un número cuántico n, pero en los
problemas tridimensionales del átomo de
hidrogeno se requiere tres números
cuánticos por cada estado estacionario y
son:
o n: número cuántico principal
o l: número cuántico orbital
o ml: número cuántico orbital magnético.
o Las restricciones para estos números son:
o n: pueden variar desde 1 hasta ∞
o l: pueden variar desde 0 hasta n-1
o ml: pueden variar desde –l hasta l.

18. Función de onda del Hidrógeno
Ya que la energía potencial del hidrogeno
depende de la distancia radial r, se podría
esperar que algunos de los estados permitidos
puedan ser representados por la función de
onda que dependa solo de r,
 La función de onda más simple que describe el
estado 1s y se designa como:
 Donde a es el radio de Bohr dado por dado por :
Donde
 es la constante de Planck.
 m la masa del electrón en vacío.
 k es la constante de coulomb.

19. Función de onda del Hidrógeno
La ecuación de onda es simétricamente esférica.
 De hecho es verdad para todo el estado s, y por otro lado ψ depende de otras
variables páralos estados l mayor de cero.
 Recordando la densidad de probabilidad (esto es, la probabilidad por unidad de
volumen) de hallar un electrón en cualquier punto es igual a |ψ|^2, y la ecuación
es:
Es conveniente definir la función densidad de probabilidad radial P(r) como la
probabilidad de hallar un electrón en una concha esférica de radio r y espesor dr
Se obtiene:
Y sustituyendo la ecuación en la ecuación anterior queda:

20. Función de onda del Hidrógeno
La siguiente función mas sencilla para el
átomo de hidrogeno, es la correspondiente
al estado 2s(n= 2, l =0), la normalización
para este estado esta dada por:
De nuevo observamos que solamente
depende de r y de su simetría esférica y la
energía de correspondiente es de -3.4 eV.

21. Ejemplo 1:
Ejemplo 2:

22. El efecto Zeeman
 El efecto Zeeman es el desdoblamiento
de los rayos espectrales debido a la
presencia de un fuerte campo
magnético, en el efecto Zeeman un
campo magnético actúa sobre la
emisión de la luz por parte de un átomo,
éste en ausencia de todo campo
magnético, emite determinados colores
o frecuencias, irradia un espectro más
complicado al colocarlo en un campo
magnético. Pieter Zeeman (1865 – 1943)

23. El efecto Zeeman
 Cuando se coloca un átomo en un campo magnético se
observa un desdoblamiento de las líneas espectrales este
efecto fue observado por primera vez por Zeeman.
Podemos calcular clásicamente el valor de la variación de
la frecuencia; debida a la acción del campo magnético
sobre una carga oscilante, la cual resulta en:
 e, m – carga y masa del oscilador
 B intensidad del campo externo.
Resulta un desdoblamiento en las líneas espectrales con
una línea central sin conimiento, esto se denomina efecto
Zeeman normal, mientras que en algunos casos el
desdoblamiento es mayor que los componentes con
separaciones que no corresponden al clásico y se
denomina efecto Zeeman anomalo.
Pieter Zeeman (1865 – 1943)

24. El efecto Zeeman
 El efecto Zeeman normal aparece sólo en
transiciones entre estados atómicos con Spin
total S = 0.
 El impulso angular total de un
estado es entonces un impulso angular
orbital puro (J=L)
 Ahora si calculamos el Hamiltoniano se
tendría que: Pieter Zeeman (1865 – 1943)

25. FIN

27. “Einstein, deje de decirle a Dios lo que debe
hacer con sus dados.” –Bohr.
“Dios no juega a los dados.”
–Einstein.

28. Física Moderna – Lic. Benjamín Albor S.
Presentado Por:
Díaz Danilso
Juliao Alberto
Quintero Laureano
Ramírez Jhony
Universidad Autónoma del Caribe
2012