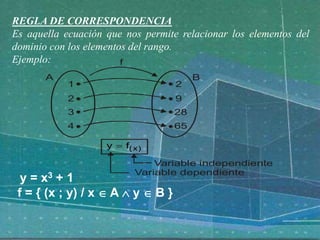
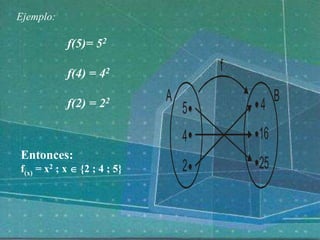
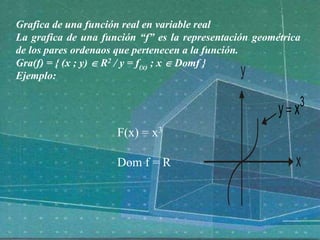
Este documento describe las funciones reales de variable real, incluyendo su dominio y rango, la regla de correspondencia que relaciona elementos del dominio con el rango, y cómo graficar una función real. Proporciona ejemplos de funciones como f(x)=x2 y f(x)=x3 para ilustrar estas ideas.

2. FUNCIÓN REAL DE VARIABLE REAL
Son aquellas funciones cuyo dominio y rango es
un subconjunto de R.
Ejemplo:
f = 0 ,1)  R
f : R  R
DOMINIO:
Dom(f) = { x / (x ; y)  f }
RANGO:
Ran(f) = { y / (x ; y)  f }

3. REGLA DE CORRESPONDENCIA
Es aquella ecuación que nos permite relacionar los elementos del
dominio con los elementos del rango.
Ejemplo:
1
2
3
4
A B
f
2
9
28
65
)x(fy 
Variable independiente
Variable dependiente
y = x3 + 1
f = { (x ; y) / x  A  y  B }

4. Ejemplo:
f(5)= 52
f(4) = 42
f(2) = 22
2
5
4
A B
f
16
25
4
Entonces:
f(x) = x2 ; x  {2 ; 4 ; 5}

5. Grafica de una función real en variable real
La grafica de una función “f” es la representación geométrica
de los pares ordenaos que pertenecen a la función.
Gra(f) = { (x ; y)  R2 / y = f(x) ; x  Domf }
Ejemplo:
x
y
3
xy 
F(x) = x3
Dom f = R