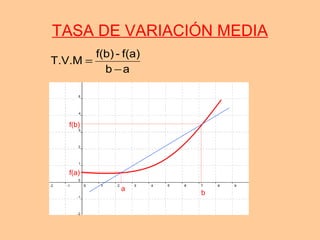
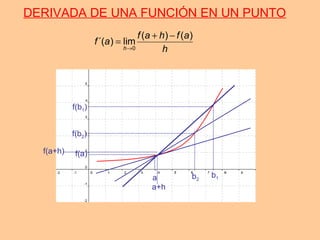
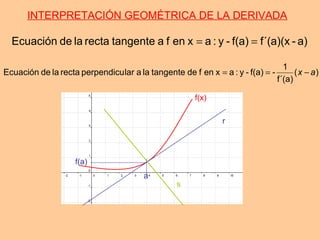
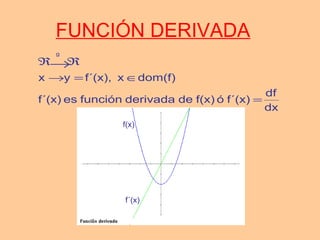
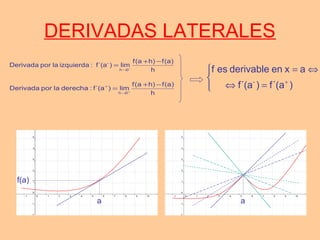
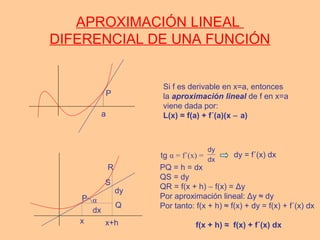
Este documento resume conceptos clave sobre derivadas de funciones, incluyendo la derivada de una función en un punto y su interpretación geométrica, las derivadas de operaciones con funciones como suma, producto y composición, la derivación logarítmica, y la aproximación lineal utilizando la diferencial de una función.

1. Unidad 10 DERIVADAS
• Derivada de una función en un punto.
Interpretación geométrica.
• Función derivada. Continuidad y derivabilidad.
• Derivada de las operaciones con funciones.
• Derivada de la función compuesta e inversa.
• Derivada de funciones. Tabla de derivadas.
• Derivación logarítmica.
• Diferencial de una función

2. TASA DE VARIACIÓN MEDIA
a
b
f(a)
f(b)
ab
f(a)-f(b)
T.V.M
−
=

3. a b1b2
f(a)
f(b2)
f(b1)
a+h
f(a+h)
DERIVADA DE UNA FUNCIÓN EN UN PUNTO
h
afhaf
af
h
)()(
lim)´(
0
−+
=
→

4. INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA
a)-f´(a)(xf(a)-y:axenfatangenterectaladeEcuación ==
)(
f´(a)
1
-f(a)-y:axenfdetangentelaalarperpendicurectaladeEcuación ax −==
f(x)
r
s
a
f(a)

5. FUNCIÓN DERIVADA
dx
df
f´(x)óf(x)dederivadafunciónesf´(x)
dom(f)xf´(x),yx
g
=
∈=→
ℜℜ→
f´(x)
f(x)

6. DERIVADAS LATERALES
h
)a(f)ha(f
lim)f´(a:izquierdalaporDerivada
0h
- −+
= −
→
h
)a(f)ha(f
lim)f´(a:derechalaporDerivada
0h
−+
= +
→
+



=⇔
⇔=
+
)a´(f)f´(a
axenderivableesf
-
a
f(a)
a

7. DERIVADA DE LAS OPERACIONES CON FUNCIONES
Sean f, g funciones derivables en x = a, k ε ℝ.
(k · f)´(a) = k · f´(a)
(f + g)´(a) = f´(a) + g´(a)
(f · g)´(a) = f´(a) · g(a) + f(a) · g´(a)
(f ◦ g)´(a) = f´(g(a)) · g´(a) (Regla de la cadena)
)a(g
)a´(g)a(f)a(g)a´(f
)a(
g
f
2
⋅−⋅
=
′






( ) ( ))(´
1
)´( 1
1
xff
xf −
−
=

8. TABLA DE DERIVADAS
y'=1y=xy'=1y=x
y'=0y=8y'=0y=k

9. DERIVACIÓN LOGARÍTMICA
La derivación logarítmica es una estrategia que nos permite calcular
con facilidad las derivadas de funciones exponenciales.
Ejemplo:
( )
( )( ) ( )
( )
( )
( ) ( ) 





+
⋅++⋅⋅+=






+
⋅++⋅⋅=
+
⋅++⋅=
+⋅=+=
+=
1x
x2
xsen1xlnxcos1xf´(x):tantoPor
1x
x2
xsen1xlnxcosf(x)f´(x)Despejando
1x
x2
xsen1xlnxcos
)x(f
)x´(f
:Derivamos
1xlnxsen1xlnf(x)ln:logaritmosTomamos
1x)x(f
2
2xsen2
2
2
2
2
2xsen2
xsen2

10. APROXIMACIÓN LINEAL
DIFERENCIAL DE UNA FUNCIÓN
P
a
Si f es derivable en x=a, entonces
la aproximación lineal de f en x=a
viene dada por:
L(x) = f(a) + f´(a)(x − a)
P
x x+h
dx
Q
R
S
dy
α
tg α = f´(x) = dx
dy
dy = f´(x) dx
PQ = h = dx
QS = dy
QR = f(x + h) − f(x) = Δy
Por aproximación lineal: Δy ≈ dy
Por tanto: f(x + h) ≈ f(x) + dy = f(x) + f´(x) dx
f(x + h) ≈ f(x) + f´(x) dx