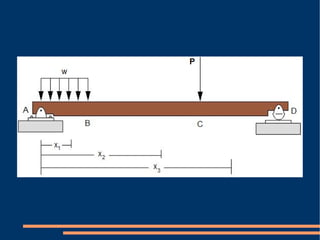
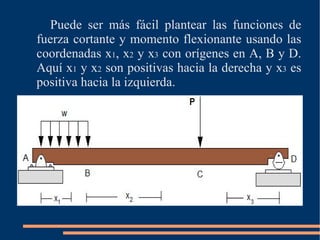
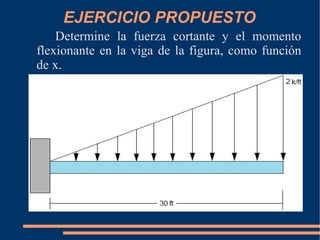
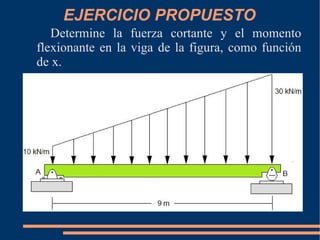
Este documento describe cómo calcular las funciones de fuerza cortante y momento flexionante a lo largo de una viga. Explica que estas funciones deben determinarse por secciones separadas entre discontinuidades de carga. Proporciona un procedimiento para determinar V y M como funciones de la posición x mediante el análisis de fuerzas y momentos en diagramas de cuerpo libre de secciones cortadas. Finalmente, presenta un ejercicio propuesto para aplicar este método a una viga específica.

1. UNIVERSIDAD DE ACONCAGUA SEDE TEMUCO FUNCIONES DE FUERZA CORTANTE Y MOMENTO FLEXIONANTE Asignatura: Estructuras II Profesor: Paolo Castillo

2. Las vigas son miembros estructurales diseñados para soportar cargas laterales, esto es, cargas aplicadas perpendicularmente a sus ejes. El diseño de tales miembros requiere un conocimiento detallado de las variaciones de la fuerza cortante interna V y del momento flexionante M que actúan en cada punto a lo largo del eje de la viga. INTRODUCCIÓN

3. La fuerza normal interna, generalmente no se considera por: En la mayoría de los casos, las cargas aplicadas a una viga actúan perpendicularmente al eje de la viga y producen, por tanto, sólo una fuerza cortante interna y un momento flexionante. Para fines de diseño la resistencia de la viga a la fuerza cortante y particularmente a la flexión, es más importante que su capacidad para resistir fuerza normal. Sin embargo, una importante excepción a esto se presenta cuando las vigas están sometidas a fuerzas axiales de compresión, ya que el pandeo o inestabilidad que puede ocurrir tiene que investigarse.

4. Funciones de V y M Las variaciones de V y M, como función de la posición x de un punto arbitrario a lo largo del eje de una viga, pueden obtenerse usando el método de las secciones, analizado anteriormente. Sin embargo, aquí es necesario localizar la sección imaginaria o corte a una distancia x arbitraria desde un extremo de la viga y no en un punto específico. En general, las funciones internas de fuerza cortante y momento flexionante serán discontinuas, o sus pendientes serán discontinuas, en puntos en el que el tipo o magnitud de la carga distribuida cambia o ahí donde fuerzas o momentos concentrados se aplican.

5. Debido a lo anterior, las funciones de fuerza cortante y momento flexionante deben determinarse para cada región de la viga localizada entre dos discontinuidades cualesquiera de carga. Por ejemplo, tendrían que usarse las cordenadas x 1 , x 2 y x 3 para describir la variación de V y M en toda la longitud de la viga de la figura siguiente. Esas coordenadas serán válidas sólo dentro de la región de A y B para x 1 , de B y C para x 2 y de C y D para x 3 . Aunque cada una de esas coordenadas tiene el mismo origen, como es el caso aquí, no necesariamente tiene que ser siempre así.

7. Puede ser más fácil plantear las funciones de fuerza cortante y momento flexionante usando las coordenadas x 1 , x 2 y x 3 con orígenes en A, B y D. Aquí x 1 y x 2 son positivas hacia la derecha y x 3 es positiva hacia la izquierda.

8. PROCEDIMIENTO DE ANÁLISIS El siguiente procedimiento proporciona un método para determinar las variaciones de la fuerza cortante y el momento flexionante en una viga en función de la posición x. REACCIONES EN LOS SOPORTES. Determinar las reacciones de los soportes sobre la viga y resolver todas las fuerzas externas en componentes que actúan paralela y perpendicularmente al eje de la viga.

9. FUNCIONES FUERZA CORTANTE Y MOMENTO FLEXIONANTE. Especificar coordenadas x separadas y orígenes asociados que se extiendan hacia las regiones de la viga entre fuerzas y/o momentos concentrados o donde se tenga una discontinuidad de la carga distribuida. Seccionar la viga perpendicularmente a su eje en cada distancia x y del diagrama de cuerpo libre de uno de los segmentos determine las incógnitas V y M en la sección cortada como funciones de x. Sobre el diagrama de cuerpo libre, V y M deben mostrarse actuando en sus direcciones positivas. V se obtiene con la sumatoria de fuerzas en Y; M se obtiene con la sumatoria de momentos respecto a un punto S localizado en la sección cortada

10. EJERCICIO PROPUESTO Determine la fuerza cortante y el momento flexionante en la viga de la figura, como función de x.

11. EJERCICIO PROPUESTO Determine la fuerza cortante y el momento flexionante en la viga de la figura, como función de x.