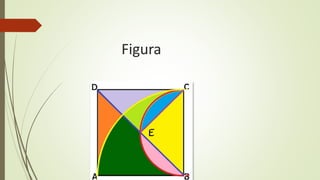
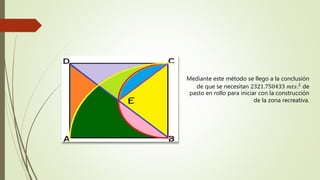
El documento presenta fórmulas matemáticas para calcular el área de diferentes secciones de una figura geométrica. Se proporcionan las fórmulas para calcular el área de un sector circular, triángulo, semicírculo y segmento circular. Luego, aplica estas fórmulas a una figura específica para calcular cada área y determinar el área total requerida de pasto para construir la zona recreativa.

1. Problema Matemático
Mises Castañeda García
2 C
Procesos Industriales

2. Fórmulas a utilizar en el procedimiento para las
áreas sombreadas para la siguente figura
 𝐴𝑠𝑔 =
𝐴𝑐𝑠−𝐴𝑡
2
= Área de segmento circular(fondo azul)
 𝐴𝑐𝑐 =
𝜋𝑟2
4
𝑜
𝜋𝑟2∝
360
= Área de un sector circular(línea amarilla).
 𝐴𝑣 =
𝐴𝑡𝑐
2
− 𝐴𝑒 − 𝐴𝑖𝑟 = Área sombreada color verde.
 𝐴𝑒 =
𝐴𝑡𝑐−𝐴𝑐𝑐
2
= Área de embecadura(fondo morado)
 𝐴𝑠𝑐 =
𝜋𝑟2∝
360
=Área del semicírculo(línea roja)
 𝐴𝑖𝑟 =
𝐴𝑡
2
− 𝐴𝑡 − 𝐴𝑠𝑔 − 𝐴𝑖𝑟 = Área irregular
 𝐴𝑡 =
𝑏∗ℎ
2
=- Área de un Triángulo(fondo amarillo).

3. Figura

4.  Obtener el valor de uno de sus lados
𝐿 = 𝐴 = 7225 = 85 𝑚𝑡𝑠.2
 Obtener el área del sector circular
𝐴𝑐𝑐 =
𝜋𝑟2
4
=
𝜋(85)2
4
=
22698.00692
4
= 5674.501731 𝑚𝑡𝑠.2
 Obtener área del triángulo
𝐴𝑡 =
𝑏 ∗ ℎ
2
=
85 ∗ 42.5
2
= 1806.25 𝑚𝑡𝑠.2
 Obtener el área del semicírculo.
𝐴𝑠𝑐 =
𝜋𝑟2
∝
360
=
𝜋 42.5 2
180
360
= 2837.250865 𝑚𝑡𝑠.2
 Obtener el área del segmento circular
𝐴𝑠𝑔 =
𝐴𝑐𝑠 − 𝐴𝑡
2
=
2837.250865 −1806.25
2
=
1031.000865
2
= 515.5004326 𝑚𝑡𝑠.2

5. Mediante este método se llego a la conclusión
de que se necesitan 2321.750433 𝑚𝑡𝑠.2 de
pasto en rollo para iniciar con la construcción
de la zona recreativa.