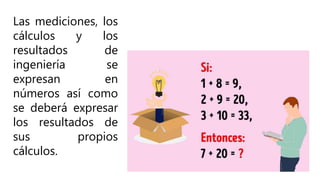
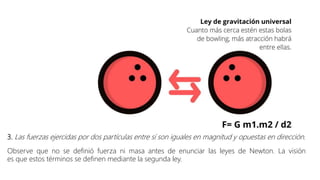
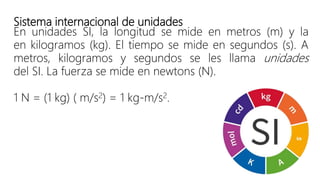
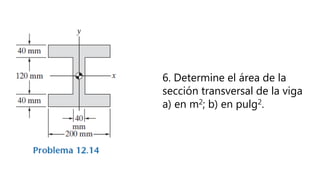
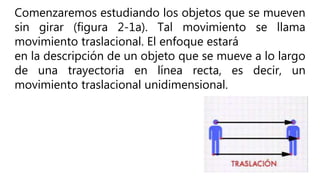
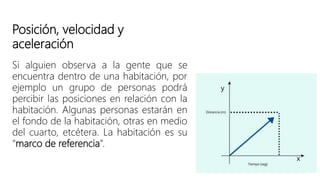
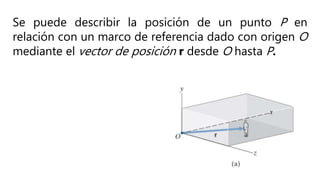
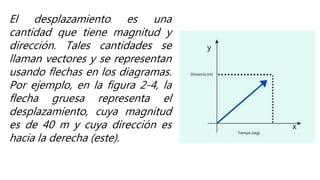
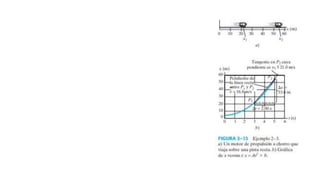
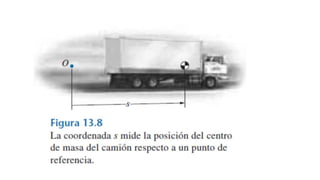
Este documento presenta una introducción a la mecánica elemental. Se divide la mecánica elemental en estática, que es el estudio de objetos en equilibrio, y dinámica, que es el estudio de objetos en movimiento. También describe conceptos fundamentales como posición, velocidad, aceleración, fuerzas y leyes de Newton. Finalmente, presenta algunos problemas de mecánica elemental para resolver.

1. Introducción a la Fisica
Presenta: Dr. Ing. Ángel
Francisco Villalpando
Reyna

2. La Mecánica Elemental se divide
en Estática, que es el estudio de los
objetos en equilibrio, y Dinámica,
que es el estudio de los objetos en
movimiento. Los resultados
obtenidos en la mecánica elemental
se aplican directamente a muchos
campos de la ingeniería.

3. La Mecánica fue la primera ciencia analítica, por eso los conceptos fundamentales, los métodos analíticos y las
analogías de la mecánica se encuentran en casi todas las ramas de la ingeniería.

4. Resolución de problemas

5. Aunque los
diferentes
tipos de
problemas
requieren
distintos
métodos, los
siguientes
pasos se
aplican a
muchos de
ellos:

6. • Identifique la información
dada y la información, o
respuesta, que debe
determinarse. Con frecuencia
resulta útil reformular el problema
en sus propias palabras. Cuando
sea apropiado, asegúrese de que
entiende el sistema físico o el
modelo involucrado.

7. • Desarrolle una estrategia para el problema.
Cuando sea posible, dibuje diagramas para visualizar y resolver el
problema.

8. • Siempre que pueda, trate de predecir la respuesta. Esto desarrollará
su intuición y lo ayudará a reconocer una respuesta incorrecta.

9. • Resuelva las
ecuaciones y, cuando
sea posible, interprete
sus resultados y
compárelos con su
predicción. El último
paso se llama
verificación en la
realidad. ¿Es razonable
su respuesta?

10. Números

11. Las mediciones, los
cálculos y los
resultados de
ingeniería se
expresan en
números así como
se deberá expresar
los resultados de
sus propios
cálculos.

13. Dígitos significativos Este
término se refiere al
número de dígitos
significativos (o sea,
exactos) en un número,
contando hacia la
derecha a partir del
primer dígito distinto de
cero.

14. Los números 7.630 y 0.007630 están expresados con
cuatro dígitos significativos. Si se sabe que sólo los
primeros cuatro dígitos del número 7,630,000 son
exactos, esto se puede indicar escribiendo el número
en notación científica como 7.630 x 106.

15. Los números pueden redondearse a cierta cantidad de
dígitos significativos.
Por ejemplo, el valor de puede expresarse con tres
dígitos significativos, 3.14, o con seis dígitos
significativos, 3.14159.

16. Espacio y tiempo
El espacio se refiere simplemente al
universo tridimensional en que vivimos.
Las experiencias diarias proporcionan
una noción intuitiva del espacio y las
ubicaciones, o posiciones, de los
en éste. La distancia entre dos puntos
en el espacio es la longitud de la línea
recta que los une.

17. La generalización de este procedimiento para la
adición de tres o más vectores es clara y conduce a la
propiedad de asociatividad de la adición (ver figura
1.4), por ejemplo

18. Si la posición de un punto en el espacio en relación
con algún punto de referencia cambia con el tiempo,
La razón del cambio de su posición se llama
velocidad (m/s) , y la razón del cambio de su
velocidad se denomina aceleración (m/s2).

19. Leyes de Newton
La mecánica elemental se estableció sobre
una base sólida con la publicación en 1687
de Philosophiae Naturalis Principia
Mathematica de Isaac Newton.
Newton enunció tres “leyes” del
movimiento que, expresadas en términos
modernos, son:

20. 1. Cuando la suma de las fuerzas que actúan sobre
una partícula es igual a cero, su velocidad es
constante. En particular, si inicialmente la partícula se
encuentra en reposo, permanecerá en reposo.

21. 2. Cuando la suma de las fuerzas que actúan sobre una partícula no es igual a
cero, la suma de las fuerzas es igual a la razón de cambio de la cantidad de
movimiento lineal de la partícula.
Si la masa es constante, la suma de las fuerzas es igual al producto de la masa
la partícula y su aceleración.

22. 3. Las fuerzas ejercidas por dos partículas entre sí son iguales en magnitud y opuestas en dirección.
Observe que no se definió fuerza ni masa antes de enunciar las leyes de Newton. La visión
es que estos términos se definen mediante la segunda ley.

23. Sistema internacional de unidades
En unidades SI, la longitud se mide en metros (m) y la
en kilogramos (kg). El tiempo se mide en segundos (s). A
metros, kilogramos y segundos se les llama unidades
del SI. La fuerza se mide en newtons (N).
1 N = (1 kg) ( m/s2) = 1 kg-m/s2.

24. Unidades de uso común en el sistema Ingles
En las unidades de uso común en Estados Unidos, la longitud se
en pies y la fuerza en libras (lb). El tiempo se mide en segundos (s).
Éstas son las unidades básicas. En este sistema de unidades la masa
una unidad derivada.
Slug es una unidad de masa en el Sistema Pie-Libra-Segundo)
1 lbf = 1 𝑠𝑙𝑢𝑔 1
𝑝𝑖𝑒
𝑠2
A partir de esta expresión se obtiene
1 𝑠𝑙𝑢𝑔 = 1
𝑙𝑏∙𝑠2
𝑝𝑖𝑒

25. Unidades angulares
En ambos sistemas de unidades los
ángulos se expresan normalmente en
radianes (rad). En la figura 12.2 se
muestra el valor de un ángulo u en
radianes. Se define como la razón de la
parte de la circunferencia subtendida
θ y el radio del círculo.
2𝜋𝑅 = 360°

26. Conversión de unidades
En la práctica de la ingeniería
muchas situaciones que requieren
convertir valores expresados en
unidades de una clase a valores en
otras unidades. La conversión de
unidades es directa pero debe
hacerse con cuidado.

27. Problemas

28. 1. Un hombre maneja una bicicleta a una velocidad de 6
metros por segundo (m/s). ¿Qué tan rápido se desplaza en
kilómetros por hora (km/h)?

29. 2. La presión ejercida en un punto del casco del vehículo de
sumersión profunda es de 3.00 x 106 Pa (pascales). Un pascal
es 1 newton por metro cuadrado. Determine la presión en
libras por pie cuadrado y una libra por pulgada cuadrada.

30. 3. El Burj Dubai, que debe estar
terminado en 2008, será el edificio
más alto del mundo, con una altura
de 705 m. El área de su base será de
8000 m2. Convierta su altura y su área
de base a unidades de uso común en
Estados Unidos con tres dígitos
significativos.

31. 4. Suponga que acaba de comprar un Ferrari F355 coupe y desea saber si puede
usar su juego de llaves SAE (unidades de uso común en Estados Unidos) para
trabajar en él. Usted tiene llaves con anchos w = 1/4 pulg, 1/2 pulg, 3/4 pulg y 1
pulg y el automóvil tiene tuercas con dimensiones n = 5 mm, 10 mm, 15 mm, 20
mm y 25 mm. Si se establece que una llave ajusta si w no es 2% mayor que n, ¿cuál
de sus llaves puede usar?

32. 5. La aceleración debida a la gravedad al nivel del mar en unidades SI
es g = 9.81 m/s2. Mediante la conversión de unidades, utilice este
valor para determinar la aceleración debida a la gravedad al nivel del
mar en unidades de uso común en Estados Unidos.

33. 6. Determine el área de la
sección transversal de la viga
a) en m2; b) en pulg2.

34. 7. Las cargas
distribuidas sobre
vigas se expresan en
unidades de fuerza por
unidad de longitud. Si
el valor de una carga
distribuida es de 400
N/m, ¿cuál es su valor
en lb/pie?

35. 8. El momento de inercia del área rectangular con respecto al eje x está dado por la
ecuación
𝐼 =
1
3
𝑏ℎ3
Las dimensiones del área son b 200 mm y h 100 mm. Determine el valor de I con
cuatro dígitos significativos en términos de a) mm4, b) m4, y c) pulg4

36. 9. Un transductor de
presión mide un valor
de 300 lb/pulg2.
Determine el valor de
la presión en pascales.
Un pascal (Pa) es igual
a un newton por metro
cuadrado.

37. 10. Un caballo de fuerza equivale a 550 pies-lb/s. Un watt es
igual a 1 N-m/s. Determine cuántos watts son generados
por los motores de un jet comercial, si éstos producen 7000
caballos de fuerza.

38. Movimiento de un Punto
En este capítulo se inicia el estudio del movimiento.
Aquí no se tiene interés en las propiedades de los
objetos ni en las causas de sus movimientos; el
objetivo consiste sólo en describir y analizar el
movimiento de un punto en el espacio.

39. MOVIMIENTO DE UN PUNTO

40. Comenzaremos estudiando los objetos que se mueven
sin girar (figura 2-1a). Tal movimiento se llama
movimiento traslacional. El enfoque estará
en la descripción de un objeto que se mueve a lo largo
de una trayectoria en línea recta, es decir, un
movimiento traslacional unidimensional.

41. Posición, velocidad y
aceleración
Si alguien observa a la gente que se
encuentra dentro de una habitación, por
ejemplo un grupo de personas podrá
percibir las posiciones en relación con la
habitación. Algunas personas estarán en
el fondo de la habitación, otras en medio
del cuarto, etcétera. La habitación es su
“marco de referencia”.

42. Un marco de referencia
es simplemente un
sistema coordenado que
es adecuado para
especificar posiciones de
puntos.

43. POSICION
En física con frecuencia se dibuja un sistema de ejes
coordenados, como se muestra en la figura 2-3,
representar un marco
de referencia. Siempre podemos elegir la posición
del origen (0) y el sentido de los ejes x y y como
mejor nos convenga. Los ejes x y y siempre son
perpendiculares entre sí.
Los objetos situados a la derecha del origen de
coordenadas (0) sobre el eje x tienen una
coordenada x que usualmente se considera
del mismo modo, los puntos situados a la izquierda
del 0 usualmente tienen una coordenada x negativa

44. Se puede describir la posición de un punto P en
relación con un marco de referencia dado con origen O
mediante el vector de posición r desde O hasta P.

45. Es necesario hacer una distinción entre la distancia
recorrida por un objeto y su desplazamiento, el cual se
define como el cambio de posición del objeto. Es decir,
el desplazamiento muestra qué tan lejos está el objeto
del punto de partida.

46. El desplazamiento es una
cantidad que tiene magnitud y
dirección. Tales cantidades se
llaman vectores y se representan
usando flechas en los diagramas.
Por ejemplo, en la figura 2-4, la
flecha gruesa representa el
desplazamiento, cuya magnitud
es de 40 m y cuya dirección es
hacia la derecha (este).

47. Velocidad promedio
El aspecto más evidente del movimiento de un objeto es
tan rápido se mueve, es decir, su rapidez o velocidad.
El término “rapidez” se refiere a qué tan lejos viaja un
en un intervalo de tiempo dado, independientemente de la
dirección y el sentido del movimiento.

48. Los términos “velocidad” y “rapidez” a menudo se utilizan
indistintamente en el lenguaje cotidiano. Sin embargo, en física
hacemos una distinción entre ambos. La rapidez es simplemente un
número positivo con unidades. Por otro lado, el término velocidad se
usa para indicar tanto la magnitud (es decir, el valor numérico) de qué
tan rápido se mueve un objeto, como la dirección en la que se mueve.
(Por lo tanto, la velocidad es un vector). Existe una segunda diferencia
entre rapidez y velocidad; a saber, la velocidad promedio.

50. Velocidad promedio de un corredor. La posición de un
corredor en función del tiempo se grafica conforme se
mueve a lo largo del eje x de un sistema coordenado.
Durante un intervalo de tiempo de 3.00 s, la posición del
corredor cambia de x1 = 50.0 m a x2 = 30.5 m, como se
muestra en la figura 2-7. ¿Cuál fue la
velocidad promedio del corredor?

51. Distancia recorrida por un ciclista. ¿Qué distancia puede
recorrer un ciclista en 2.5 h a lo largo de un camino recto, si
su velocidad promedio es de 18 km/h?

52. Velocidad instantánea
Si usted conduce un automóvil a lo largo de un camino recto de 150 km en 2.0 h,
magnitud de su velocidad promedio es de 75 km/h. Sin embargo, es improbable
que se haya desplazado precisamente a 75 km/h en cada instante. Para describir
esta situación, necesitamos el concepto de velocidad instantánea, que es la
velocidad en cualquier instante de tiempo. (Su magnitud es el número, con
unidades, que indica un velocímetro, como el de la figura 2-8). Con más
la velocidad instantánea en cualquier momento se define como la velocidad
promedio durante un intervalo de tiempo infinitesimalmente

53. Problema
Dada x como función de t. Un motor de propulsión a chorro se
lo largo de una pista experimental (que llamamos el eje x) como se
muestra en la figura 2-13a. Trataremos al motor como si fuera una
partícula. Su posición en función del tiempo está dada por la ecuación
= At2 + B, donde A = 2.10 m/s2 y B =
2.80 m; esta ecuación se grafica en la figura 2-13b. a) Determine el
desplazamiento del motor durante el intervalo de tiempo de t1 = 3.00
a t2 = 5.00 s. b) Determine la velocidad promedio durante este
de tiempo. c) Determine la magnitud de
la velocidad instantánea en t = 5.00 s

55. Movimiento en línea recta
Este tipo simple de movimiento se analiza para
evaluar situaciones prácticas los ingenieros deben
analizar movimientos en línea recta, como el
movimiento de un vehículo sobre un camino recto o
el movimiento de un pistón en un motor de
combustión interna.

56. Descripción del movimiento
Considere una línea recta que pasa por el origen O
un marco de referencia dado.
Se puede especificar la posición de un punto P sobre
una línea recta respecto a O por medio de una
coordenada s medida a lo largo de la línea que va de
a P.

58. Análisis del movimiento
En algunas situaciones se conoce la posición s de algún
objeto como función del tiempo. Los ingenieros usan
métodos como el radar y la interferometría de láser para
medir posiciones en función del tiempo. En este caso, con
las ecuaciones (13.3) y (13.4) pueden obtenerse por
diferenciación la velocidad y la aceleración como
del tiempo.

60. Problemas

61. 4. La fresadora que se muestra en la figura está programada de modo que
durante el intervalo de tiempo desde t = 0 hasta t = 2s, la posición de su cabeza
(en pulgadas) está dada como una función del tiempo por s = 4t - 2t2. ¿Cuál es la
velocidad (en pulg/s) y la aceleración (en pulg/s2) de la cabeza cuando t = 1s?

62. 5. La posición del bote que se muestra en la figura durante el intervalo de tiempo
desde t = 2s hasta t = 10s está dada por s = 4t + 1.6t2 - 0.08t3 m.
a) Determine la velocidad del bote y la aceleración en t = 4s.
b) ¿Cuál es la velocidad máxima del bote durante este intervalo de tiempo y cuándo
ocurre?