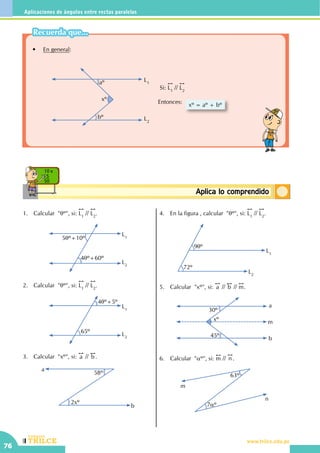
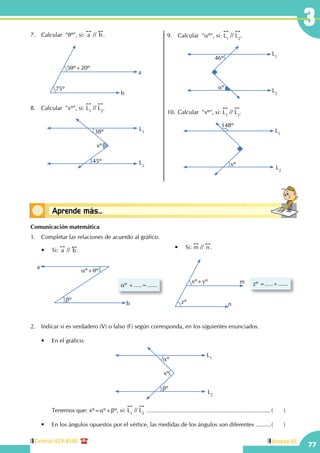
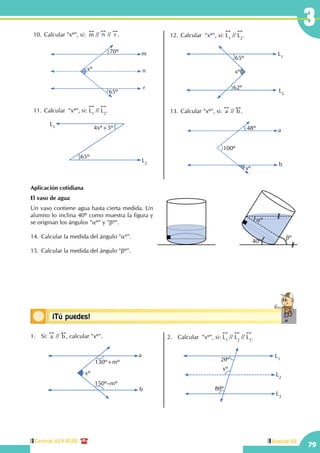
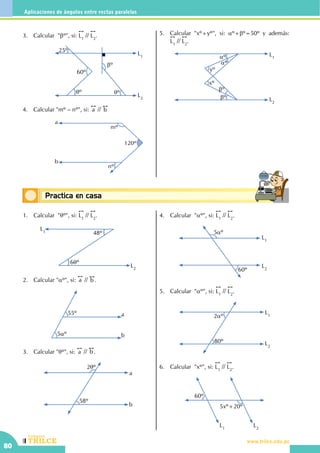
Este documento presenta un libro de texto sobre geometría dividido en varias unidades y capítulos. La unidad I introduce conceptos básicos como puntos, rectas, planos y figuras geométricas. La unidad II cubre ángulos. Las unidades III a VI se enfocan en temas específicos como rectas paralelas, triángulos, perímetros y áreas. Las unidades VII y VIII tratan sobre regiones poligonales, áreas y sólidos geométricos.



































![Geometría
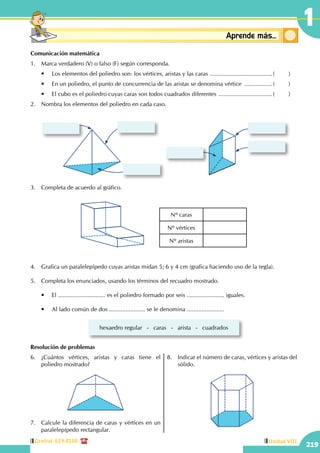
Central: 619-8100
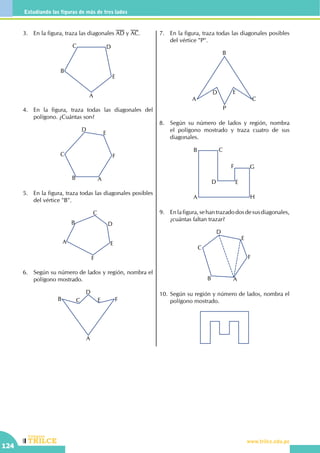
49
Unidad II
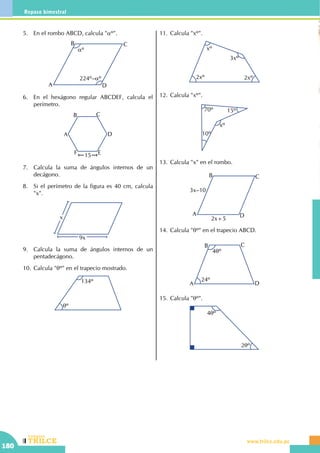
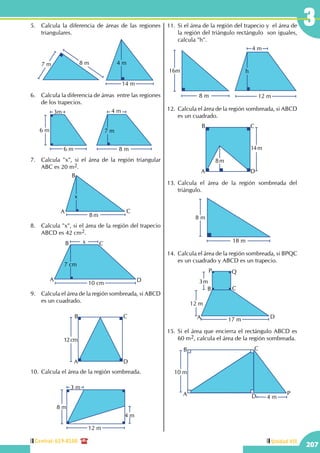
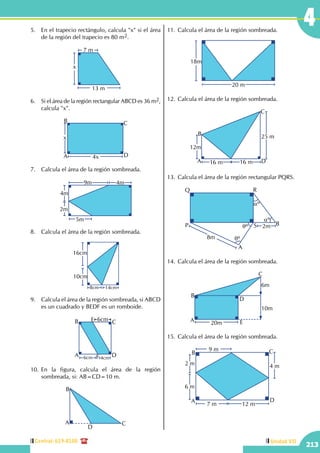
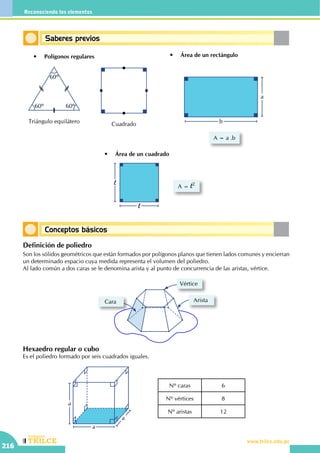
Conceptos básicos
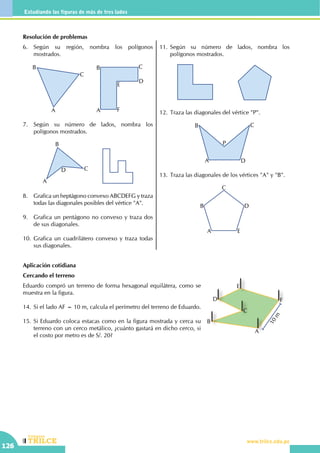
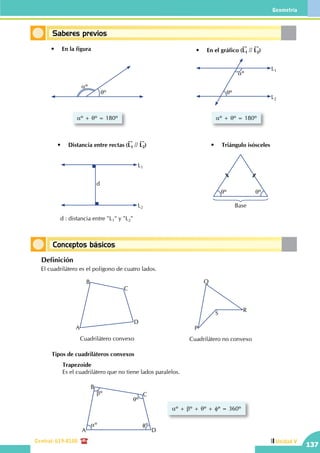
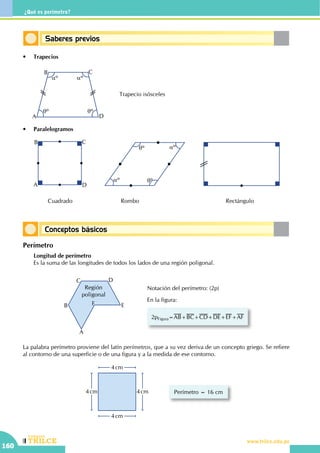
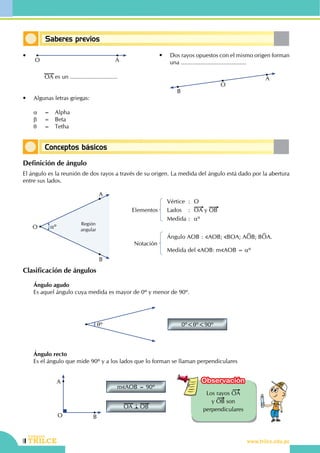
Saberes previos
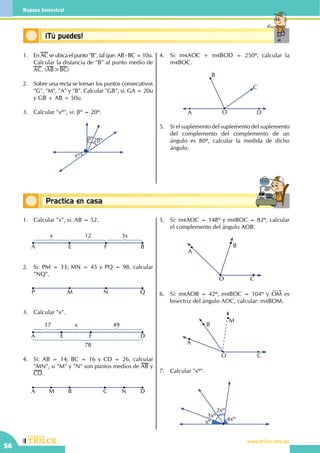
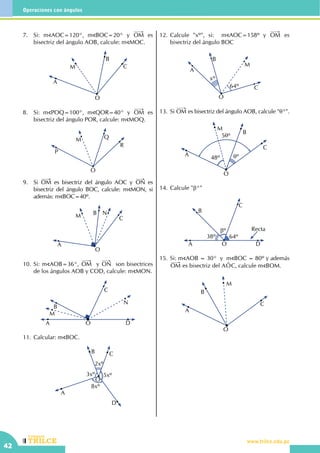
• El ángulo recto AOB mide ......................
O
A
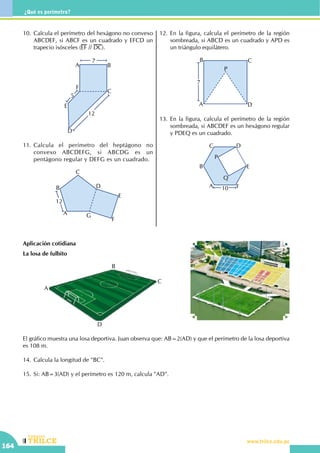
B
• Una recta se grafica idénticamente a un ángulo
180º
• 5 – [12 + (8 - 2)] = ...........................................
16 – [24 – (12 – 5)] = ...........................................
2x – [6x + 10x – (6x – 3x)] = ...........................................
18a – [12a – 3(4a – a)] = ...........................................
.............................................
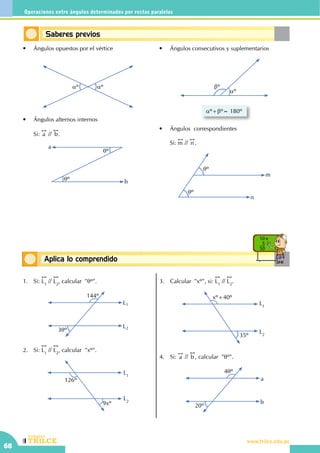
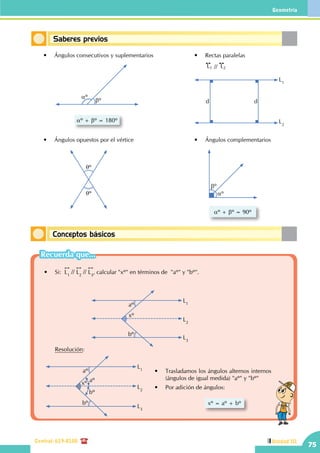
Definición de ángulos complementarios
Son aquellos dos ángulos cuyas medidas suman 90º.
O
A
αº
B
E
H
F
θº
αº + θº = 90º
Los ángulos AOB y EFH son complementarios.
Definición de ángulos suplementarios
Son aquellos dos ángulos cuyas medidas suman 180º.
Φº + ωº = 180º
P
ωº
R
Q
Φº
N
M
O
Los ángulos MON y RPQ son suplementarios](https://image.slidesharecdn.com/geometra2-150317180157-conversion-gate01/85/Geometria-2-49-320.jpg)