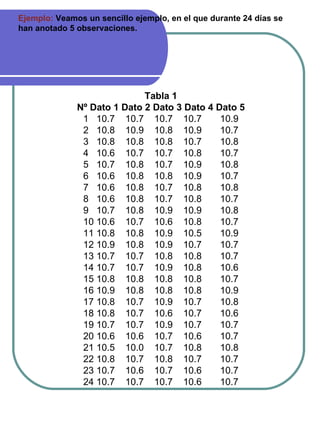
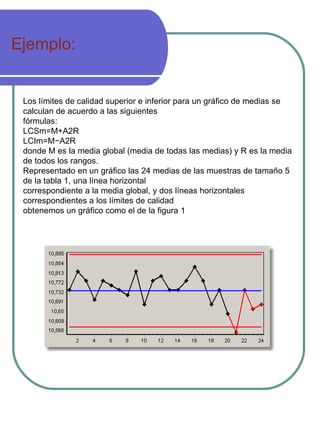
El documento explica los histogramas de frecuencia y los gráficos de control. Los histogramas son gráficos que representan la distribución de una variable mediante barras cuya anchura corresponde a intervalos de valores y cuya altura representa las frecuencias. Los gráficos de control se usan para monitorear procesos mediante el seguimiento de indicadores a lo largo del tiempo y detectar desviaciones respecto a los límites de control establecidos. El documento incluye un ejemplo numérico para ilustrar el cálculo e interpretación de un

1. HISTOGRAMAS DE FRECUENCIA En estadística , un histograma es una representación gráfica de una variable en forma de barras, donde la superficie de cada barra es proporcional a la frecuencia de los valores representados. En el eje vertical se representan las frecuencias, y en el eje horizontal los valores de las variables, normalmente señalando las marcas de clase, es decir, la mitad del intervalo en el que están agrupados los datos

2. Pasos para la construcción de un histograma de frecuencia Paso 1 Determinar el rango de los datos. Rango es igual al dato mayor menos el dato menor. Paso 2 Obtener el números de clases, existen varios criterios para determinar el número de clases (o barras) -por ejemplo la regla de Sturgess -. Sin embargo ninguno de ellos es exacto. Algunos autores recomiendan de cinco a quince clases, dependiendo de cómo estén los datos y cuántos sean. Un criterio usado frecuentemente es que el número de clases debe ser aproximadamente a la raíz cuadrada del número de datos. Por ejemplo, la raíz cuadrada de 30 ( número de artículos) es mayor que cinco, por lo que se seleccionan seis clases.

3. Pasos para la construcción de un histograma de frecuencia Paso 3 Establecer la longitud de clase: es igual al rango entre el número de clases. Paso 4 Construir los intervalos de clases: Los intervalos resultan de dividir el rango de los datos en relación al resultado del PASO 2 en intervalos iguales . Paso 5 Graficar el histograma: En caso de que las clases sean todas de la misma amplitud, se hace un gráfico de barras, las bases de las barras son los intervalos de clases y altura son la frecuencia de las clases. Si se unen los puntos medios de la base superior de los rectángulos se obtiene el polígono de frecuencias.

4. GRAFICOS DE CONTROL Los gráficos de control fueron propuesto originalmente por W. Shewart en 1920, y en ellos se representa a lo largo del tiempo el estado del proceso que estamos monitorizando. En el eje horizontal X se indica el tiempo, mientras que el eje vertical Y se representa algún indicador de la variable cuya calidad se mide. Además se incluye otras dos líneas horizontales: los límites superior e inferior de control , escogidos éstos de tal forma que la probabilidad de que una observación esté fuera de esos límites sea muy baja si el proceso está en estado de control , habitualmente inferior a 0.01 . La finalidad de los gráficos de control es por tanto monitorizar dicha situación para controlar su buen funcionamiento, y detectar rápidamente cualquier anomalía respecto al patrón correcto, puesto que ningún proceso se encuentra espontáneamente en ese estado de control, y conseguir llegar a él supone un éxito, así como mantenerlo; ése es el objetivo del control de calidad de procesos, y su consecución y mantenimiento exige un esfuerzo sistemático, en primer lugar para eliminar las causas asignables y en segundo para mantenerlo dentro de los estándares de calidad fijados.

5. Ejemplo: Veamos un sencillo ejemplo, en el que durante 24 días se han anotado 5 observaciones. Tabla 1 Nº Dato 1 Dato 2 Dato 3 Dato 4 Dato 5 1 10.7 10.7 10.7 10.7 10.9 2 10.8 10.9 10.8 10.9 10.7 3 10.8 10.8 10.8 10.7 10.8 4 10.6 10.7 10.7 10.8 10.7 5 10.7 10.8 10.7 10.9 10.8 6 10.6 10.8 10.8 10.9 10.7 7 10.6 10.8 10.7 10.8 10.8 8 10.6 10.8 10.7 10.8 10.7 9 10.7 10.8 10.9 10.9 10.8 10 10.6 10.7 10.6 10.8 10.7 11 10.8 10.8 10.9 10.5 10.9 12 10.9 10.8 10.9 10.7 10.7 13 10.7 10.7 10.8 10.8 10.7 14 10.7 10.7 10.9 10.8 10.6 15 10.8 10.8 10.8 10.8 10.7 16 10.9 10.8 10.8 10.8 10.9 17 10.8 10.7 10.9 10.7 10.8 18 10.8 10.7 10.6 10.7 10.6 19 10.7 10.7 10.9 10.7 10.7 20 10.6 10.6 10.7 10.6 10.7 21 10.5 10.0 10.7 10.8 10.8 22 10.8 10.7 10.8 10.7 10.7 23 10.7 10.6 10.7 10.6 10.7 24 10.7 10.7 10.7 10.6 10.7

6. Ejemplo: Para elaborar el gráfico de evolución de medias, en primer lugar se calcula la media de cada muestra de 5 observaciones y luego la media global de esas 24 medias. Seguidamente se calcula los rangos para cada muestra (valor máximo − valor mínimo), así como la media de los 24 rangos. Para el cálculo de los límites de control se utiliza la teoría de probabilidades, suponiendo que los datos siguen una determinada distribución de probabilidad, ya sea ésta normal, binomial, Poisson o cualquiera otra, dependiendo del tipo de datos analizado. De esta forma se determinará un factor que al multiplicarlo por un parámetro de variabilidad (sea éste el rango o la desviación típica) nos permite calcular los límites del gráfico de control de calidad, límites que nos garantizan una probabilidad del 99 % de que las observaciones se encuentren dentro de esos márgenes si el proceso está en estado de control. Es un concepto totalmente análogo al de intervalo de confianza para una estimación, al que estamos habituados en la inferencia estadística.

7. Ejemplo: Los límites de calidad superior e inferior para un gráfico de medias se calculan de acuerdo a las siguientes fórmulas: LCSm=M+A2R LCIm=M−A2R donde M es la media global (media de todas las medias) y R es la media de todos los rangos. Representado en un gráfico las 24 medias de las muestras de tamaño 5 de la tabla 1, una línea horizontal correspondiente a la media global, y dos líneas horizontales correspondientes a los límites de calidad obtenemos un gráfico como el de la figura 1