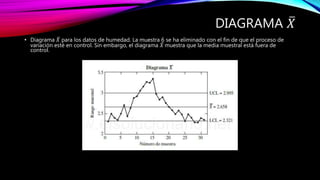
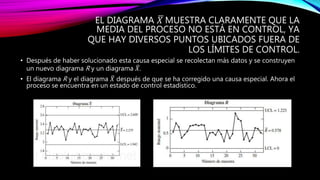
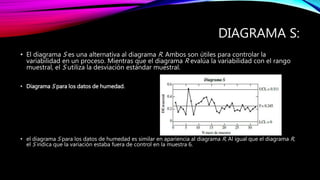
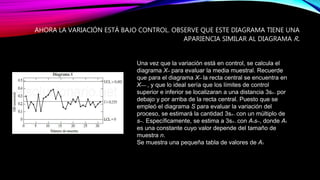
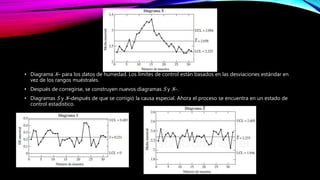
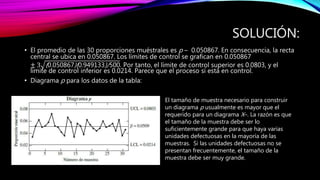
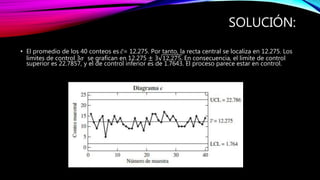
Este documento proporciona una introducción al control estadístico de calidad. Explica qué son las variables y atributos, y describe los diagramas de control como herramientas para determinar si un proceso está bajo control. Detalla los diagramas de control de variables como el diagrama X, R y S, y los diagramas de control de atributos como el diagrama p. Incluye ejemplos para ilustrar cómo construir y utilizar estos diagramas.

1. CONTROL ESTADÍSTICO DE
CALIDAD
Díaz Venegas Ma. Alejandra
Gutiérrez De la Cruz Fabiola
Vázquez López Francisco Enrique

2. INTRODUCCIÓN
• La forma mas eficaz para mantener una alta calidad, es el seguimiento del proceso
de producción, realizar pruebas, la cual estas pruebas se realizan mediante la
extracción de una muestra grande en el proceso de producción. Uno de los
pioneros en el área del control de calidad estadístico fue el doctor Walter A.
Shewart, de los laboratorios de la compañía telefónica Bell. En 1924 desarrolló la
gráfica del control moderna, sigue siendo una de las herramientas mas utilizadas en
la industria.

3. CONTENIDO:
• ¿Qué es una variable?
• ¿Qué es un atributo?
• ¿Qué es un diagrama de control?
• Diagramas de control de variable (X, R, y S)
• Diagramas de control de atributos
• Ejemplos

4. ¿QUÉ ES UNA VARIABLE?
• Las variables, también suelen ser llamados caracteres cuantitativos, son aquellos que
pueden ser expresados mediante números. Son caracteres susceptibles de medición.
Como por ejemplo, la estatura, el peso, el salario, la edad, etc.

5. ¿QUÉ ES UNA ATRIBUTO?
• Los atributos también llamados caracteres cualitativos, son aquellos que no son
susceptibles de medición, es decir que no se pueden expresar mediante un número.

6. ¿QUÉ ES UN DIAGRAMA DE
CONTROL?
• Los diagramas de control ayudan a la persona a cargo, en la mayoría de los casos,
al ingeniero responsable del mismo decidir si un proceso parece estar en control, o
si están presente una o más causas especiales.
• Si se determina que el proceso está fuera de control, debe definirse y corregirse la
naturaleza de la causa especial, de tal forma que el proceso vuelva al estado de
control estadístico. Existen diversos tipos de diagramas de control.

7. • Dependiendo del diagrama de control utilizado en los procesos, será esta la
característica de calidad con la que se mido una:
• Variable continua.
• Variable binaria.
• Variable discreta.

8. EJEMPLO:
• Cuando se hace el seguimiento de un proceso que fabrica latas de aluminio para bebidas,
debe medirse la altura de cada lata de la muestra. La altura es una variable continua.
• En ciertas ocasiones, basta simplemente con determinar si la altura se encuentra dentro
de ciertos límites requeridos. En este caso, la medición de la calidad toma sólo uno de los
dos valores: adecuado (dentro de los límites) o no adecuado (fuera de los límites). Esta
medición es una variable binaria, ya que sólo tiene dos valores.
• Finalmente, podría tenerse interés en contar el número de imperfecciones en la superficie
de la lata. Ésta es una variable discreta.

9. • A los diagramas de control que se usan para las variables continuas se llaman
diagramas de control de variables. Existiendo tres ejemplos:
• El diagrama 𝑋
• El diagrama R
• El diagrama S
• A los diagramas de control que se usan para las variables binarias o discretas se
les llama diagramas de control de atributos.
• El diagrama p es el diagrama mas comúnmente utilizado para variables binarias.
• El diagrama c se utiliza para las variables discretas.

10. RECOLECCIÓN DE DATOS:
SUBGRUPOS RACIONALES
• Los datos utilizados en la construcción de un diagrama de control se recolectan
mediante cierto número de muestras tomadas durante determinado periodo. A
estas muestras se les conoce como subgrupos racionales.

11. • Los dos métodos comúnmente más utilizados son:
1. Muestreo en intervalos regulares, en el que todos los elementos de cada
muestra son producidos casi en el mismo tiempo en que se realiza el
muestreo.
2. Muestreo en intervalos regulares, en el que los elementos de cada
muestra se extraen a partir de todas las unidades producidas desde que
se tomó la última muestra.

12. DIAGRAMAS DE CONTROL DE
VARIABLES
• Cuando se realiza una medición de calidad en una escala de variables, a los datos se
les conoce como datos de variables. Primero se utiliza un diagrama R o un diagrama
S con el fin de controlar la variabilidad del proceso, y después se utiliza un diagrama
X– para controlar la media del proceso.

13. EJEMPLO:
• Un ingeniero de control de calidad a cargo de un proceso de empaquetado de sal está preocupado por el
contenido de humedad en los paquetes de sal. Para determinar si el proceso está en control estadístico,
primero se necesitan definir los subgrupos racionales, y después recolectar ciertos datos. Suponga que
para el proceso de empaquetado de sal la preocupación principal es que la variación en la humedad del
ambiente de la planta pueda variar el contenido de humedad promedio de los paquetes a lo largo del
tiempo. Recuerde que los subgrupos racionales deben elegirse de tal forma que la variación dentro de
cada muestra se deba sólo a causas comunes, no a causas especiales. Por consiguiente, en este caso una
buena opción para los subgrupos racionales es extraer muestras de diversos paquetes, cada una en
intervalos regulares. Los paquetes en cada muestra serán producidos lo más próximos en tiempo entre sí.
De este modo, la humedad del ambiente será casi la misma para cada paquete de la muestra, de forma
que la variación dentro del grupo no se verá afecta por esta causa especial. Suponga que se extraen cinco
paquetes de sal cada 15 minutos durante ocho horas, y que el contenido de humedad en cada paquete se
mide como un porcentaje del peso total. Los datos se presentan en la tabla

14. CONTENIDO DE HUMEDAD EN LOS PAQUETES DE
SAL, COMO PORCENTAJE DEL PESO TOTAL
• control es que cada valor de 𝑋 se aproxima a
la media del proceso durante el tiempo en
que se tomó la muestra, mientras que los
valores de R y s se pueden utilizar para
aproximar la desviación estándar muestra.
• Si el proceso está en control, entonces la
media y la desviación estándar del proceso
son iguales en cada muestra. Si el proceso
está fuera de control, la media del proceso m
o la desviación estándar s, o ambas, diferirán
de muestra en muestra. Por tanto, los valores
de X–, R, y s variarán menos cuando el
proceso esté en control que cuando el
proceso esté fuera de control.

15. DIAGRAMA R PARA DATOS DE
HUMEDAD.
• Presenta el diagrama R para los datos
de humedad. El eje horizontal
representa las muestras, numeradas del
1 al 32. Los rangos muéstrales están
graficados en el eje vertical. Las tres
líneas horizontales son las más
importantes. La recta en el centro del
diagrama es el valor R – y se le llama
recta central. Las rectas superior e
inferior indican los límites de control 3σ
superior e inferior (UCL y LCL,
respectivamente). Los límites de control
están dibujados de tal forma que
cuando el proceso está en control, casi
todos los puntos estarán dentro de los
límites. Un punto graficado fuera de los
límites de control es una evidencia de
que el proceso no está en control.

16. • Se puede demostrar mediante métodos avanzados que las cantidades mR 3sR. pueden
estimarse con múltiplos de R – ; dichos múltiplos se representan con D3 y D4. La cantidad
mR 3sR. se estima con D3R – , y la cantidad mR 3sR. se estima con D4R – . Las cantidades
D3 y D4 son constantes cuyos valores dependen del tamaño de la muestra n.

17. LA FIGURA DE LA DIAPOSITIVA 15 MUESTRA QUE EL RANGO PARA LA MUESTRA 6
EXCEDE EL LÍMITE DE CONTROL SUPERIOR, POR LO QUE EVIDENCIA QUE ESTABA
OPERANDO UNA CAUSA ESPECIAL Y QUE LA VARIACIÓN DEL PROCESO NO ESTÁ
EN CONTROL. LA ACCIÓN APROPIADA ES DETERMINAR LA NATURALEZA DE LA
CAUSA ESPECIAL, Y DESPUÉS ELIMINAR LA MUESTRA QUE NO ESTÁ EN CONTROL Y
CALCULAR DE NUEVO LOS LÍMITES.
• Se elimina la muestra 6 de los datos
y se vuelve a calcular el diagrama R.
Los resultados se muestran en la
figura de la diapositiva Ahora, la
variación del proceso está en control.

18. DIAGRAMA 𝑋
• Diagrama 𝑋 para los datos de humedad. La muestra 6 se ha eliminado con el fin de que el proceso de
variación esté en control. Sin embargo, el diagrama 𝑋 muestra que la media muestral está fuera de
control.

19. LA RECTA CENTRAL SE UBICA EN 𝑋 LA CANTIDAD 𝜎 𝑋 SE PUEDE ESTIMAR YA SEA MEDIANTE EL RANGO
PROMEDIO R O USANDO LAS DESVIACIONES ESTÁNDAR MUÉSTRALES. AQUÍ SE USARÁ R Y AL FINAL DE LA
SECCIÓN SE ANALIZARÁN LOS MÉTODOS BASADOS EN LA DESVIACIÓN ESTÁNDAR, JUNTO CON EL ANÁLISIS
DE LOS DIAGRAMAS S. SE PUEDE DEMOSTRAR POR MEDIO DE MÉTODOS AVANZADOS QUE LA CANTIDAD
3𝜎 𝑋 SE ESTIMA CON A2 𝑅 , DONDE A2 ES UNA CONSTANTE CUYO VALOR DEPENDE DEL TAMAÑO DE LA
MUESTRA. A CONTINUACIÓN SE PRESENTA UNA TABLA DE VALORES DE A2.

20. EL DIAGRAMA 𝑋 MUESTRA CLARAMENTE QUE LA
MEDIA DEL PROCESO NO ESTÁ EN CONTROL, YA
QUE HAY DIVERSOS PUNTOS UBICADOS FUERA DE
LOS LÍMITES DE CONTROL.
• Después de haber solucionado esta causa especial se recolectan más datos y se construyen
un nuevo diagrama R y un diagrama 𝑋.
• El diagrama R y el diagrama 𝑋 después de que se ha corregido una causa especial. Ahora el
proceso se encuentra en un estado de control estadístico.

21. DIAGRAMA S:
• El diagrama S es una alternativa al diagrama R. Ambos son útiles para controlar la
variabilidad en un proceso. Mientras que el diagrama R evalúa la variabilidad con el rango
muestral, el S utiliza la desviación estándar muestral.
• Diagrama S para los datos de humedad.
• el diagrama S para los datos de humedad es similar en apariencia al diagrama R, Al igual que el diagrama R,
el S indica que la variación estaba fuera de control en la muestra 6.

22. • suponga que 32 desviaciones estándar provienen de una población con media 𝜇 y
desviación estándar 𝜎. Idealmente se desearía que en el diagrama la recta central
estuviera en 𝜇s y los límites de control en 𝜇s±3𝜎s. Generalmente no se conocen estas
cantidades. Se aproxima 𝜇s con 𝑆, el promedio de las desviaciones estándar. Por tanto, se
grafica la recta central en 𝑆. Puede demostrarse mediante métodos avanzados que las
cantidades 𝜇s±3𝜎s pueden estimarse con múltiplos de 𝑆; estos múltiplos se representan
mediante B3 y B4. La cantidad 𝜇s−3𝜎s se estima con B3 𝑆, mientras que la cantidad
𝜇s+3𝜎s se estima con B4 𝑆. Las cantidades B3 y B4 son constantes cuyos valores depende
n del tamaño de la muestra n.
• tabla de valores de B3 y B4.
La variación del proceso se encuentra fuera
de control en la muestra 6. Se elimina esta
muestra y se vuelve a calcular el diagrama S.

23. AHORA LA VARIACIÓN ESTÁ BAJO CONTROL. OBSERVE QUE ESTE DIAGRAMA TIENE UNA
APARIENCIA SIMILAR AL DIAGRAMA R.
Una vez que la variación está en control, se calcula el
diagrama X– para evaluar la media muestral. Recuerde
que para el diagrama X– la recta central se encuentra en
X–– , y que lo ideal sería que los límites de control
superior e inferior se localizaran a una distancia 3sX— por
debajo y por arriba de la recta central. Puesto que se
empleó el diagrama S para evaluar la variación del
proceso, se estimará la cantidad 3sX— con un múltiplo de
s–. Específicamente, se estima a 3sX— con A3s–, donde A3
es una constante cuyo valor depende del tamaño de
muestra n.
Se muestra una pequeña tabla de valores de A3

24. SE MUESTRA UNA PEQUEÑA TABLA DE VALORES DE A3.

25. • Diagrama X– para los datos de humedad. Los límites de control están basados en las desviaciones estándar en
vez de los rangos muéstrales.
• Después de corregirse, se construyen nuevos diagramas S y X–.
• Diagramas S y X–después de que se corrigió la causa especial. Ahora el proceso se encuentra en un estado de
control estadístico.

26. • El diagrama S es una alternativa al diagrama R que puede utilizarse junto con el
diagrama X–. Para los datos de humedad, los dos diagramas produjeron
resultados muy similares. Esto es cierto en muchos casos, pero algunas veces los
resultados son diferentes.

27. DIAGRAMAS DE CONTROL DE
ATRIBUTOS
• El diagrama p se utiliza cuando la característica de calidad que se medirá en cada unidad
sólo toma dos valores; por lo general, “defectuoso” y “no defectuoso”. En cada muestra se
calcula la proporción de unidades defectuosas; después se grafican estas proporciones
muéstrales. Ahora se describirá cómo calcular la recta central y los límites de control. Sea p
la probabilidad de que una unidad dada esté defectuosa.

28. EJEMPLO: • En la producción de placas de silicio se extraen 30 muestras de tamaño 500, y
se calcula la proporción de placas defectuosas en cada muestra. La tabla 10.2
muestra los resultados. Calcule la recta central y los límites de control del
diagrama p. Dibuje el diagrama. ¿Parece que el proceso esté en control?

29. SOLUCIÓN:
• El promedio de las 30 proporciones muéstrales es p – 0.050867. En consecuencia, la recta
central se ubica en 0.050867. Los límites de control se grafican en 0.050867
± 3 (0.050867)(0.949133)/500. Por tanto, el límite de control superior es 0.0803, y el
límite de control inferior es 0.0214. Parece que el proceso sí está en control.
• Diagrama p para los datos de la tabla:
El tamaño de muestra necesario para construir
un diagrama p usualmente es mayor que el
requerido para un diagrama X–. La razón es que
el tamaño de la muestra debe ser lo
suficientemente grande para que haya varias
unidades defectuosas en la mayoría de las
muestras. Si las unidades defectuosas no se
presentan frecuentemente, el tamaño de la
muestra debe ser muy grande.

30. • El diagrama c se utiliza cuando la medida de calidad es el conteo del
número de defectos, o imperfecciones, en una unidad dada. Una unidad
puede ser un solo elemento o un grupo de elementos lo suficientemente
grande para que el número esperado de imperfecciones sea lo bastante
grande. El uso del diagrama c requiere que el número de defectos siga una
distribución Poisson.

31. EJEMPLO:
• Se examinan las grietas en la superficie de los rollos de laminas de
aluminio utilizados para fabricar latas, La tabla 10.3 presenta el
numero de grietas que hay en 40 muestras de 100 m2 cada un.
Calcule la recta y los limites de control 3𝜎 para el diagrama c.
dibuje el diagrama. ¿El proceso parece estar en control?

32. SOLUCIÓN:
• El promedio de los 40 conteos es 𝑐= 12.275. Por tanto, la recta central se localiza en 12.275. Los
limites de control 3𝜎 se grafican en 12.275 ± 3 12.275. En consecuencia, el limite de control
superior es 22.7857, y el de control inferior es de 1.7643. El proceso parece estar en control.

33. CONCLUSIÓN:
• Los diagramas no son inútiles para compararnos con la competencia, ver que esta
mal en nuestro proceso o que nos podría perjudicar en nuestra calidad del
producto, solucionando estos problemas y que el producto sea de primera o mejor
que la competencia