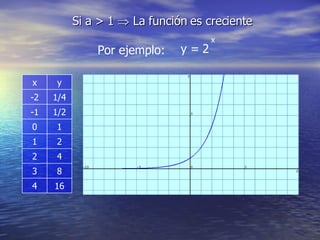
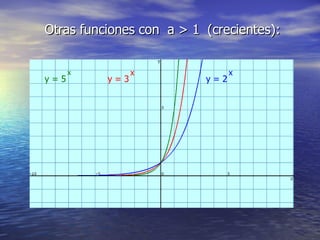
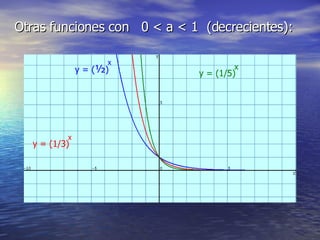
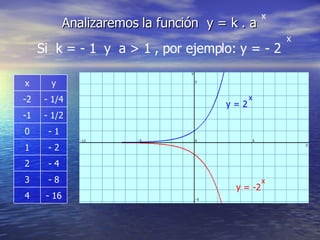
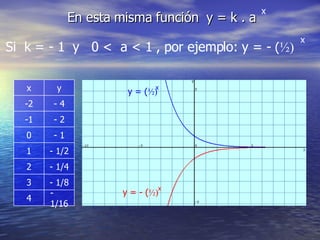
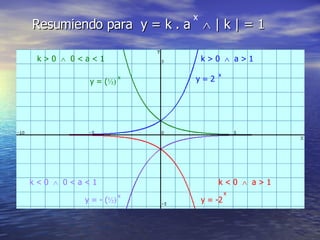
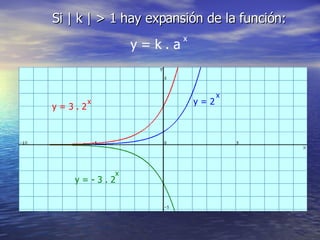
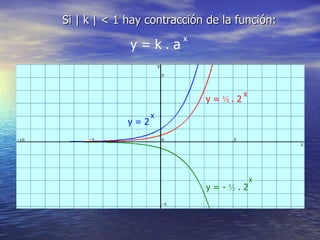
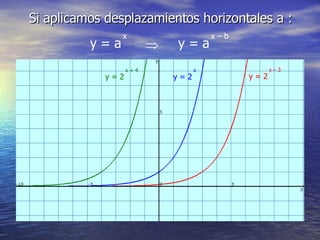
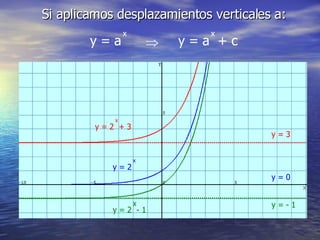
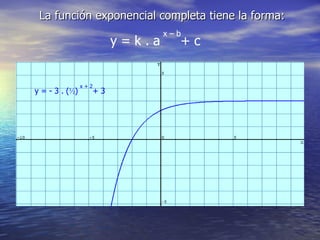
La función exponencial tiene la forma y = a^x. Si a > 1, la función es creciente, mientras que si 0 < a < 1, la función es decreciente. La función exponencial generalizada tiene la forma y = k*a^x, donde k y a determinan si la función es creciente o decreciente. Además, se pueden aplicar desplazamientos horizontales y verticales de la forma y = a^x - b y y = a + cx respectivamente.

1. Fatela Preuniversitarios Funciones Exponenciales

2. Función Exponencial La función exponencial tiene la forma:  a / a > 0  a  1 y = a x

3. Si a > 1  La función es creciente Por ejemplo: y = 2 x 16 4 8 3 4 2 2 1 1 0 1/2 -1 1/4 -2 y x

4. Si 0 < a < 1  La función es decreciente Por ejemplo: y = ( ½) x 1/16 4 1/8 3 1/4 2 1/2 1 1 0 2 -1 4 -2 y x

5. Otras funciones con a > 1 (crecientes): y = 2 x y = 3 x y = 5 x

6. Otras funciones con 0 < a < 1 (decrecientes): y = ( ½ ) x y = (1/3) x y = (1/5) x

7. Analizaremos la función y = k . a x Si k = - 1 y a > 1 , por ejemplo: y = - 2 y = 2 x y = -2 x x - 16 4 - 8 3 - 4 2 - 2 1 - 1 0 - 1/2 -1 - 1/4 -2 y x

8. En esta misma función y = k . a x Si k = - 1 y 0 < a < 1 , por ejemplo: y = - ( ½) x y = ( ½) x y = - ( ½) x - 1/16 4 - 1/8 3 - 1/4 2 - 1/2 1 - 1 0 - 2 -1 - 4 -2 y x

9. Resumiendo para y = k . a  | k | = 1 x k > 0  a > 1 k > 0  0 < a < 1 k < 0  a > 1 k < 0  0 < a < 1 y = 2 x y = -2 x y = ( ½) x y = - ( ½) x

10. Si | k | > 1 hay expansión de la función: y = k . a x y = 2 x y = - 3 . 2 x y = 3 . 2 x

11. Si | k | < 1 hay contracción de la función: y = k . a x y = 2 x y = - ½ . 2 x y = ½ . 2 x

12. Si aplicamos desplazamientos horizontales a : y = a x y = a x – b  y = 2 x y = 2 x + 4 y = 2 x – 3

13. Si aplicamos desplazamientos verticales a: y = a x y = a + c x  y = 2 x y = 2 - 1 x y = 2 + 3 x y = 3 y = 0 y = - 1

14. La función exponencial completa tiene la forma: y = k . a + c x – b y = - 3 . ( ½ ) + 3 x + 2

15. Fin de la presentación