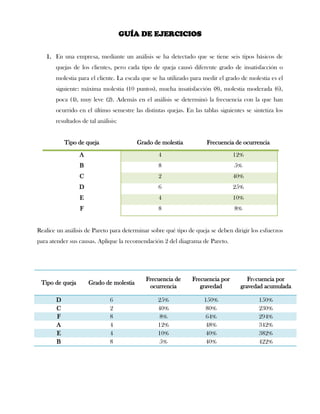
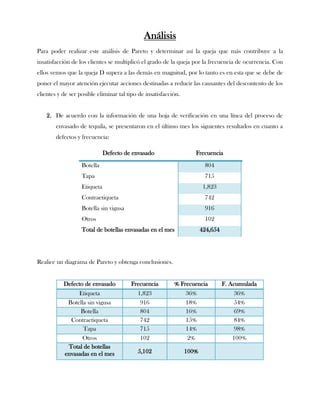
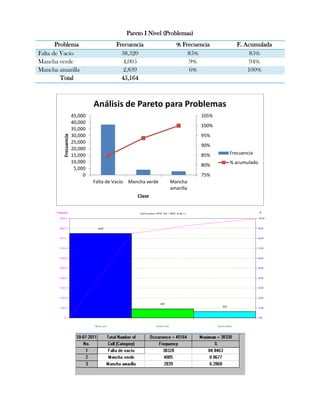
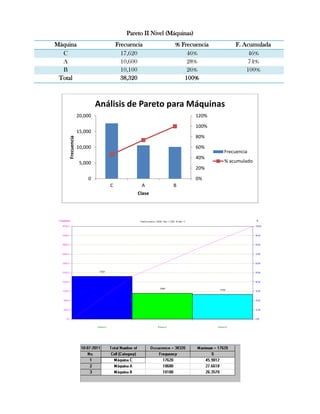
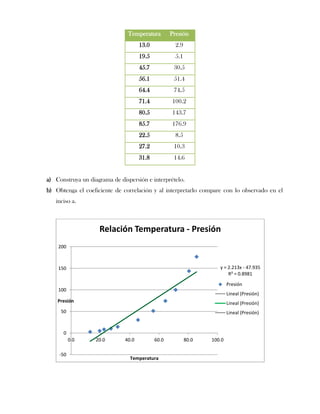
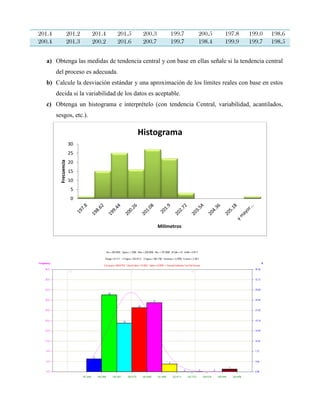
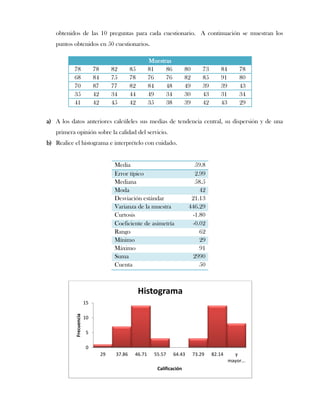
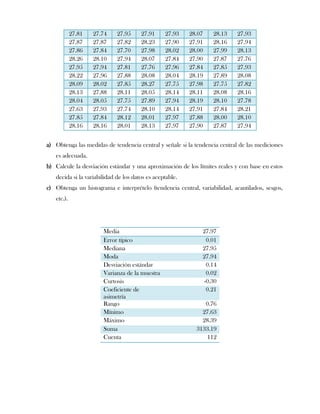
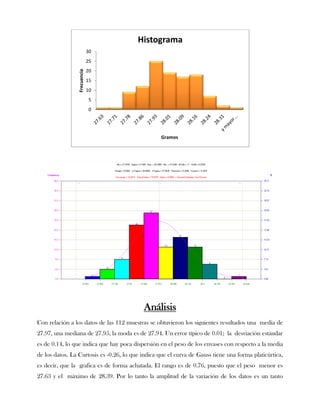
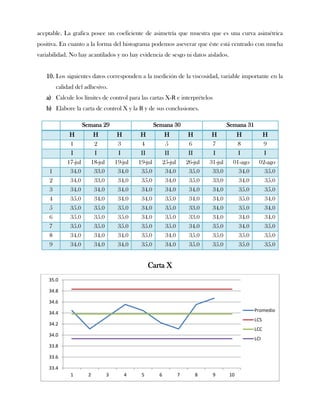
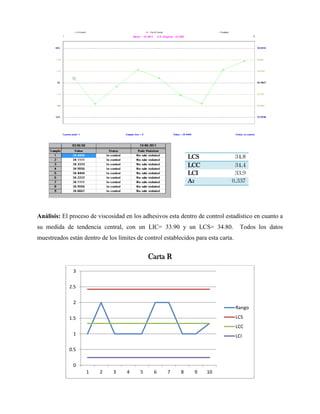
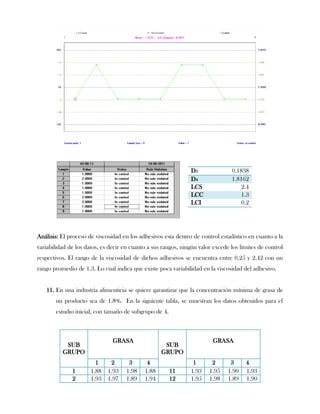
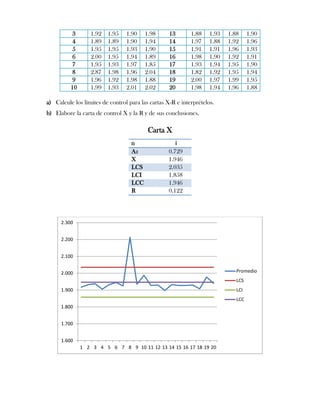
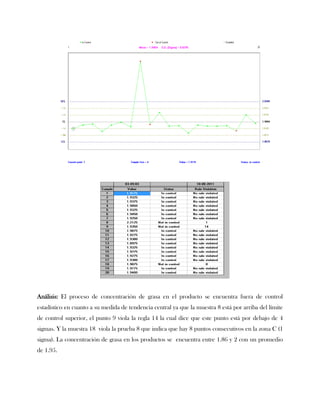
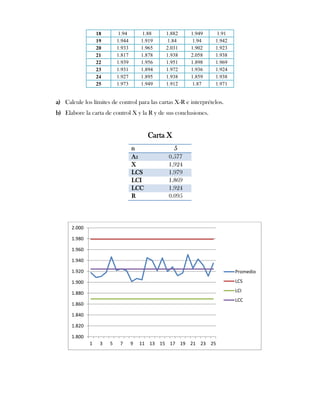
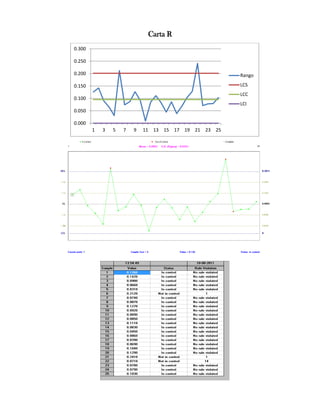
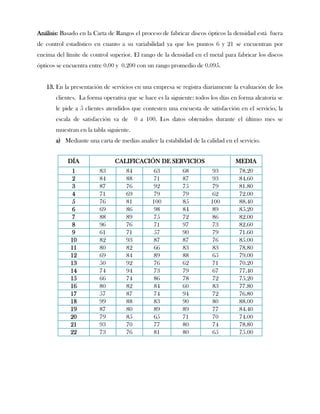
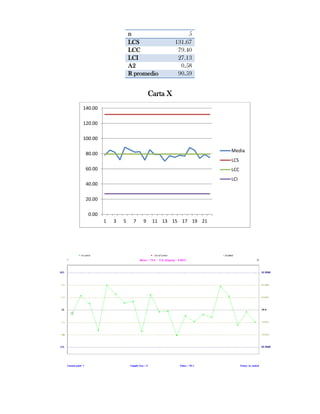
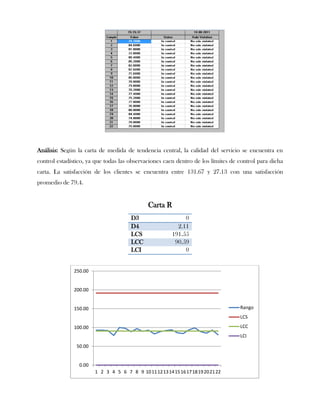
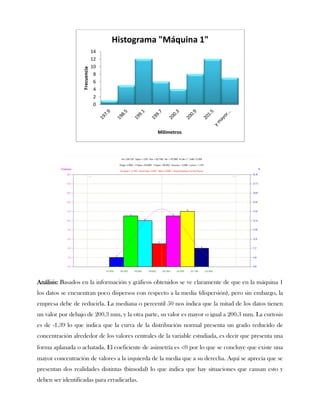
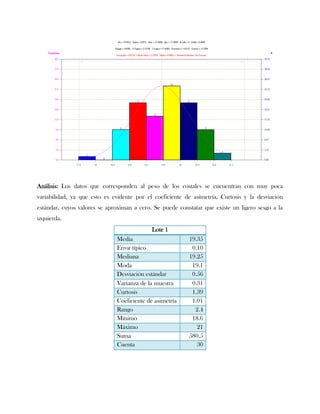
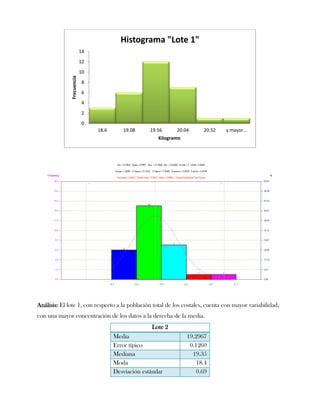
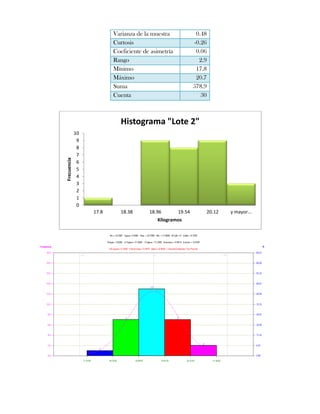
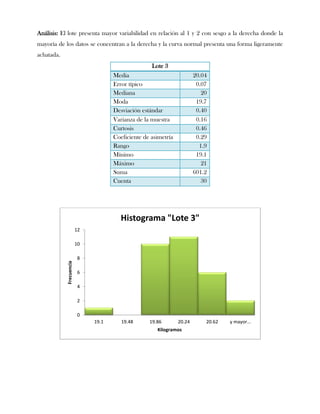
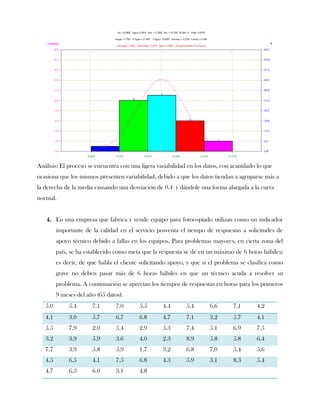
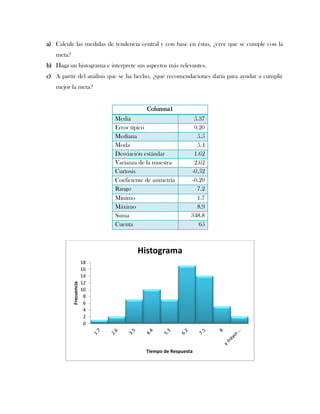
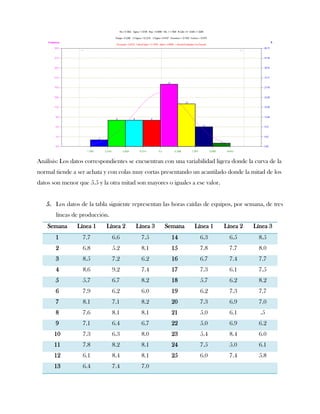
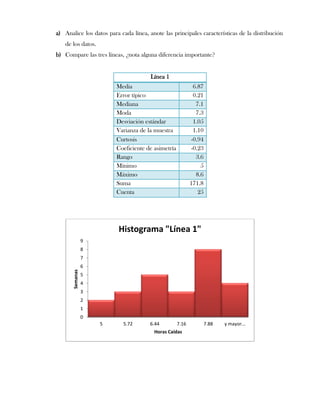
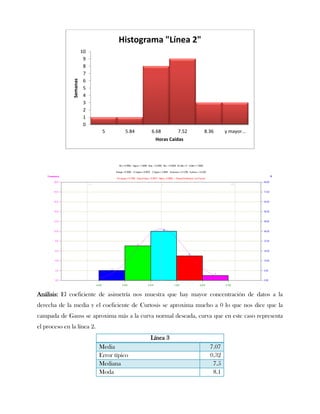
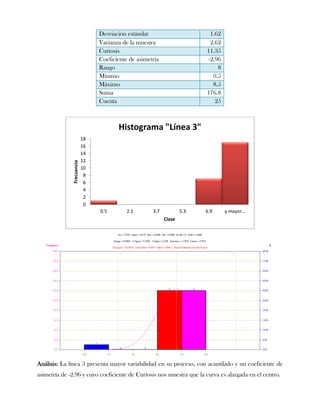
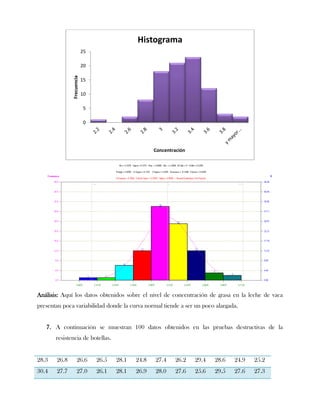
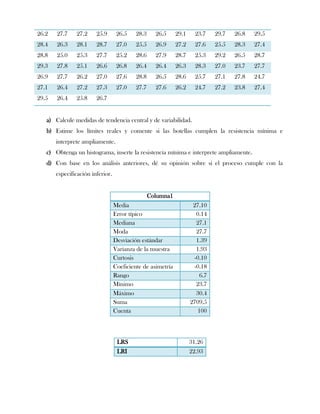
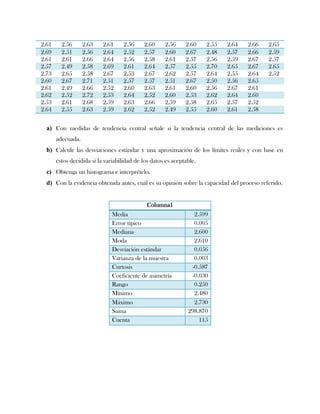
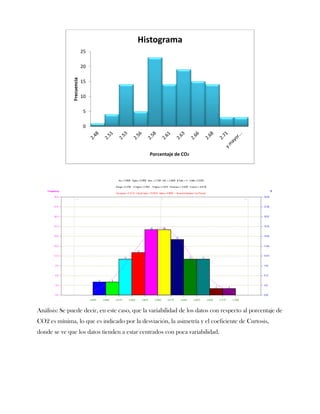
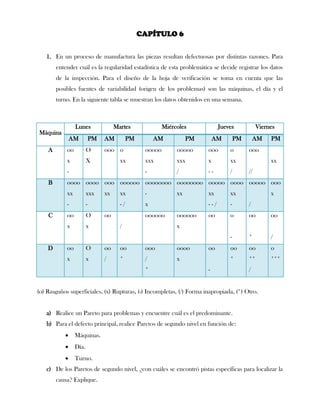
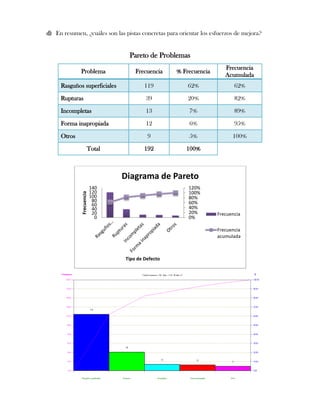
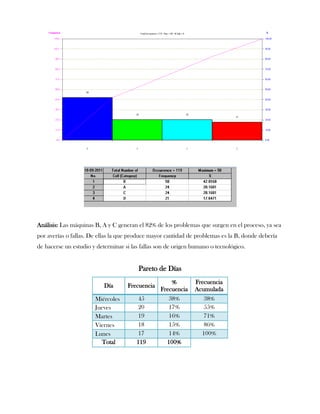
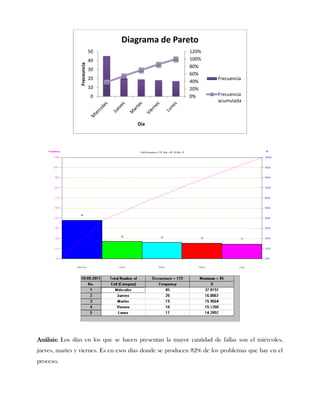
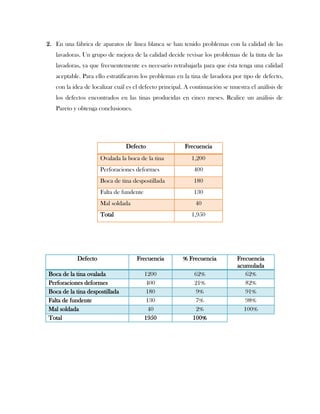
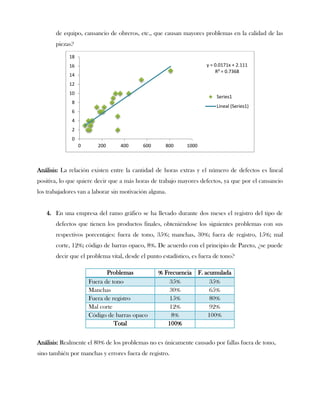
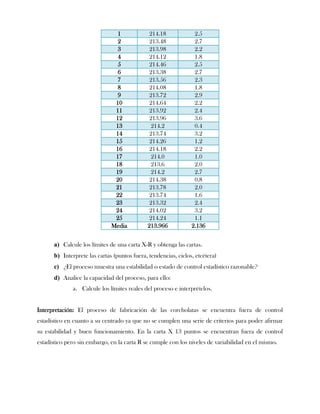
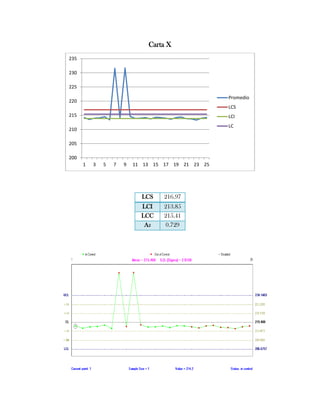
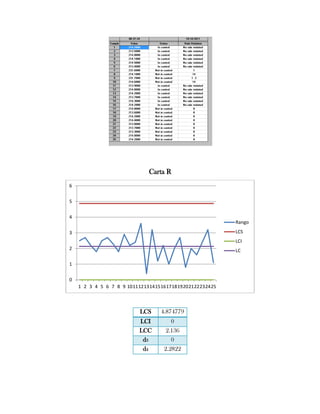
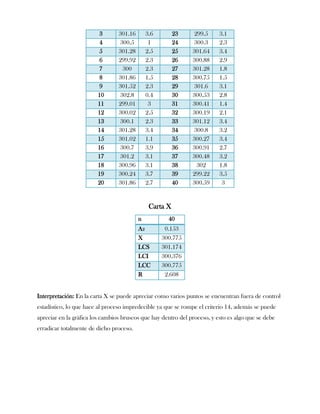
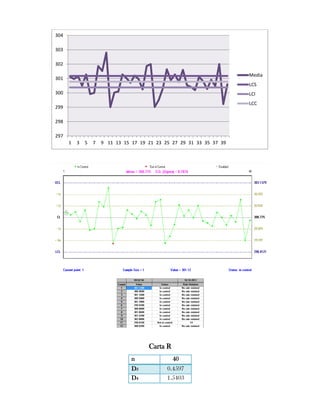
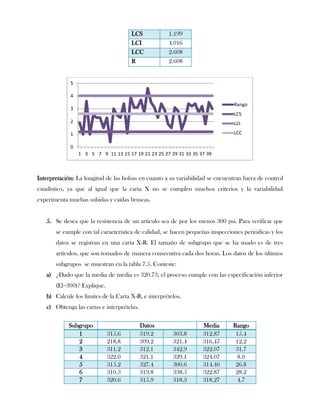
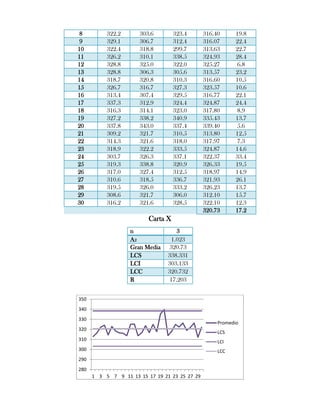
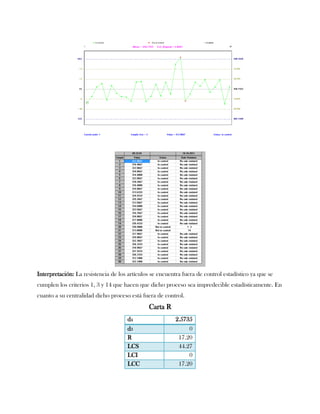
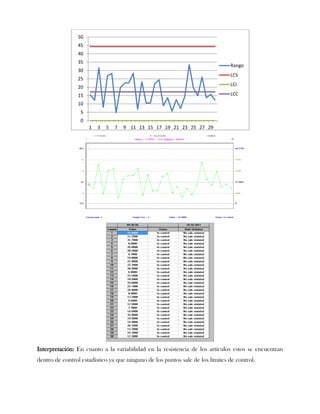
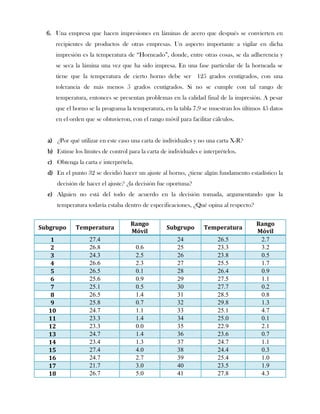
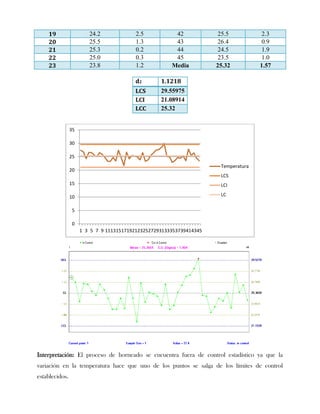
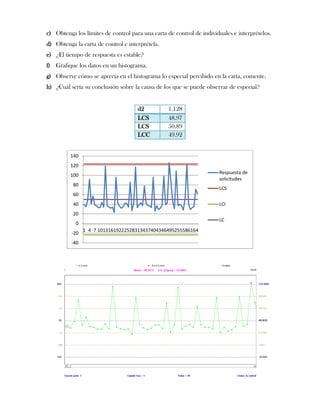
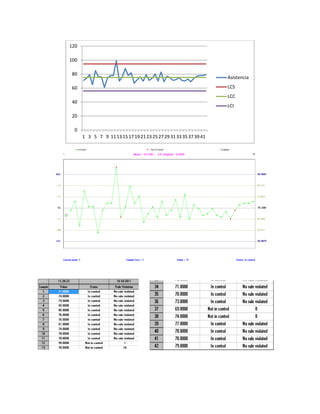
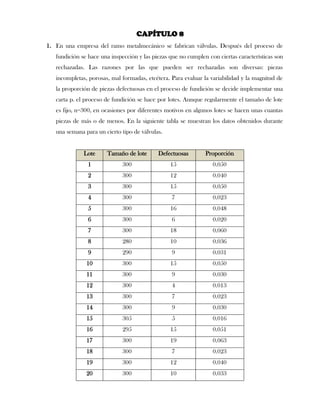
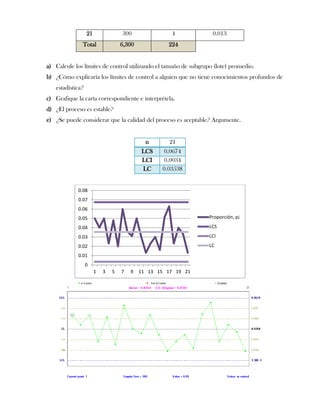
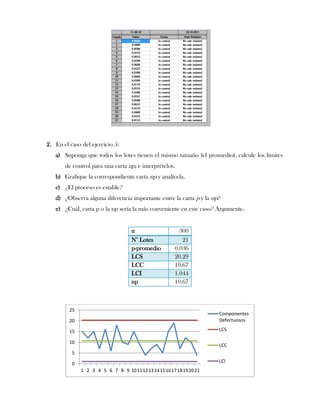
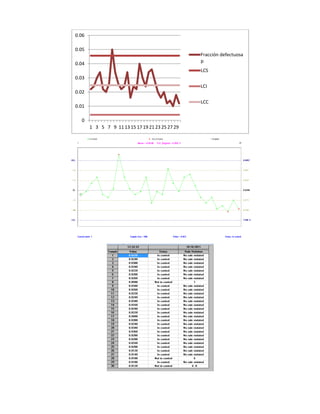
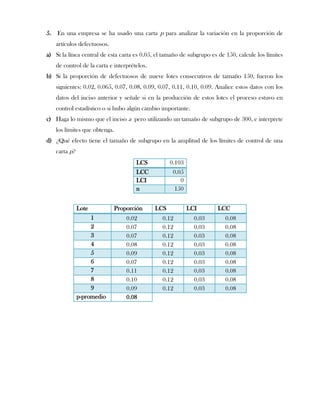
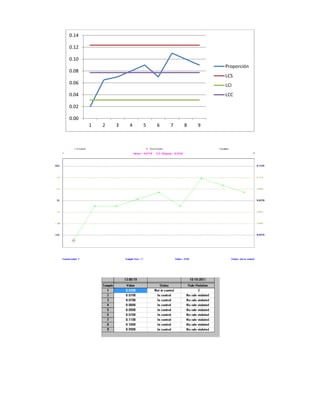
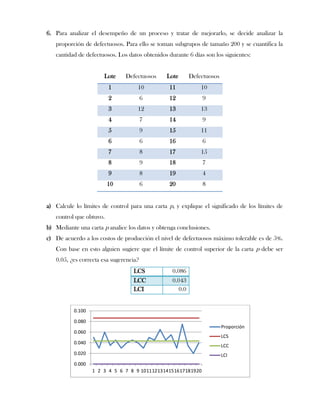
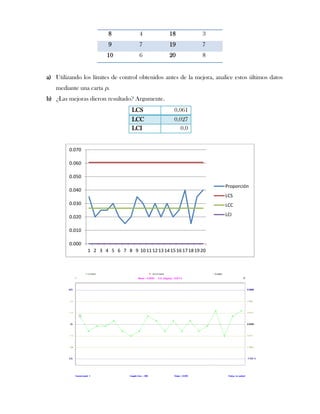
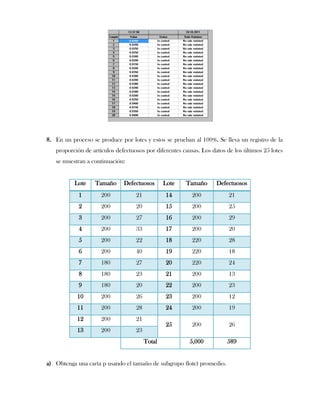
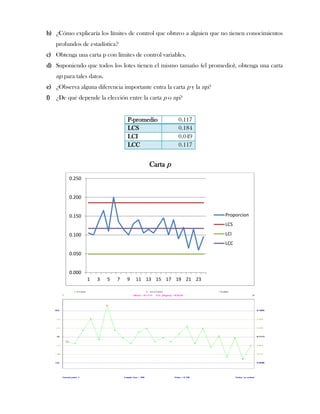
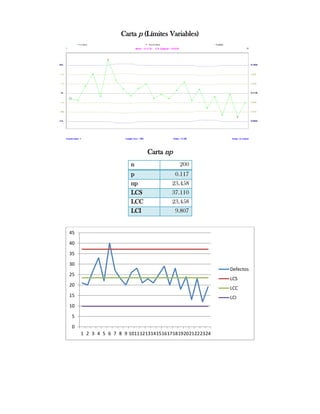
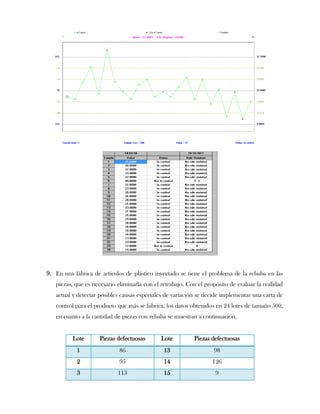
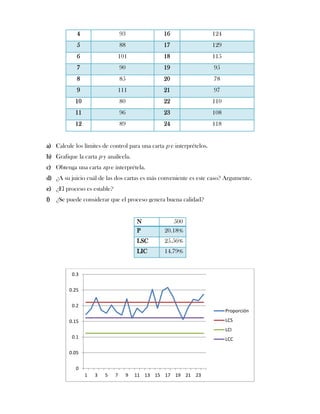
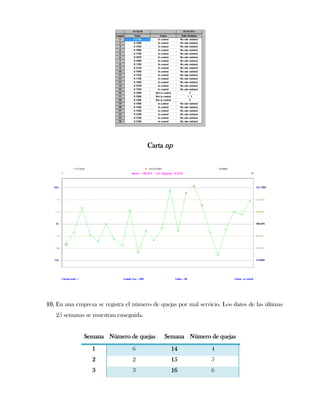
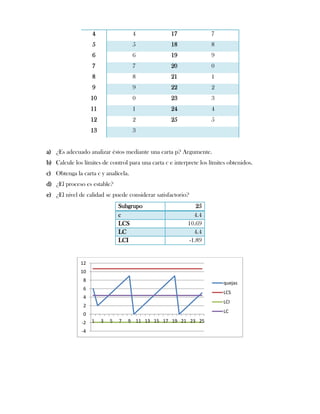
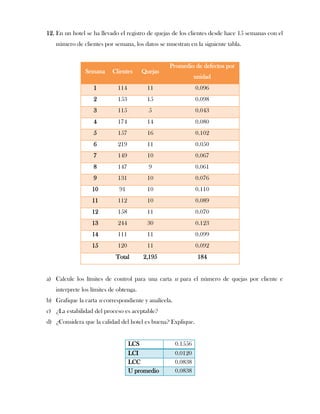
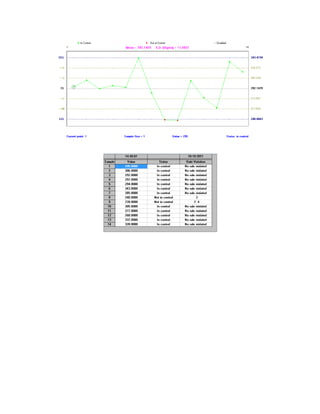
Este documento presenta tres ejercicios prácticos sobre análisis de Pareto aplicado a problemas de calidad en diferentes empresas. El primer ejercicio identifica quejas de clientes, encontrando que el tipo D causa la mayor insatisfacción. El segundo analiza defectos en envasado de tequila, concluyendo que etiquetas y botellas sin vigusa son los principales problemas. El tercer ejercicio identifica problemas en salchichas, determinando que la falta de vacío es el defecto vital, siendo el turno II la principal causa.

1. Universidad Católica de
UNICAH Honduras
“Nuestra Señora Reina de la Paz”
Campus San Isidro
Guía de Ejercicios Prácticos
Asignatura:
Aplicación de la Calidad Total para
la Ingeniería Industrial
Catedrático:
Ing. Jairo Núñez
Alumno:
Erick Joel Ocampo
0201198500735
La Ceiba, Atlántida, Honduras, C.A.
10 de octubre de 2011

2. GUÍA DE EJERCICIOS
1. En una empresa, mediante un análisis se ha detectado que se tiene seis tipos básicos de
quejas de los clientes, pero cada tipo de queja causó diferente grado de insatisfacción o
molestia para el cliente. La escala que se ha utilizado para medir el grado de molestia es el
siguiente: máxima molestia (10 puntos), mucha insatisfacción (8), molestia moderada (6),
poca (4), muy leve (2). Además en el análisis se determinó la frecuencia con la que han
ocurrido en el último semestre las distintas quejas. En las tablas siguientes se sintetiza los
resultados de tal análisis:
Tipo de queja Grado de molestia Frecuencia de ocurrencia
A 4 12%
B 8 5%
C 2 40%
D 6 25%
E 4 10%
F 8 8%
Realice un análisis de Pareto para determinar sobre qué tipo de queja se deben dirigir los esfuerzos
para atender sus causas. Aplique la recomendación 2 del diagrama de Pareto.
Frecuencia de Frecuencia por Frecuencia por
Tipo de queja Grado de molestia
ocurrencia gravedad gravedad acumulada
D 6 25% 150% 150%
C 2 40% 80% 230%
F 8 8% 64% 294%
A 4 12% 48% 342%
E 4 10% 40% 382%
B 8 5% 40% 422%

3. Diagrama de Pareto
160% 450%
140% 400%
120% 350%
300%
100%
Frecuencia
250%
80%
200% Frecuencia
60% % acumulado
150%
40% 100%
20% 50%
0% 0%
D C F A E B
Clase

4. Análisis
Para poder realizar este análisis de Pareto y determinar así la queja que más contribuye a la
insatisfacción de los clientes se multiplicó el grado de la queja por la frecuencia de ocurrencia. Con
ellos vemos que la queja D supera a las demás en magnitud, por lo tanto es en esta que se debe de
poner el mayor atención ejecutar acciones destinadas a reducir las causantes del descontento de los
clientes y de ser posible eliminar tal tipo de insatisfacción.
2. De acuerdo con la información de una hoja de verificación en una línea del proceso de
envasado de tequila, se presentaron en el último mes los siguientes resultados en cuanto a
defectos y frecuencia:
Defecto de envasado Frecuencia
Botella 804
Tapa 715
Etiqueta 1,823
Contraetiqueta 742
Botella sin vigusa 916
Otros 102
Total de botellas envasadas en el mes 424,654
Realice un diagrama de Pareto y obtenga conclusiones.
Defecto de envasado Frecuencia % Frecuencia F. Acumulada
Etiqueta 1,823 36% 36%
Botella sin vigusa 916 18% 54%
Botella 804 16% 69%
Contraetiqueta 742 15% 84%
Tapa 715 14% 98%
Otros 102 2% 100%
Total de botellas
envasadas en el mes 5,102 100%

5. Histograma
2,000 120%
1,800
1,600 100%
1,400 80%
Frecuencia
1,200
1,000 60%
800
600 40%
400 Frecuencia
20%
200 % acumulado
0 0%
Clase

6. Análisis
De acuerdo al análisis estadístico realizado se puede apreciar claramente que los defectos de
etiqueta, botella sin vigusa, en la botella y en la contraetiqueta componen el 84% de los problemas
que se presentan en el proceso de envasado del tequila. De los cuales, componen el 36% y 18% los
defectos en las etiquetas y la botella sin vigusa. Debido a esto la empresa deberá fijar toda su
atención para poder encontrar las causas que los generan para poder garantizar la calidad y poder
proporcionar mayor satisfacción a sus clientes.
3. En una empresa procesadora de carnes frías se detecta mediante inspección 100% los
problemas en las salchichas. A continuación se muestran los resultados de una semana.
Máquina Problema y número de paquetes defectuosos
Turno
empacadora Falta de vacío Mancha verde Mancha amarilla
A I 4,300 700 700
II 6,300 650 650
B I 3,500 700 400
II 6,600 500 420
C I 8,500 800 324
II 9,120 655 345
a) Considerando que la gravedad de los tres problemas es la misma, realice un análisis de
Pareto para problemas y detecte cuál es el vital.
b) Sobre el problema vital, haga un Pareto de segundo nivel (causas) tanto para máquina
como para turno.

7. Pareto I Nivel (Problemas)
Problema Frecuencia % Frecuencia F. Acumulada
Falta de Vacío 38,320 85% 85%
Mancha verde 4,005 9% 94%
Mancha amarilla 2,839 6% 100%
Total 45,164
Análisis de Pareto para Problemas
45,000 105%
40,000
100%
35,000
30,000 95%
Frecuencia
25,000
90%
20,000
15,000 85% Frecuencia
10,000 % acumulado
80%
5,000
0 75%
Falta de Vacío Mancha verde Mancha
amarilla
Clase

8. Pareto II Nivel (Turnos)
Falta de vacío Frecuencia % Frecuencia F. Acumulada
Turno II 22,020 57% 57%
Turno I 16,300 43% 100%
Total 38,320 100%
Análisis de Pareto para Turnos
25,000 120%
20,000 100%
80%
Frecuencia
15,000
60%
10,000 Frecuencia
40%
% acumulado
5,000 20%
0 0%
Turno II Turno I
Clase

9. Pareto II Nivel (Máquinas)
Máquina Frecuencia % Frecuencia F. Acumulada
C 17,620 46% 46%
A 10,600 28% 74%
B 10,100 26% 100%
Total 38,320 100%
Análisis de Pareto para Máquinas
20,000 120%
100%
15,000
80%
Frecuencia
10,000 60%
Frecuencia
40%
5,000 % acumulado
20%
0 0%
C A B
Clase

10. Análisis
 En el primer análisis de Pareto se observa de forma clara que el 85% de los problemas
relacionados al procesado de las salchichas se deben a la falta de vacío, por lo que este es
identificado como el problema vital más relevante, en consecuencia se desarrollará por lo
tanto un Pareto de segundo nivel tanto en las máquinas como en los turnos para identificar
en cuál de ellos se presentan mayores fallas.
 En el diagrama de Pareto que considera los turnos se puede apreciar que la cantidad de
problemas relacionados con la falta de vacío en el procesamiento de las salchichas es mayor
durante el turno 2, ya que éste constituye el 57% del total de los problemas de este tipo.
Con esto se concluye, a través del análisis de Pareto, que los problemas de falta de vacío se
dan con mayor frecuencia en la máquina C, durante el turno 2.
 Con base en el Pareto de 2do. Nivel se puede observar que las máquinas C y A son las
principales causas de la falta de vacío; siendo la causa más significante la maquina C ya que
representa el 46% de los problemas relacionados con la falta de vacío que es el principal
problema con el que cuenta el proceso y el que necesita de una pronta solución.
4. En una fábrica de pintura se requiere reducir el tiempo de secado del barniz, los siguientes
datos corresponden al tiempo del secado del barniz (horas) y a la cantidad de aditivo con el
que se intenta lograr tal reducción.
Cantidad de Tiempo de
Aditivo Secado
0 14
1 11
2 10
3 8
4 7.5
5 9
6 10
7 11
8 13
9 12
10 15
a) Mediante un diagrama de dispersión investigue la relación entre el tiempo de secado y la
cantidad de aditivo.

11. b) Con base en la relación, ¿alrededor de qué cantidad de aditivo recomendaría para reducir
el tiempo de secado?
c) Obtenga el coeficiente de relación entre ambas variables e interprételo.
d) Al parecer el coeficiente de correlación lineal es muy bajo. ¿Quiere decir entonces que el
tiempo de secado no está relacionado con la cantidad de aditivo?
Relación Aditivo - Tiempo de Secado
y = 0.2409x + 9.75
16
R² = 0.1116
14
12
Tiempo de Secado
10
8
Tiempo de Secado
6
Lineal (Tiempo de Secado)
4
2
0
0 2 4 6 8 10 12
Cantidad de Aditivo
Análisis
a) Como se observa en la gráfica la cantidad de aditivo y el tiempo de secado tienen una
relación lineal positiva baja, lo que indica que son directamente proporcionales, es decir, a
mayor cantidad de aditivo se necesitarán más horas de secado.
b) Basado en la relación, recomendaría el 4 de aditivo para reducir el tiempo de secado, pues
según la gráfica, es el que registra menor tiempo de secado, es decir, 7.5 horas.
c) El coeficiente de relación es de 0.33 este valor muestra que existe una relación positiva baja
entre la cantidad de aditivo y el tiempo de secado.
d) En efecto si existe relación pero es una relación baja ya que el coeficiente de correlación es
un tanto leve.
5. En una industria se desea investigar cómo influye la temperatura (°C) en la presión del
vapor B-trimetilboro. Los datos obtenidos para tal propósito se muestran a continuación:

12. Temperatura Presión
13.0 2.9
19.5 5.1
45.7 30.5
56.1 51.4
64.4 74.5
71.4 100.2
80.5 143.7
85.7 176.9
22.5 8.5
27.2 10.3
31.8 14.6
a) Construya un diagrama de dispersión e interprételo.
b) Obtenga el coeficiente de correlación y al interpretarlo compare con lo observado en el
inciso a.
Relación Temperatura - Presión
200
150 y = 2.213x - 47.935
R² = 0.8981
Presión
100
Lineal (Presión)
Presión Lineal (Presión)
50 Lineal (Presión)
0
0.0 20.0 40.0 60.0 80.0 100.0
-50
Temperatura

13. Análisis
Existe una relación lineal positiva entre la presión y la temperatura, aunque se asemeja más a una
relación del tipo exponencial. El coeficiente de correlación es de R=0.95 lo que muestra que existe
una alta relación entre las variables estudiadas, con lo que podemos afirmar que la temperatura
incide de manera importante sobre la presión, es decir, a mayor temperatura, mayor presión.
6. Como parte del análisis del problema de ausentismo se decide investigar la relación entre
edad del empleado y días que faltó a laborar en el año. Los datos del último año se
muestran a continuación.
Empleado Edad Faltas Empleado Edad Faltas
1 29 6 21 25 7
2 33 5 22 38 3
3 40 0 23 22 0
4 23 8 24 30 4
5 31 6 25 24 7
6 20 9 26 39 10
7 30 5 27 35 5
8 38 5 28 20 1
9 23 8 29 32 5
10 25 6 30 25 5
11 26 7 31 36 5
12 30 5 32 30 5
13 42 2 33 20 10
14 34 5 34 38 4
15 31 6 35 39 4
16 18 11 36 34 4
17 33 6 37 35 6
18 33 4 38 27 7
19 33 5 39 40 3
20 32 5 40 31 6
a) Mediante un diagrama de dispersión analice la relación entre estas dos variables.
b) ¿Qué tipo de relación observa y cuáles son algunos hechos especiales?
c) Calcule el coeficiente de correlación e interprételo.

14. Relación Edad - Faltas
12
10 y = -0.1665x + 10.47
R² = 0.1958
8
Días Faltados
6
Faltas
4 Lineal (Faltas)
2
0
0 10 20 30 40 50
Edad del Trabajador
Análisis
Se puede observar que existe una relación lineal negativa entre las variables que son objeto de
nuestro estudio, la edad y el número de días que los empleados faltan a sus trabajos; esto sugiere
que entre más joven es el empleado esta más susceptible al ausentismo. Al calcular el coeficiente
de correlación el cual es de R= 0.44 se tiene una mayor certeza que entre las variables existe una
relación lineal negativa media.
7. Dos máquinas, cada una operada por una persona, son utilizadas para cortar tiras de hule,
cuya longitud ideal es de 200mm, con una tolerancia de ± 3 mm. Al final del turno un
inspector toma una muestra e inspecciona que la longitud cumplía especificaciones. A
continuación se muestran las últimas 110 mediciones para ambas máquinas.
Muestras (mm)
199.2 201.7 200.9 201.0 200.6 199.5 199.0 199.2 199.0 198.9
199.7 201.4 200.7 201.4 200.1 198.6 198.4 198.8 199.0 199.2
201.8 201.4 200.5 201.4 201.3 200.3 199.1 198.5 198.7 197.9
202.0 200.8 201.2 201.1 200.6 198.5 198.8 198.9 199.1 200.3
201.0 202.1 201.7 201.2 200.7 198.2 198.3 198.8 200.3 199.6
201.5 200.7 201.2 201.0 201.8 199.6 198.9 198.7 200.5 199.4
200.0 200.9 201.2 200.6 200.5 198.2 199.6 199.2 198.1 198.7
199.8 201.0 200.5 202.0 200.5 198.4 199.0 199.3 198.3 198.5
200.7 201.5 200.1 201.0 200.8 199.0 198.7 199.7 199.6 198.7

15. 201.4 201.2 201.4 201.5 200.3 199.7 200.5 197.8 199.0 198.6
200.4 201.3 200.2 201.6 200.7 199.7 198.4 199.9 199.7 198.5
a) Obtenga las medidas de tendencia central y con base en ellas señale si la tendencia central
del proceso es adecuada.
b) Calcule la desviación estándar y una aproximación de los límites reales con base en estos
decida si la variabilidad de los datos es aceptable.
c) Obtenga un histograma e interprételo (con tendencia Central, variabilidad, acantilados,
sesgos, etc.).
Histograma
30
25
Frecuencia
20
15
10
5
0
Milímetros

16. Media 200.05 LRS 203.91
Error típico 0.12 LRI 196.18
Mediana 200.1
Moda 199
Desviación estándar 1.29
Varianza de la muestra 1.66
Curtosis 2.53
Coeficiente de asimetría 0.80
Rango 8.20
Mínimo 197.80
Máximo 206
Suma 22005
Cuenta 110
Análisis
Tomando las 110 muestras, se obtuvo una media de 200.05 mm, una mediana o percentil 50 de
200.10 mm que nos dice que la mitad de los datos son menores que 200.10 mm y la otra mitad
mayores o iguales a 200.10 mm, y una moda de 201.4. Además se obtuvo un error típico de 0.12;
La desviación estándar de 1.29 lo que nos indica que el grado de dispersión de los datos respecto
a su media. El coeficiente de asimetría de 0.80 indica que existe una curva asimétrica positiva. El
coeficiente de Curtosis es de 2.53, nos demuestra que la grafica posee una forma leptocúrtica, es
decir que presenta un elevado grado de concentración de valores a la derecha de la media que a su
izquierda. Podemos notar también que la forma de la gráfica obedece a una Histograma centrado
con mucha variabilidad. El Rango de los datos es de 8.2 mm, ya que el menor es 197.8 mm y el
mayor es 206 mm, por lo tanto extensión de la variación de los datos no es tan grande. Podemos
afirmar que el histograma no presenta acantilados en su gráfica, pero si posee sesgo a la izquierda
de la media, lo que podemos constatar observando la barra de color verde el cual es la clase con
mayor numero de datos asociados. Los límites reales se definan por:
8. En un área de servicio dentro de una empresa de manufactura se hace una encuesta para
evaluar la calidad del servicio proporcionada y el nivel de satisfacción de los clientes
internos. La encuesta consiste de 10 preguntas, donde cada una de ellas evalúa diferentes
aspectos del servicio proporcionado. Las respuestas para cada pregunta es un número entre
0 y 10. Para hacer un primer análisis de los resultados obtenidos, se suman los puntos

17. obtenidos de las 10 preguntas para cada cuestionario. A continuación se muestran los
puntos obtenidos en 50 cuestionarios.
Muestras
78 78 82 85 81 86 80 73 84 78
68 84 75 78 76 76 82 85 91 80
70 87 77 82 84 48 49 39 39 43
35 42 34 44 49 34 30 43 31 34
41 42 45 42 35 38 39 42 43 29
a) A los datos anteriores calcúleles sus medias de tendencia central, su dispersión y de una
primera opinión sobre la calidad del servicio.
b) Realice el histograma e interprételo con cuidado.
Media 59.8
Error típico 2.99
Mediana 58.5
Moda 42
Desviación estándar 21.13
Varianza de la muestra 446.29
Curtosis -1.80
Coeficiente de asimetría -0.02
Rango 62
Mínimo 29
Máximo 91
Suma 2990
Cuenta 50
Histograma
15
Frecuencia
10
5
0
29 37.86 46.71 55.57 64.43 73.29 82.14 y
mayor...
Calificación

18. Análisis
Los datos estadísticos obtenidos a través de la encuesta, proporcionaron los siguientes resultados:
una media de 59.8 puntos, la mediana o percentil 50 es de 58.5 puntos y una moda de 42 puntos.
Un error típico de 2.99; la desviación estándar de los datos con respecto a su media es de 21.13
puntos un valor demasiado elevado por lo que podemos afirmar que los datos se encuentran muy
dispersos con respecto a su media, es decir que existe mucha variabilidad. Con una Curtosis de -
1.80, nos expone que la campana de Gauss posee una forma plana, es decir, una forma achatada.
La curva asimétrica es negativa esto se puede observar a través del valor del coeficiente de asimetría
que es de -0.02. Con una puntuación mínima de 29 y máxima de 91, nos indica que existe una
gran variabilidad en los datos ya que posee un rango de 62 puntos el cual mide la gran amplitud en
la variación de los datos. La forma del histograma supone una descentralización con mucha
variabilidad y dos realidades, es decir que es bimodal.
9. En la elaboración de envases de plásticos, primero se elabora la preforma, para la cual se
tienen varios criterios de calidad, uno de ellos es ep peso de la preforma. Para cierto
envase se tiene que el peso debe estar entre 28.00 ± 0.5g. A continuación se muestran los
últimos 112 datos obtenidos mediante una carta de control para esta variable.
Muestras
27.72 28.39 28.21 28.19 28.02 27.92 27.89 27.88
28.06 27.91 27.91 27.95 27.96 27.94 28.04 28.05

19. 27.81 27.74 27.95 27.91 27.93 28.07 28.13 27.93
27.87 27.87 27.82 28.23 27.90 27.91 28.16 27.94
27.86 27.84 27.70 27.98 28.02 28.00 27.99 28.13
28.26 28.10 27.94 28.07 27.84 27.90 27.87 27.76
27.95 27.94 27.81 27.76 27.96 27.84 27.85 27.93
28.22 27.96 27.88 28.08 28.04 28.19 27.89 28.08
28.09 28.02 27.85 28.27 27.75 27.98 27.75 27.82
28.13 27.88 28.11 28.05 28.14 28.11 28.08 28.16
28.04 28.05 27.75 27.89 27.94 28.19 28.10 27.78
27.63 27.93 27.74 28.10 28.14 27.91 27.84 28.21
27.85 27.84 28.12 28.01 27.97 27.88 28.00 28.10
28.16 28.16 28.01 28.13 27.97 27.90 27.87 27.94
a) Obtenga las medidas de tendencia central y señale si la tendencia central de las mediciones
es adecuada.
b) Calcule la desviación estándar y una aproximación de los límites reales y con base en estos
decida si la variabilidad de los datos es aceptable.
c) Obtenga un histograma e interprételo (tendencia central, variabilidad, acantilados, sesgos,
etc.).
Media 27.97
Error típico 0.01
Mediana 27.95
Moda 27.94
Desviación estándar 0.14
Varianza de la muestra 0.02
Curtosis -0.30
Coeficiente de 0.21
asimetría
Rango 0.76
Mínimo 27.63
Máximo 28.39
Suma 3133.19
Cuenta 112

20. Histograma
30
25
20
Frecuencia 15
10
5
0
Gramos
Análisis
Con relación a los datos de las 112 muestras se obtuvieron los siguientes resultados una media de
27.97, una mediana de 27.95, la moda es de 27.94. Un error típico de 0.01; la desviación estándar
es de 0.14, lo que indica que hay poca dispersión en el peso de los envases con respecto a la media
de los datos. La Curtosis es -0.26, lo que indica que el curva de Gauss tiene una forma platicúrtica,
es decir, que la grafica es de forma achatada. El rango es de 0.76, puesto que el peso menor es
27.63 y el máximo de 28.39. Por lo tanto la amplitud de la variación de los datos es un tanto

21. aceptable. La grafica posee un coeficiente de asimetría que muestra que es una curva asimétrica
positiva. En cuanto a la forma del histograma podemos aseverar que éste está centrado con mucha
variabilidad. No hay acantilados y no hay evidencia de sesgo ni datos aislados.
10. Los siguientes datos corresponden a la medición de la viscosidad, variable importante en la
calidad del adhesivo.
a) Calcule los límites de control para las cartas X-R e interprételos
b) Elabore la carta de control X y la R y de sus conclusiones.
Semana 29 Semana 30 Semana 31
H H H H H H H H H
1 2 3 4 5 6 7 8 9
I I I II II II I I I
17-jul 18-jul 19-jul 19-jul 25-jul 26-jul 31-jul 01-ago 02-ago
1 34.0 33.0 34.0 35.0 34.0 35.0 33.0 34.0 35.0
2 34.0 33.0 34.0 35.0 34.0 35.0 33.0 34.0 35.0
3 34.0 34.0 34.0 34.0 34.0 34.0 34.0 35.0 35.0
4 35.0 34.0 34.0 34.0 35.0 34.0 34.0 35.0 34.0
5 35.0 35.0 35.0 34.0 35.0 33.0 34.0 35.0 34.0
6 35.0 35.0 35.0 34.0 35.0 33.0 34.0 34.0 34.0
7 35.0 35.0 35.0 35.0 35.0 34.0 35.0 34.0 35.0
8 34.0 34.0 34.0 35.0 34.0 35.0 35.0 35.0 35.0
9 34.0 34.0 34.0 35.0 34.0 35.0 35.0 35.0 35.0
Carta X
35.0
34.8
34.6
Promedio
34.4
LCS
34.2
LCC
34.0
LCI
33.8
33.6
33.4
1 2 3 4 5 6 7 8 9 10

22. LCS 34.8
LCC 34.4
LCI 33.9
A2 0.337
Análisis: El proceso de viscosidad en los adhesivos esta dentro de control estadístico en cuanto a
su medida de tendencia central, con un LIC= 33.90 y un LCS= 34.80. Todos los datos
muestreados están dentro de los límites de control establecidos para esta carta.
Carta R
3
2.5
2
Rango
1.5 LCS
LCC
1 LCI
0.5
0
1 2 3 4 5 6 7 8 9 10

23. D3 0.1838
D4 1.8162
LCS 2.4
LCC 1.3
LCI 0.2
Análisis: El proceso de viscosidad en los adhesivos esta dentro de control estadístico en cuanto a la
variabilidad de los datos, es decir en cuanto a sus rangos, ningún valor excede los límites de control
respectivos. El rango de la viscosidad de dichos adhesivos se encuentra entre 0.25 y 2.42 con un
rango promedio de 1.3. Lo cual indica que existe poca variabilidad en la viscosidad del adhesivo.
11. En una industria alimenticia se quiere garantizar que la concentración mínima de grasa de
un producto sea de 1.8%. En la siguiente tabla, se muestran los datos obtenidos para el
estudio inicial, con tamaño de subgrupo de 4.
GRASA GRASA
SUB SUB
GRUPO GRUPO
1 2 3 4 1 2 3 4
1 1.88 1.93 1.98 1.88 11 1.93 1.95 1.90 1.93
2 1.93 1.97 1.89 1.94 12 1.95 1.98 1.89 1.90

24. 3 1.92 1.95 1.90 1.98 13 1.88 1.93 1.88 1.90
4 1.89 1.89 1.90 1.94 14 1.97 1.88 1.92 1.96
5 1.95 1.95 1.93 1.90 15 1.91 1.91 1.96 1.93
6 2.00 1.95 1.94 1.89 16 1.98 1.90 1.92 1.91
7 1.95 1.93 1.97 1.85 17 1.93 1.94 1.95 1.90
8 2.87 1.98 1.96 2.04 18 1.82 1.92 1.95 1.94
9 1.96 1.92 1.98 1.88 19 2.00 1.97 1.99 1.95
10 1.99 1.93 2.01 2.02 20 1.98 1.94 1.96 1.88
a) Calcule los límites de control para las cartas X-R e interprételos.
b) Elabore la carta de control X y la R y de sus conclusiones.
Carta X
n 4
A2 0.729
X 1.946
LCS 2.035
LCI 1.858
LCC 1.946
R 0.122
2.300
2.200
2.100
2.000 Promedio
LCS
1.900 LCI
LCC
1.800
1.700
1.600
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

25. Análisis: El proceso de concentración de grasa en el producto se encuentra fuera de control
estadístico en cuanto a su medida de tendencia central ya que la muestra 8 está por arriba del límite
de control superior, el punto 9 viola la regla 14 la cual dice que este punto está por debajo de 4
sigmas. Y la muestra 18 viola la prueba 8 que indica que hay 8 puntos consecutivos en la zona C (1
sigma). La concentración de grasa en los productos se encuentra entre 1.86 y 2 con un promedio
de 1.95.

26. Carta R
LCS 0.28
LCC 0.12
LCI 0
D3 0
D4 2.28
1.000
0.900
0.800
0.700
0.600 Rango
0.500 LCS
0.400 LCC
0.300 LCI
0.200
0.100
0.000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

27. Análisis: El proceso de concentración de grasa en los productos se encuentra fuera de control
estadístico en cuanto a su medida dispersión o variabilidad ya que la muestra 8 está por arriba del
límite de control superior. El rango de la concentración de grasa en los productos se encuentra
entre 0.0% y 0.28% con un rango promedio de 0.1 %. Lo cual indica que existe poca dispersión en
la viscosidad del adhesivo.
12. En la fábrica de discos ópticos una máquina metaliza disco. Para garantizar la uniformidad
del metal en el disco, la densidad debe ser de 1.93, con una tolerancia de ±0.12, en la tabla
siguiente se muestran los datos obtenidos para un estudio inicial, con tamaño de subgrupo
5.
SUB
GRUPO
DATOS
1 1.909 1.917 1.865 1.991 1.906
2 1.957 1.829 1.87 1.917 1.971
3 1.861 1.946 1.903 1.951 1.893
4 1.938 1.913 1.884 1.907 1.95
5 1.941 1.966 1.935 1.936 1.955
6 2.032 1.914 1.911 1.82 1.932
7 1.889 1.963 1.943 1.918 1.911
8 1.891 1.978 1.907 1.922 1.908
9 1.929 1.87 1.943 1.819 1.946
10 1.956 1.904 1.904 1.907 1.864
11 1.904 1.91 1.904 1.903 1.901
12 1.926 1.984 1.899 1.938 1.978
13 1.936 1.903 1.915 1.932 2.014
14 1.937 1.949 1.898 1.952 1.869
15 1.916 1.961 1.953 1.954 1.939
16 1.867 1.898 1.929 1.953 1.952
17 1.939 1.918 1.925 1.949 1.91

28. 18 1.94 1.88 1.882 1.949 1.91
19 1.944 1.919 1.84 1.94 1.942
20 1.933 1.965 2.031 1.902 1.923
21 1.817 1.878 1.938 2.058 1.938
22 1.939 1.956 1.951 1.898 1.969
23 1.931 1.894 1.972 1.936 1.924
24 1.927 1.895 1.938 1.859 1.938
25 1.973 1.949 1.912 1.87 1.971
a) Calcule los límites de control para las cartas X-R e interprételos.
b) Elabore la carta de control X y la R y de sus conclusiones.
Carta X
n 5
A2 0.577
X 1.924
LCS 1.979
LCI 1.869
LCC 1.924
R 0.095
2.000
1.980
1.960
1.940
1.920 Promedio
1.900 LCS
1.880 LCI
LCC
1.860
1.840
1.820
1.800
1 3 5 7 9 11 13 15 17 19 21 23 25

29. Análisis: Con base en el análisis de los datos mediante una carta X el proceso de fabricación discos
ópticos la densidad se encuentra bajo control estadístico en cuanto a su medida de tendencia
central ya que todos los datos están dentro de los límites de control superior e inferior. La
densidad en el metal para los discos se encuentra entre 1.924 y 1.979 con un promedio de 1.869.
En conclusión el proceso está bajo control estadístico.

30. Carta R
0.300
0.250
0.200 Rango
0.150 LCS
LCC
0.100
LCI
0.050
0.000
1 3 5 7 9 11 13 15 17 19 21 23 25

31. Análisis: Basado en la Carta de Rangos el proceso de fabricar discos ópticos la densidad está fuera
de control estadístico en cuanto a su variabilidad ya que los puntos 6 y 21 se encuentran por
encima del límite de control superior. El rango de la densidad en el metal para fabricar los discos
ópticos se encuentra entre 0.00 y 0.200 con un rango promedio de 0.095.
13. En la presentación de servicios en una empresa se registra diariamente la evaluación de los
clientes. La forma operativa que se hace es la siguiente: todos los días en forma aleatoria se
le pide a 5 clientes atendidos que contesten una encuesta de satisfacción en el servicio, la
escala de satisfacción va de 0 a 100. Los datos obtenidos durante el último mes se
muestran en la tabla siguiente.
a) Mediante una carta de medias analice la estabilidad de la calidad en el servicio.
DÍA CALIFICACIÓN DE SERVICIOS MEDIA
1 83 84 63 68 93 78.20
2 84 88 71 87 93 84.60
3 87 76 92 75 79 81.80
4 71 69 79 79 62 72.00
5 76 81 100 85 100 88.40
6 69 86 98 84 89 85.20
7 88 89 75 72 86 82.00
8 96 76 71 97 73 82.60
9 61 71 57 90 79 71.60
10 82 93 87 87 76 85.00
11 80 82 66 83 83 78.80
12 69 84 89 88 65 79.00
13 50 92 76 62 71 70.20
14 74 94 73 79 67 77.40
15 66 74 86 78 72 75.20
16 80 82 84 60 83 77.80
17 57 87 74 94 72 76.80
18 99 88 83 90 80 88.00
19 87 80 89 89 77 84.40
20 79 85 65 71 70 74.00
21 93 70 77 80 74 78.80
22 73 76 81 80 65 75.00

32. n 5
LCS 131.67
LCC 79.40
LCI 27.13
A2 0.58
R promedio 90.59
Carta X
140.00
120.00
100.00
Media
80.00
LCS
60.00 LCC
LCI
40.00
20.00
0.00
1 3 5 7 9 11 13 15 17 19 21

33. Análisis: Según la carta de medida de tendencia central, la calidad del servicio se encuentra en
control estadístico, ya que todas las observaciones caen dentro de los límites de control para dicha
carta. La satisfacción de los clientes se encuentra entre 131.67 y 27.13 con una satisfacción
promedio de 79.4.
Carta R
D3 0
D4 2.11
LCS 191.55
LCC 90.59
LCI 0
250.00
200.00
150.00 Rango
LCS
100.00 LCC
LCI
50.00
0.00
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

34. Análisis: Basados en la Carta R, la calidad del servicio se encuentra bajo control estadístico, en
cuanto a la variabilidad de los datos se refiere ya que todas las observaciones no violan los límites
de control. El rango de satisfacción en los clientes se encuentra entre 0.0 y 191.55 con una
satisfacción promedio de 90.59. Por tanto podemos concluir que tal proceso funciona de una
forma estable.

35. CAPÍTULO 2
1. Con los datos del ejercicio de las dos máquinas operadas por una persona, considerando
que los primeros 55 datos (ordenados por reglón) corresponden a una máquina, y los
últimos 55 a otra, conteste lo siguiente.
a) Evalúe las dos máquinas en cuanto a su centrado (tendencia central) respecto a la
longitud ideal (200).
b) Analice la dispersión de ambas máquinas, utilizando la desviación estándar.
c) Haga un histograma para cada máquina e interprete cada uno de ellos.
d) Con base en lo anterior, ¿cuál es el problema de cada máquina?
e) Considerando que cada máquina es operada por una persona diferente, discuta cuáles
son las posibles causas de los problemas señalados en el inciso anterior y señale qué
haría para corroborar cuáles son las verdaderas causas.
f) Vuelva a analizar el histograma realizado en el inciso c del ejercicio anterior y vea si de
alguna forma se vislumbraba lo que detectó con los análisis hechos en este ejercicio.
g) A la luz de lo anterior, ¿qué recomendaciones respecto a la obtención de datos y su
análisis daría para hacer más eficiente la inspección y el control del funcionamiento de
cada máquina?
Máquina 1
Media 200.13
Error típico 0.17
Mediana 200.3
Moda 201.4
Desviación estándar 1.23
Varianza de la muestra 1.50
Curtosis -1.39
Coeficiente de asimetría -0.09
Rango 4.2
Mínimo 197.9
Máximo 202.1
Suma 11007.1
Cuenta 55

36. Histograma "Máquina 1"
14
12
10
Frecuencia
8
6
4
2
0
Milímetros
Análisis: Basados en la información y gráficos obtenidos se ve claramente de que en la máquina 1
los datos se encuentran poco dispersos con respecto a la media (dispersión), pero sin embargo, la
empresa debe de reducirla. La mediana o percentil 50 nos indica que la mitad de los datos tienen
un valor por debajo de 200.3 mm, y la otra parte, su valor es mayor o igual a 200.3 mm. La curtosis
es de -1.39 lo que indica que la curva de la distribución normal presenta un grado reducido de
concentración alrededor de los valores centrales de la variable estudiada, es decir que presenta una
forma aplanada o achatada. El coeficiente de asimetría es 0 por lo que se concluye que existe una
mayor concentración de valores a la izquierda de la media que a su derecha. Aquí se aprecia que se
presentan dos realidades distintas (bimodal) lo que indica que hay situaciones que causan esto y
deben ser identificadas para erradicarlas.

37. Máquina 2
Media 199.97
Error típico 0.18
Mediana 199.8
Moda 200.5
Desviación estándar 1.37
Varianza de la muestra 1.87
Curtosis 5.52
Coeficiente de asimetría 1.50
Rango 8.2
Mínimo 197.8
Máximo 206
Suma 10998.4
Cuenta 55
Histograma "Máquina 2"
18
16
14
Frecuencia
12
10
8
6
4
2
0
Milímetros

38. Análisis: Basados en la información y gráficos obtenidos se puede ver que en la máquina 2 los
datos se encuentran poco dispersos con respecto a la media (dispersión), pero sin embargo es
mayor que el de la máquina 1 y la empresa debe de reducirla. La mediana o percentil 50 nos
indica que la mitad de los datos tienen un valor por debajo de 199.8 mm, y la otra parte, su valor es
mayor o igual a 199.8 mm. La curtosis es de 5.52 lo que indica que la curva de la distribución
normal presenta un elevado grado de concentración alrededor de los valores centrales de la
variable estudiada, es decir que presenta una forma alargada en el centro. El coeficiente de
asimetría es >0 por lo que se concluye que existe una mayor concentración de valores a la derecha
de la media que a su izquierda. Con respecto a la máquina 1, la 2 presenta un mejor estado porque
en esta claramente solo hay una realidad por lo tanto es más fácil poder controlarlo y erradicarlo.
2. Con el propósito de mejorar la calidad que se tenía en cuanto al grosor de las láminas, un
grupo implementa un proyecto de mejora siguiendo la metodología. Varios de los cambios
implementados fueron relativos a los procedimientos empleados durante el proceso ya y la
estandarización de los mismos. Para verificar si el plan tuvo éxito, se eligieron láminas
aleatoriamente y midiendo su grosor. Los 120 datos obtenidos durante tres días se
muestran a continuación.
4.8 4.3 4.8 5.1 4.9 4.6 4.9 4.6 5.0 4.9 4.8 4.5
4.7 5.7 4.5 5.3 4.4 5.1 4.6 4.9 4.2 4.6 5.3 5.2
4.7 4.1 5.1 5.0 5.0 4.9 4.6 4.9 5.2 4.8 4.7 5.1
4.9 4.8 4.7 5.1 5.1 5.3 5.1 5.0 5.3 5.0 5.1 5.2

39. 4.7 5.0 5.0 5.3 5.1 5.1 4.5 5.2 4.1 5.1 4.9 4.9
4.6 5.0 4.6 4.8 4.7 4.9 4.4 4.5 5.3 5.3 4.4 5.0
4.2 4.5 5.3 5.1 4.8 4.4 4.7 5.3 5.1 4.7 4.7 4.8
5.0 5.0 4.9 5.2 5.6 5.1 5.2 4.5 4.6 5.2 4.9 5.0
5.3 4.9 5.0 4.4 4.9 4.7 4.6 5.3 4.8 4.7 4.6 5.1
4.4 5.0 4.5 5.0 5.2 4.7 5.0 5.3 5.6 5.0 5.0 4.5
a) Calcule la media y mediana de estos datos, y comparándolas con sus correspondientes
antes del proyecto, decida si con los cambios se mejoró el centrado del proceso.
μ= 4.75, mediana= 4.7
b) Calcule la desviación estándar, y con ésta, obtenga los nuevos límites reales, y decida si la
variabilidad se redujo. σ= 0.45
c) Construya un histograma.
d) Con base en todo lo anterior, ¿el proyecto dio buenos resultados? Argumente.
e) Si hubo mejoras, ¿éstas son suficientes para garantizar un producto dentro de
especificaciones?
Datos del Estudio Anterior
Desviación estándar 0.45 mm
Grosor óptimo 5 mm
Discrepancia 0.8 mm
Mediana 4.7 mm
Media 4.75 mm
LRS 6.1 mm
LRI 3.4 mm
Datos del Estudio Actual
Media 4.88
Error típico 0.03
Mediana 4.9
Moda 5
Desviación estándar 0.32
Varianza de la muestra 0.10
Curtosis -0.12

40. Coeficiente de asimetría -0.18
Rango 1.6
Mínimo 4.1
Máximo 5.7
Suma 586.1
Cuenta 120
Histograma
25
20
Frecuencia
15
10
5
0
Milímetros

41. LRS 5.83 mm
LRI 3.94 mm
Análisis: Se puede ver claramente que los datos, en cuanto a su dispersión con respecto a la media
se redujo, la desviación estándar paso de 0.45 0 0.32 aproximándose más a cero, que es lo ideal. El
índice de Curtosis nos dice que la curva de la normal tiende a ser achatada con colas cortas y el
coeficiente de asimetría nos dice que existe mayor concentración de datos a la izquierda que a la
derecha. Con ello se puede afirmar que se ha logrado una mejora pero se debe seguir mejorando
ya que, aunque el proceso está centrado presenta variabilidad.
3. Una característica clave en la calidad de las pinturas es su densidad y un componente que
influye en tal densidad es la cantidad de arenas que se utilizan en su elaboración. La
cantidad de arena en la formulación de un lote se controla con base en el número de
costales, que según el proveedor contienen 20 kg. Sin embargo, continuamente se tienen
problemas en la densidad de la pintura, que es necesario corregir con retrabajo y
reprocesos adicionales. En este contexto en la empresa se preguntan, ¿cuánta arena
contienen realmente los costales? Para averiguarlo deciden tomar una muestra aleatoria de
30 costales de cada lote pedido (500 costales). Los pesos obtenidos en las muestras de los
últimos tres lotes se muestran a continuación. Las especificaciones iniciales que se
establecen para el peso de los costales de arena son 200.8 kg.
Lote Peso de costales de la muestra
18.6 19.2 19.5 19.2 18.9 19.4 19.0 20.0 19.3 20.0
1 19.1 18.6 19.4 18.7 21.0 19.8 19.0 18.6 19.6 19.0
19.6 19.4 19.8 19.1 20.0 20.4 18.8 19.3 19.1 19.1
18.6 19.9 18.8 18.4 19.0 20.1 19.7 19.3 20.7 19.6
2 19.5 19.1 18.5 19.6 19.4 19.6 20.3 18.8 19.2 20.6
20.0 18.4 18.9 19.7 17.8 19.4 18.9 18.4 19.0 19.7
20.1 20.2 21.0 19.7 20.1 20.0 19.1 20.4 19.6 20.6
3 20.0 19.7 20.8 19.7 19.7 20.4 19.8 20.5 20.0 20.0
20.2 19.7 20.0 19.6 19.7 19.8 19.9 20.3 20.4 20.2

42. a) Tomando en cuenta los 90 datos, ¿el centrado del proceso es adecuado?
b) ¿La variabilidad es poca o mucha? Apóyese en los estadísticos adecuados.
c) Obtenga un histograma para los noventa datos, inserte las especificaciones e interprételo
con detalle.
d) Dé su conclusión general sobre si los bultos cumplen con el peso especificado.
e) Haga un análisis de cada lote por separado y con apoyo de estadísticos y gráficas, señale si
hay diferencias grandes entre los lotes.
f) ¿Las diferencias encontradas se podrían haber inferido a partir del histograma del inciso c?
Costales
Media 19.562
Error típico 0.069
Mediana 19.6
Moda 20
Desviación estándar 0.65
Varianza de la muestra 0.42
Curtosis -0.29
Coeficiente de asimetría -0.07
Rango 3.2
Mínimo 17.8
Máximo 21
Suma 1760.6
Cuenta 90
Histograma "Peso de los Costales"
25
20
Frecuencia
15
10
5
0
Kilogramos

43. Análisis: Los datos que corresponden al peso de los costales se encuentran con muy poca
variabilidad, ya que esto es evidente por el coeficiente de asimetría, Curtosis y la desviación
estándar, cuyos valores se aproximan a cero. Se puede constatar que existe un ligero sesgo a la
izquierda.
Lote 1
Media 19.35
Error típico 0.10
Mediana 19.25
Moda 19.1
Desviación estándar 0.56
Varianza de la muestra 0.31
Curtosis 1.39
Coeficiente de asimetría 1.01
Rango 2.4
Mínimo 18.6
Máximo 21
Suma 580.5
Cuenta 30

44. Histograma "Lote 1"
14
12
Frecuencia 10
8
6
4
2
0
18.6 19.08 19.56 20.04 20.52 y mayor...
Kilogramo
Análisis: El lote 1, con respecto a la población total de los costales, cuenta con mayor variabilidad,
con una mayor concentración de los datos a la derecha de la media.
Lote 2
Media 19.2967
Error típico 0.1260
Mediana 19.35
Moda 18.4
Desviación estándar 0.69

45. Varianza de la muestra 0.48
Curtosis -0.26
Coeficiente de asimetría 0.06
Rango 2.9
Mínimo 17.8
Máximo 20.7
Suma 578.9
Cuenta 30
Histograma "Lote 2"
10
9
8
7
Frecuencia
6
5
4
3
2
1
0
17.8 18.38 18.96 19.54 20.12 y mayor...
Kilogramos

46. Análisis: El lote presenta mayor variabilidad en relación al 1 y 2 con sesgo a la derecha donde la
mayoría de los datos se concentran a la derecha y la curva normal presenta una forma ligeramente
achatada.
Lote 3
Media 20.04
Error típico 0.07
Mediana 20
Moda 19.7
Desviación estándar 0.40
Varianza de la muestra 0.16
Curtosis 0.46
Coeficiente de asimetría 0.29
Rango 1.9
Mínimo 19.1
Máximo 21
Suma 601.2
Cuenta 30
Histograma "Lote 3"
12
10
8
Frecuencia
6
4
2
0
19.1 19.48 19.86 20.24 20.62 y mayor...
Kilogramos

47. Análisis: El proceso se encuentra con una ligera variabilidad en los datos, con acantilado lo que
ocasiona que los mismos presenten variabilidad, debido a que los datos tiendan a agruparse más a
la derecha de la media causando una desviación de 0.4 y dándole una forma alargada a la curva
normal.
4. En una empresa que fabrica y vende equipo para fotocopiado utilizan como un indicador
importante de la calidad en el servicio posventa el tiempo de respuestas a solicitudes de
apoyo técnico debido a fallas en los equipos. Para problemas mayores, en cierta zona del
país, se ha establecido como meta que la respuesta se dé en un máximo de 6 horas hábiles;
es decir, de que habla el cliente solicitando apoyo, y que si el problema se clasifica como
grave no deben pasar más de 6 horas hábiles en que un técnico acuda a resolver su
problema. A continuación se aprecian los tiempos de respuestas en horas para los primeros
9 meses del año (65 datos).
5.0 5.4 7.1 7.0 5.5 4.4 5.4 6.6 7.1 4.2
4.1 3.0 5.7 6.7 6.8 4.7 7.1 3.2 5.7 4.1
5.5 7.9 2.0 5.4 2.9 5.3 7.4 5.1 6.9 7.5
3.2 3.9 5.9 3.6 4.0 2.3 8.9 5.8 5.8 6.4
7.7 3.9 5.8 5.9 1.7 3.2 6.8 7.0 5.4 5.6
4.5 6.5 4.1 7.5 6.8 4.3 5.9 3.1 8.3 5.4
4.7 6.3 6.0 3.1 4.8

48. a) Calcule las medidas de tendencia central y con base en éstas, ¿cree que se cumple con la
meta?
b) Haga un histograma e interprete sus aspectos más relevantes.
c) A partir del análisis que se ha hecho, ¿qué recomendaciones daría para ayudar a cumplir
mejor la meta?
Columna1
Media 5.37
Error típico 0.20
Mediana 5.5
Moda 5.4
Desviación estándar 1.62
Varianza de la muestra 2.62
Curtosis -0.52
Coeficiente de asimetría -0.20
Rango 7.2
Mínimo 1.7
Máximo 8.9
Suma 348.8
Cuenta 65
Histograma
18
16
14
12
Frecuencia
10
8
6
4
2
0
Tiempo de Respuesta

49. Análisis: Los datos correspondientes se encuentran con una variabilidad ligera donde la curva de la
normal tiende a ser achata y con colas muy cortas presentando un acantilado donde la mitad de los
datos son menor que 5.5 y la otra mitad son mayores o iguales a ese valor.
5. Los datos de la tabla siguiente representan las horas caídas de equipos, por semana, de tres
líneas de producción.
Semana Línea 1 Línea 2 Línea 3 Semana Línea 1 Línea 2 Línea 3
1 7.7 6.6 7.5 14 6.3 6.5 8.5
2 6.8 5.2 8.1 15 7.8 7.7 8.0
3 8.5 7.2 6.2 16 6.7 7.4 7.7
4 8.6 9.2 7.4 17 7.3 6.1 7.5
5 5.7 6.7 8.2 18 5.7 6.2 8.2
6 7.9 6.2 6.0 19 6.2 7.3 7.7
7 8.1 7.1 8.2 20 7.3 6.9 7.0
8 7.6 8.1 8.1 21 5.0 6.1 .5
9 7.1 6.4 6.7 22 5.0 6.9 6.2
10 7.3 6.3 8.0 23 5.4 8.4 6.0
11 7.8 8.2 8.1 24 7.5 5.0 6.1
12 6.1 8.4 8.1 25 6.0 7.4 5.8
13 6.4 7.4 7.0

50. a) Analice los datos para cada línea, anote las principales características de la distribución
de los datos.
b) Compare las tres líneas, ¿nota alguna diferencia importante?
Línea 1
Media 6.87
Error típico 0.21
Mediana 7.1
Moda 7.3
Desviación estándar 1.05
Varianza de la muestra 1.10
Curtosis -0.94
Coeficiente de asimetría -0.23
Rango 3.6
Mínimo 5
Máximo 8.6
Suma 171.8
Cuenta 25
Histograma "Línea 1"
9
8
7
6
Semanas
5
4
3
2
1
0
5 5.72 6.44 7.16 7.88 y mayor...
Horas Caídas

51. Análisis: La curva de la normal tiende a ser plana o achatada debido a como los datos se
encuentran distribuidos, aunque la deviación estándar no es grande en magnitud, sigue siendo un
problema muy grande ya que la variabilidad existe en el proceso y mientras la empresa no le de
solución va a seguir perdiendo tiempo, un factor importante para los clientes y así cumplir con los
tiempos de entrega. También presenta sesgo a la izquierda.
Línea 2
Media 7.00
Error típico 0.20
Mediana 6.9
Moda 7.4
Desviación estándar 1.00
Varianza de la muestra 1.00
Curtosis 0.01
Coeficiente de asimetría 0.13
Rango 4.2
Mínimo 5
Máximo 9.2
Suma 174.9
Cuenta 25

52. Histograma "Línea 2"
10
9
8
7
6
Semanas
5
4
3
2
1
0
5 5.84 6.68 7.52 8.36 y mayor...
Horas Caídas
Análisis: El coeficiente de asimetría nos muestra que hay mayor concentración de datos a la
derecha de la media y el coeficiente de Curtosis se aproxima mucho a 0 lo que nos dice que la
campada de Gauss se aproxima más a la curva normal deseada, curva que en este caso representa
el proceso en la línea 2.
Línea 3
Media 7.07
Error típico 0.32
Mediana 7.5
Moda 8.1

53. Desviación estándar 1.62
Varianza de la muestra 2.62
Curtosis 11.35
Coeficiente de asimetría -2.96
Rango 8
Mínimo 0.5
Máximo 8.5
Suma 176.8
Cuenta 25
Histograma "Línea 3"
18
16
14
12
Frecuencia
10
8
6
4
2
0
0.5 2.1 3.7 5.3 6.9 y mayor...
Clase
Análisis: La línea 3 presenta mayor variabilidad en su proceso, con acantilado y un coeficiente de
asimetría de -2.96 y cuyo coeficiente de Curtosis nos muestra que la curva es alargada en el centro.

54. 6. Una característica importante en la calidad de la leche de vaca es la concentración de grasa.
En una industria en particular se ha fijado como estándar mínimo que debe cumplir el
producto que recibe directamente de los establos lecheros, 3.0%. Por medio de muestreos
y evaluaciones en cierta época del año se obtuvieron los siguientes 90 datos sobre
concentración de grasa, en cierta región.
2.7 3.4 3.5 4.0 3.1 3.3 3.5 3.3 3.2 3.4 2.6 3.1
3.4 2.7 3.3 3.6 2.9 2.8 3.0 3.6 3.5 2.8 3.1 2.8
2.2 3.4 3.3 2.5 3.4 2.7 2.9 3.6 3.3 2.7 3.7 3.3
3.2 3.1 2.9 2.7 3.3 3.6 3.3 3.1 3.1 3.4 3.0 3.5
3.4 3.0 2.9 3.2 3.2 3.0 3.3 3.9 3.3 3.0 3.0 3.5
2.9 3.5 3.1 3.5 3.0 3.1 2.9 3.1 3.1 2.9 2.9 3.4
3.4 3.1 3.2 3.3 3.2 3.3 3.0 3.2 3.5 3.4 3.8 3.2
2.9 3.0 3.2 3.2 3.3 3.8
a) Calcule las medidas de tendencia central y de variabilidad, y comente sobre el
cumplimiento del estándar mínimo para la concentración de la grasa.
b) Obtenga un histograma, inserte el estándar mínimo e interprete ampliamente.
c) La población de donde provienen estos datos, ¿cumple el estándar mínimo?
Columna1
Media 3.19
Error típico 0.03
Mediana 3.2
Moda 3.3
Desviación estándar 0.32
Varianza de la muestra 0.10
Curtosis 0.52
Coeficiente de asimetría -0.15
Rango 1.8
Mínimo 2.2
Máximo 4
Suma 286.9
Cuenta 90

55. Histograma
25
20
Frecuencia
15
10
5
0
Concentración
Análisis: Aquí los datos obtenidos sobre el nivel de concentración de grasa en la leche de vaca
presentan poca variabilidad donde la curva normal tiende a ser un poco alargada.
7. A continuación se muestran 100 datos obtenidos en las pruebas destructivas de la
resistencia de botellas.
28.3 26.8 26.6 26.5 28.1 24.8 27.4 26.2 29.4 28.6 24.9 25.2
30.4 27.7 27.0 26.1 28.1 26.9 28.0 27.6 25.6 29.5 27.6 27.3

56. 26.2 27.7 27.2 25.9 26.5 28.3 26.5 29.1 23.7 29.7 26.8 29.5
28.4 26.3 28.1 28.7 27.0 25.5 26.9 27.2 27.6 25.5 28.3 27.4
28.8 25.0 25.3 27.7 25.2 28.6 27.9 28.7 25.3 29.2 26.5 28.7
29.3 27.8 25.1 26.6 26.8 26.4 26.4 26.3 28.3 27.0 23.7 27.7
26.9 27.7 26.2 27.0 27.6 28.8 26.5 28.6 25.7 27.1 27.8 24.7
27.1 26.4 27.2 27.3 27.0 27.7 27.6 26.2 24.7 27.2 23.8 27.4
29.5 26.4 25.8 26.7
a) Calcule medidas de tendencia central y de variabilidad.
b) Estime los límites reales y comente si las botellas cumplen la resistencia mínima e
interprete ampliamente.
c) Obtenga un histograma, inserte la resistencia mínima e interprete ampliamente.
d) Con base en los análisis anteriores, dé su opinión sobre si el proceso cumple con la
especificación inferior.
Columna1
Media 27.10
Error típico 0.14
Mediana 27.1
Moda 27.7
Desviación estándar 1.39
Varianza de la muestra 1.93
Curtosis -0.10
Coeficiente de asimetría -0.18
Rango 6.7
Mínimo 23.7
Máximo 30.4
Suma 2709.5
Cuenta 100
LRS 31.26
LRI 22.93

57. Histograma
25
20
Frecuencia
15
10
5
0
Resistencia de las Botellas
Análisis: La información obtenida de las pruebas destructivas para ver la resistencia de las botellas
tiene mucha variabilidad ya que la desviación estándar así lo indica, donde la curva normal tiende a
ser achatada.
8. En la elaboración de una bebida se desea a garantizar que el porcentaje de CO2 esté entre
2.5 y 3.0. De los datos obtenidos del monitoreo del proceso se obtuvieron los siguientes
115 datos.

58. 2.61 2.56 2.63 2.61 2.56 2.60 2.56 2.60 2.55 2.64 2.66 2.65
2.69 2.51 2.56 2.64 2.52 2.57 2.60 2.67 2.48 2.57 2.66 2.59
2.61 2.61 2.66 2.64 2.56 2.58 2.61 2.57 2.56 2.59 2.67 2.57
2.57 2.49 2.58 2.69 2.61 2.64 2.57 2.55 2.70 2.65 2.67 2.65
2.73 2.65 2.58 2.67 2.53 2.67 2.62 2.57 2.64 2.55 2.64 2.52
2.60 2.67 2.71 2.51 2.57 2.57 2.51 2.67 2.50 2.56 2.65
2.61 2.49 2.66 2.52 2.60 2.63 2.61 2.60 2.56 2.67 2.61
2.62 2.52 2.72 2.53 2.64 2.52 2.60 2.53 2.62 2.64 2.60
2.53 2.61 2.68 2.59 2.63 2.66 2.59 2.58 2.65 2.57 2.52
2.64 2.55 2.63 2.59 2.62 2.52 2.49 2.55 2.60 2.61 2.58
a) Con medidas de tendencia central señale si la tendencia central de las mediciones es
adecuada.
b) Calcule las desviaciones estándar y una aproximación de los límites reales y con base en
éstos decidida si la variabilidad de los datos es aceptable.
c) Obtenga un histograma e interprételo.
d) Con la evidencia obtenida antes, cuál es su opinión sobre la capacidad del proceso referido.
Columna1
Media 2.599
Error típico 0.005
Mediana 2.600
Moda 2.610
Desviación estándar 0.056
Varianza de la muestra 0.003
Curtosis -0.587
Coeficiente de asimetría -0.030
Rango 0.250
Mínimo 2.480
Máximo 2.730
Suma 298.870
Cuenta 115

59. Histograma
25
20
Frecuencia
15
10
5
0
Porcentaje de CO2
Análisis: Se puede decir, en este caso, que la variabilidad de los datos con respecto al porcentaje de
CO2 es mínima, lo que es indicado por la desviación, la asimetría y el coeficiente de Curtosis,
donde se ve que los datos tienden a estar centrados con poca variabilidad.

60. CAPÍTULO 6
1. En un proceso de manufactura las piezas resultan defectuosas por distintas razones. Para
entender cuál es la regularidad estadística de esta problemática se decide registrar los datos
de la inspección. Para el diseño de la hoja de verificación se toma en cuenta que las
posibles fuentes de variabilidad (origen de los problemas) son las máquinas, el día y el
turno. En la siguiente tabla se muestran los datos obtenidos en una semana.
Lunes Martes Miércoles Jueves Viernes
Máquina
AM PM AM PM AM PM AM PM AM PM
A oo O ooo o ooooo ooooo ooo o ooo
x X xx xxx xxx x xx xx
- - / -- / //
B oooo oooo ooo oooooo oooooooo oooooooo ooooo oooo ooooo ooo
xx xxx xx xx - xx xx xx x
- - -/ x --/ - /
C oo O oo oooooo oooooo oo o oo oo
x x / x
- * /
D oo O oo oo ooo oooo oo oo oo o
x x / * / x * ** ***
* - /
(o) Rasguños superficiales, (x) Rupturas, (-) Incompletas, (/) Forma inapropiada, (*) Otro.
a) Realice un Pareto para problemas y encuentre cuál es el predominante.
b) Para el defecto principal, realice Paretos de segundo nivel en función de:
 Máquinas.
 Día.
 Turno.
c) De los Paretos de segundo nivel, ¿con cuáles se encontró pistas específicas para localizar la
causa? Explique.

61. d) En resumen, ¿cuáles son las pistas concretas para orientar los esfuerzos de mejora?
Pareto de Problemas
Frecuencia
Problema Frecuencia % Frecuencia
Acumulada
Rasguños superficiales 119 62% 62%
Rupturas 39 20% 82%
Incompletas 13 7% 89%
Forma inapropiada 12 6% 95%
Otros 9 5% 100%
Total 192 100%
Diagrama de Pareto
140 120%
120 100%
Frecuencia
100 80%
80 60%
60
40 40%
20 20% Frecuencia
0 0%
Frecuencia
acumulada
Tipo de Defecto

62. Análisis: El problema de rasguños superficiales y las rupturas cusan el 82% de los problemas, de
los cuales el primero constituye el 62% y ese es el problema que debe tener prioridad para ser
erradicado.
Pareto de Máquinas
% Frecuencia
Máquinas Frecuencia
Frecuencia Acumulada
B 50 42% 42%
A 24 20% 62%
C 24 20% 82%
D 21 18% 100%
Total 119 100%
Diagrama de Pareto
60 120%
50 100%
40 80%
Frecuencia
Frecuencia
30 60%
Frecuencia
20 40% acumulada
10 20%
0 0%
B A C D
Máquina

63. Análisis: Las máquinas B, A y C generan el 82% de los problemas que surgen en el proceso, ya sea
por averías o fallas. De ellas la que produce mayor cantidad de problemas es la B, donde debería
de hacerse un estudio y determinar si las fallas son de origen humano o tecnológico.
Pareto de Días
% Frecuencia
Día Frecuencia
Frecuencia Acumulada
Miércoles 45 38% 38%
Jueves 20 17% 55%
Martes 19 16% 71%
Viernes 18 15% 86%
Lunes 17 14% 100%
Total 119 100%

64. Diagrama de Pareto
50 120%
40 100%
Freceuncia
80%
30
60%
20 Frecuencia
40%
10 20%
0 0% Frecuencia
acumulada
Día
Análisis: Los días en los que se hacen presentan la mayor cantidad de fallas son el miércoles,
jueves, martes y viernes. Es en esos días donde se producen 82% de los problemas que hay en el
proceso.

65. Pareto de Turnos
% Frecuencia
Turnos Frecuencia
Frecuencia Acumulada
I 66 55% 55%
II 53 45% 100%
Total 119 100%
Pareto de Turnos
70 120%
60 100%
50
Frecuencia
80%
40 Frecuencia
60%
30
20 40%
20% Frecuencia
10
acumulada
0 0%
I II
Turno
Análisis: El turno en el que se dan la mayor cantidad de problemas es el turno I, donde se generan
el 55% de los problemas y es en el que se tiene que investigar la causas por las cuales se originan
dichas fallas.

66. 2. En una fábrica de aparatos de línea blanca se han tenido problemas con la calidad de las
lavadoras. Un grupo de mejora de la calidad decide revisar los problemas de la tinta de las
lavadoras, ya que frecuentemente es necesario retrabajarla para que ésta tenga una calidad
aceptable. Para ello estratificaron los problemas en la tina de lavadora por tipo de defecto,
con la idea de localizar cuál es el defecto principal. A continuación se muestra el análisis de
los defectos encontrados en las tinas producidas en cinco meses. Realice un análisis de
Pareto y obtenga conclusiones.
Defecto Frecuencia
Ovalada la boca de la tina 1,200
Perforaciones deformes 400
Boca de tina despostillada 180
Falta de fundente 130
Mal soldada 40
Total 1,950
Defecto Frecuencia % Frecuencia Frecuencia
acumulada
Boca de la tina ovalada 1200 62% 62%
Perforaciones deformes 400 21% 82%
Boca de la tina despostillada 180 9% 91%
Falta de fundente 130 7% 98%
Mal soldada 40 2% 100%
Total 1950 100%

67. Diagrama de Pareto
1500 120%
Frecuencia
100%
1000 80%
60%
500 40% Frecuencia
20%
0 0%
Frecuencia
acumulada
Defecto
Análisis: Los defectos principales en las tinas de lavadora son que la boca de las mismas sea
ovalada o que tenga perforaciones deformes ya que constituyen el 82% de los problemas y es aquí
donde se deben concentrar los esfuerzos para reducir tales defectos.
3. En cierta empresa es usual pagar horas extras para cumplir con los tiempos de entrega. En
este centro productivo, un grupo de mejora de calidad está tratando de reducir la
proporción de piezas malas. Con este propósito deciden investigar la relación entre la

68. cantidad de horas extras, X, y el porcentaje de artículos defectuosos, Y. A continuación se
muestran los datos obtenidos.
Porcentaje de
Semana Horas extras
defectuosos
1 340 5
2 95 3
3 210 6
4 809 15
5 80 4
6 438 10
7 107 4
8 180 6
9 100 3
10 550 13
11 220 7
12 50 3
13 193 6
14 290 8
15 340 2
16 115 4
17 362 10
18 300 9
19 75 2
20 93 2
21 320 10
22 154 7
a) Obtenga el diagrama de dispersión para estas variables.
b) ¿Qué relación observa?
c) Con base en lo anterior, ¿puede concluir con seguridad que cuando se trabaja tiempo extra
se incrementa el porcentaje de defectuosos, porque ocurren factores como calentamiento

69. de equipo, cansancio de obreros, etc., que causan mayores problemas en la calidad de las
piezas?
18
16 y = 0.0171x + 2.111
R² = 0.7368
14
12
10
Series1
8
Lineal (Series1)
6
4
2
0
0 200 400 600 800 1000
Análisis: La relación existen entre la cantidad de horas extras y el número de defectos es lineal
positiva, lo que quiere decir que a más horas de trabajo mayores defectos, ya que por el cansancio
los trabajadores van a laborar sin motivación alguna.
4. En una empresa del ramo gráfico se ha llevado durante dos meses el registro del tipo de
defectos que tienen los productos finales, obteniéndose los siguientes problemas con sus
respectivos porcentajes: fuera de tono, 35%; manchas, 30%; fuera de registro, 15%; mal
corte, 12%; código de barras opaco, 8%. De acuerdo con el principio de Pareto, ¿se puede
decir que el problema vital, desde el punto estadístico, es fuera de tono?
Problemas % Frecuencia F. acumulada
Fuera de tono 35% 35%
Manchas 30% 65%
Fuera de registro 15% 80%
Mal corte 12% 92%
Código de barras opaco 8% 100%
Total 100%
Análisis: Realmente el 80% de los problemas no es únicamente causado por fallas fuera de tono,
sino también por manchas y errores fuera de registro.

70. CAPÍTULO 7
1. Según la información proporcionada por cada carta X-R sobre un proceso de producción
de piezas metálicas, la media de la longitud de tales piezas es 50mm y el rango medio con
tamaño de muestra 5, es 0.6; conteste:
a) Obtenga la desviación estándar del proceso.
b) Calcule los límites de control para la carta X (tamaño de sub-grupo 5) e interprételos.
c) También obtenga los límites de control para la carta R y explique su significado práctico.
d) Si la especificación inferior y superior para esta pieza es 49 y 51 mm, respectivamente;
calcule los límites reales o naturales e interprételos.
e) Explique para qué sirven los límites que obtuvo en los incisos b y c y para qué los que
obtuvo en el inciso d.
f) ¿El proceso es capaz? Argumente.
g) ¿Tiene información suficiente para comprobar si el proceso es estable (está en control
estadístico)? Explique y argumente.
Límites de Control, Carta X
LCS 50.3462
LCI 49.6538
LCC 50
Límites de Control, Carta R
LCS 0.6
LCI 0.6
LCC 0.6
Límites Naturales
LRS 50.7739
LRI 49.2261
Interpretación: Los límites de la carta X establecen de donde a donde deben estar ubicados los
datos de un proceso con respecto a la centralidad del mimo y los límites de la carta R miden la
variabilidad de los mismos. Y para poder comprobar si la estabilidad del proceso es estable se
necesita recolectar datos procedentes del proceso.

71. 2. El peso ideal del contenido neto de una caja de cereal es de 250.0g, y se tiene una
tolerancia de ±2.5 g. Para monitorear tal peso se usa una carta de control X–R. de datos
históricos se tiene que la media y la desviación estándar del proceso son µ = 249.0 y σ =
0.70, respectivamente. Con esta información conteste las siguientes preguntas:
a) ¿Cuáles son las especificaciones para el peso? Y explique por qué es importante
cumplirlas. Las especificaciones del peso son:
ES 252.5
EI 247.5
Las especificaciones son importantes porque son dadas por los clientes, por quienes la
empresa funciona.
b) Explique en forma y con sus palabras, ¿Qué se le controla al peso con la carta X y que
con la carta R? Considerando un tamaño de subgrupo de 4, obtenga la línea central y
los límites de control para la correspondiente carta X, e interprete.
LCS 4.223
LCI 0.578
LCC 2.4
Con la carta X se mide cuán centrado está el proceso y con la carta R la variabilidad que hay en el
mismo.
3. En una empresa en la que se fabrican corcholatas o tapas metálicas para bebidas gaseosas,
un aspecto importante es la cantidad de PVC que lleva cada corcholata, el cual determina el
espesor de la película que hace que la bebida quede bien cerrada. El peso de los gránulos
de PVC debe estar entre 212 y 218 mg. Si el peso es menor a 212 mg, entonces, entre otras
cosas, la película es muy delgada y eso puede causar fugas de gas en la bebida. Pero si el
peso es mayor a 218 g, entonces se gasta mucho PVC y aumentan los costos. Para asegurar
que se cumple con especificaciones, de manera ordinaria se usa una carta de control: cada
30 minutos se toma una muestra de cuatro gránulos consecutivos de PVC y se pesan. En la
siguiente tabla se muestran las últimas 25 medias y los rangos obtenidos del proceso.
Subgrupos Media Rango

72. 1 214.18 2.5
2 213.48 2.7
3 213.98 2.2
4 214.12 1.8
5 214.46 2.5
6 213.38 2.7
7 213.56 2.3
8 214.08 1.8
9 213.72 2.9
10 214.64 2.2
11 213.92 2.4
12 213.96 3.6
13 214.2 0.4
14 213.74 3.2
15 214.26 1.2
16 214.18 2.2
17 214.0 1.0
18 213.6 2.0
19 214.2 2.7
20 214.38 0.8
21 213.78 2.0
22 213.74 1.6
23 213.32 2.4
24 214.02 3.2
25 214.24 1.1
Media 213.966 2.136
a) Calcule los límites de una carta X-R y obtenga las cartas.
b) Interprete las cartas (puntos fuera, tendencias, ciclos, etcétera)
c) ¿El proceso muestra una estabilidad o estado de control estadístico razonable?
d) Analice la capacidad del proceso, para ello:
a. Calcule los límites reales del proceso e interprételos.
Interpretación: El proceso de fabricación de las corcholatas se encuentra fuera de control
estadístico en cuanto a su centrado ya que no se cumplen una serie de criterios para poder afirmar
su estabilidad y buen funcionamiento. En la carta X 13 puntos se encuentran fuera de control
estadístico pero sin embargo, en la carta R se cumple con los niveles de variabilidad en el mismo.

73. Carta X
235
230
225
Promedio
220
LCS
215 LCI
LC
210
205
200
1 3 5 7 9 11 13 15 17 19 21 23 25
LCS 216.97
LCI 213.85
LCC 215.41
A2 0.729

74. Carta R
6
5
4
Rango
3 LCS
LCI
2 LC
1
0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
LCS 4.874779
LCI 0
LCC 2.136
d3 0
d4 2.2822

75. 4. En el caso de la longitud de las bolsas del ejercicio 11, se decide emplear una carta de
control X – R utilizando un tamaño de subgrupo de cinco, en donde se toman cinco bolsas
consecutivas cada determinado tiempo. En la siguiente tabla se muestran las medias y los
rangos de los últimos 40 subgrupos (los datos están en milímetros)
a) Calcule los límites de una carta X – R y obtenga las cartas.
b) Interprete las cartas (puntos fuera, tendencias, ciclos, altas variabilidad, etc.).
Subgrupo Media Rango Subgrupo Media Rango
1 301.12 1.9 21 302 4.6
2 300.96 1 22 299.02 3.5

76. 3 301.16 3.6 23 299.5 3.1
4 300.5 1 24 300.3 2.3
5 301.28 2.5 25 301.64 3.4
6 299.92 2.3 26 300.88 2.9
7 300 2.3 27 301.28 1.8
8 301.86 1.5 28 300.75 1.5
9 301.52 2.3 29 301.6 3.1
10 302.8 0.4 30 300.53 2.8
11 299.01 3 31 300.41 1.4
12 300.02 2.5 32 300.19 2.1
13 300.1 2.3 33 301.12 3.4
14 301.28 3.4 34 300.8 3.2
15 301.02 1.1 35 300.27 3.4
16 300.7 3.9 36 300.91 2.7
17 301.2 3.1 37 300.48 3.2
18 300.96 3.1 38 302 1.8
19 300.24 3.7 39 299.22 3.5
20 301.86 2.7 40 300.59 3
Carta X
n 40
A2 0.153
X 300.775
LCS 301.174
LCI 300.376
LCC 300.775
R 2.608
Interpretación: En la carta X se puede apreciar como varios puntos se encuentran fuera de control
estadístico, lo que hace al proceso impredecible ya que se rompe el criterio 14, además se puede
apreciar en la gráfica los cambios bruscos que hay dentro del proceso, y esto es algo que se debe
erradicar totalmente de dicho proceso.

77. 304
303
302
Media
301
LCS
300 LCI
LCC
299
298
297
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39
Carta R
n 40
D3 0.4597
D4 1.5403

78. LCS 1.199
LCI 4.016
LCC 2.608
R 2.608
5
4
Rango
3
LCS
2 LCI
1 LCC
0
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39
Interpretación: La longitud de las bolsas en cuanto a su variabilidad se encuentran fuera de control
estadístico, ya que al igual que la carta X no se cumplen muchos criterios y la variabilidad
experimenta muchas subidas y caídas bruscas.
5. Se desea que la resistencia de un artículo sea de por los menos 300 psi. Para verificar que
se cumple con tal característica de calidad, se hacen pequeñas inspecciones periódicas y los
datos se registran en una carta X-R. El tamaño de subgrupo que se ha usado es de tres
artículos, que son tomados de manera consecutiva cada dos horas. Los datos de los últimos
subgrupos se muestran en la tabla 7.5. Conteste:
a) ¿Dado que la media de media es 320.73, el proceso cumple con las especificación inferior
(El=300)? Explique.
b) Calcule los límites de la Carta X-R, e interprételos.
c) Obtenga las cartas e interprételas.
Subgrupo Datos Media Rango
1 315.6 319.2 303.8 312.87 15.4
2 218.8 309.2 321.4 316.47 12.2
3 311.2 312.1 342.9 322.07 31.7
4 322.0 321.1 329.1 324.07 8.0
5 315.2 327.4 300.6 314.40 26.8
6 310.3 319.8 338.5 322.87 28.2
7 320.6 315.9 318.3 318.27 4.7

79. 8 322.2 303.6 323.4 316.40 19.8
9 329.1 306.7 312.4 316.07 22.4
10 322.4 318.8 299.7 313.63 22.7
11 326.2 310.1 338.5 324.93 28.4
12 328.8 325.0 322.0 325.27 6.8
13 328.8 306.3 305.6 313.57 23.2
14 318.7 320.8 310.3 316.60 10.5
15 326.7 316.7 327.3 323.57 10.6
16 313.4 307.4 329.5 316.77 22.1
17 337.3 312.9 324.4 324.87 24.4
18 316.3 314.1 323.0 317.80 8.9
19 327.2 338.2 340.9 335.43 13.7
20 337.8 343.0 337.4 339.40 5.6
21 309.2 321.7 310.5 313.80 12.5
22 314.3 321.6 318.0 317.97 7.3
23 318.9 322.2 333.5 324.87 14.6
24 303.7 326.3 337.1 322.37 33.4
25 319.3 338.8 320.9 326.33 19.5
26 317.0 327.4 312.5 318.97 14.9
27 310.6 318.5 336.7 321.93 26.1
28 319.5 326.0 333.2 326.23 13.7
29 308.6 321.7 306.0 312.10 15.7
30 316.2 321.6 328.5 322.10 12.3
320.73 17.2
Carta X
n 3
A2 1.023
Gran Media 320.73
LCS 338.331
LCI 303.133
LCC 320.732
R 17.203
350
340
330
Promedio
320
LCS
310 LCI
300 LCC
290
280
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29

80. Interpretación: La resistencia de los artículos se encuentra fuera de control estadístico ya que se
cumplen los criterios 1, 3 y 14 que hacen que dicho proceso sea impredecible estadísticamente. En
cuanto a su centralidad dicho proceso está fuera de control.
Carta R
d4 2.5735
d3 0
R 17.20
LCS 44.27
LCI 0
LCC 17.20

81. 50
45
40
35
Rango
30
LCS
25
LCI
20
15 LCC
10
5
0
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29
Interpretación: En cuanto a la variabilidad en la resistencia de los artículos estos se encuentran
dentro de control estadístico ya que ninguno de los puntos sale de los límites de control.

82. 6. Una empresa que hacen impresiones en láminas de acero que después se convierten en
recipientes de productos de otras empresas. Un aspecto importante a vigilar en dicha
impresión es la temperatura de “Horneado”, donde, entre otras cosas, se da adherencia y
se seca la lámina una vez que ha sido impresa. En una fase particular de la horneada se
tiene que la temperatura de cierto horno debe ser 125 grados centígrados, con una
tolerancia de más menos 5 grados centígrados. Si no se cumple con tal rango de
temperatura, entonces se presentan problemas en la calidad final de la impresión. A pesar
que el horno se la programa la temperatura, en la tabla 7.9 se muestran los últimos 45 datos
en el orden que se obtuvieron, con el rango móvil para facilitar cálculos.
a) ¿Por qué utilizar en este caso una carta de individuales y no una carta X-R?
b) Estime los límites de control para la carta de individuales e interprételos.
c) Obtenga la carta e interprétela.
d) En el punto 32 se decidió hacer un ajuste al horno, ¿tiene algún fundamento estadístico la
decisión de hacer el ajuste? ¿la decisión fue oportuna?
e) Alguien no está del todo de acuerdo en la decisión tomada, argumentando que la
temperatura todavía estaba dentro de especificaciones, ¿Qué opina al respecto?
Rango Rango
Subgrupo Temperatura Subgrupo Temperatura
Móvil Móvil
1 27.4 24 26.5 2.7
2 26.8 0.6 25 23.3 3.2
3 24.3 2.5 26 23.8 0.5
4 26.6 2.3 27 25.5 1.7
5 26.5 0.1 28 26.4 0.9
6 25.6 0.9 29 27.5 1.1
7 25.1 0.5 30 27.7 0.2
8 26.5 1.4 31 28.5 0.8
9 25.8 0.7 32 29.8 1.3
10 24.7 1.1 33 25.1 4.7
11 23.3 1.4 34 25.0 0.1
12 23.3 0.0 35 22.9 2.1
13 24.7 1.4 36 23.6 0.7
14 23.4 1.3 37 24.7 1.1
15 27.4 4.0 38 24.4 0.3
16 24.7 2.7 39 25.4 1.0
17 21.7 3.0 40 23.5 1.9
18 26.7 5.0 41 27.8 4.3

83. 19 24.2 2.5 42 25.5 2.3
20 25.5 1.3 43 26.4 0.9
21 25.3 0.2 44 24.5 1.9
22 25.0 0.3 45 23.5 1.0
23 23.8 1.2 Media 25.32 1.57
d2 1.1218
LCS 29.55975
LCI 21.08914
LCC 25.32
35
30
25
Temperatura
20
LCS
15 LCI
10 LC
5
0
1 3 5 7 9 111315171921232527293133353739414345
Interpretación: El proceso de horneado se encuentra fuera de control estadístico ya que la
variación en la temperatura hace que uno de los puntos se salga de los límites de control
establecidos.

84. 7. En una empresa se lleva el registro por consumo de agua por semana, y de acuerdo con los
datos históricos se sabe que μ= 170.2 metros cuadrados con σ=10.4.
a) Es mejor llevar el control de esta variable a través de una carta de control. ¿Por qué?
b) Obtenga los límites de control para la carta de individuales e interprételos.
c) ¿Cómo se detectaría en la carta los efectos de un programa de ahorro de agua?
LCS 201.4
LCI 167.2
LC 170.2
8. En el departamento de sistemas se lleva un registro del tiempo de respuesta a solicitudes de
servicio de clientes internos. Los últimos datos en horas y en el orden de ocurrencia se
muestran a continuación (el orden es por región).
39 92 38 33 119 32 96 32
35 34 42 39 78 37 26 32
38 43 46 37 28 40 35
35 41 37 44 37 34 43
42 86 117 43 42 33 37
98 126 31 40 52 29 71
49 57 33 34 34 23 36
42 27 33 37 37 96 29
39 87 109 37 122 33 62
a) ¿Es apropiado analizar estos datos mediante una carta de individuales?
b) Organice los datos en columna y obtenga la columna de rangos móviles de orden dos.

85. c) Obtenga los límites de control para una carta de control de individuales e interprételos.
d) Obtenga la carta de control e interprétela.
e) ¿El tiempo de respuesta es estable?
f) Grafique los datos en un histograma.
g) Observe cómo se aprecia en el histograma lo especial percibido en la carta, comente.
h) ¿Cuál sería su conclusión sobre la causa de los que se puede observar de especial?
d2 1.128
LCS 48.97
LCS 50.89
LCC 49.92
140
120
Respuesta de
100
solicitudes
80
LCS
60
40 LCI
20
LC
0
1 4 7 10131619222528313437404346495255586164
-20
-40

86. 9. En el departamento de capacitación de una empresa se lleva un registro por alumno del
porcentaje de asistencia a cada evento de capacitación. Con el total de alumnos que asisten
a cada curso. A continuación se muestran los resultados de los últimos 30 cursos:
71 74 79 65 85 76 76 61 74 78
78 99 70 76 88 78 82 67 72 76
70 79 71 74 80 70 83 69 77 75
71 72 75 71 70 73 69 74 77 78
78 79
a) Organice los datos en columna y obtenga la columna de rangos móviles de orden dos.
b) Analizar estos datos mediante una carta de individuales.
c) Obtenga la carta de control e interprétela.
d) ¿Se puede considerar satisfactoria la calidad de los cursos?
e) ¿Qué observa de especial en la carta?
f) ¿Cuáles podrían ser las razones de los puntos especiales?
g) ¿Qué límites de control utilizaría a futuro, de tal forma que reflejen la realidad
prevaleciente?
h) ¿A su juicio cuáles podrían las causes comunes que contribuyen al nivel de ausentismo
observado?
d2 1.128
LCS 94.57
LCI 55.91
LCC 75.24

87. 120
100
80
Asistencia
60 LCS
LCC
40
LCI
20
0
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41

88. CAPÍTULO 8
1. En una empresa del ramo metalmecánico se fabrican válvulas. Después del proceso de
fundición se hace una inspección y las piezas que no cumplen con ciertas características son
rechazadas. Las razones por las que pueden ser rechazadas son diversas: piezas
incompletas, porosas, mal formadas, etcétera. Para evaluar la variabilidad y la magnitud de
la proporción de piezas defectuosas en el proceso de fundición se decide implementar una
carta p. el proceso de fundición se hace por lotes. Aunque regularmente el tamaño de lote
es fijo, n=300, en ocasiones por diferentes motivos en algunos lotes se hacen unas cuantas
piezas de más o de menos. En la siguiente tabla se muestran los datos obtenidos durante
una semana para un cierto tipo de válvulas.
Lote Tamaño de lote Defectuosas Proporción
1 300 15 0.050
2 300 12 0.040
3 300 15 0.050
4 300 7 0.023
5 300 16 0.048
6 300 6 0.020
7 300 18 0.060
8 280 10 0.036
9 290 9 0.031
10 300 15 0.050
11 300 9 0.030
12 300 4 0.013
13 300 7 0.023
14 300 9 0.030
15 305 5 0.016
16 295 15 0.051
17 300 19 0.063
18 300 7 0.023
19 300 12 0.040
20 300 10 0.033

89. 21 300 4 0.013
Total 6,300 224
a) Calcule los límites de control utilizando el tamaño de subgrupo (lote) promedio.
b) ¿Cómo explicaría los límites de control a alguien que no tiene conocimientos profundos de
estadística?
c) Grafique la carta correspondiente e interprétela.
d) ¿El proceso es estable?
e) ¿Se puede considerar que la calidad del proceso es aceptable? Argumente.
n 21
LCS 0.0674
LCI 0.0034
LC 0.03538
0.08
0.07
0.06
0.05 Proporción, p¡
0.04 LCS
0.03 LCI
0.02 LC
0.01
0
1 3 5 7 9 11 13 15 17 19 21

90. 2. En el caso del ejercicio 5:
a) Suponga que todos los lotes tienen el mismo tamaño (el promedio), calcule los límites
de control para una carta np, e interprételos.
b) Grafique la correspondiente carta np y analícela.
c) ¿El proceso es estable?
d) ¿Observa alguna diferencia importante entre la carta p y la np?
e) ¿Cuál, carta p o la np sería la más conveniente en este caso? Argumente.
n 300
N° Lotes 21
p-promedio 0.036
LCS 20.29
LCC 10.67
LCI 1.044
np 10.67
25
Componentes
20 Defectuosos
15 LCS
10
LCC
5
LCI
0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

91. 3. En un proceso se lleva una carta p, cuya línea central es 0.08. Si se toma un lote de 100
artículos y se obtienen 16 defectuosos, ¿ese lote es anormal?, es decir, ¿en la producción
de ese lote el proceso estuvo fuera de control estadístico? Conteste calculando los límites
de control considerando n= 100 y p= 0.08.
n 100
p 0.08
Defectos totales 16
p-promedio 16%
LCS 27%
LCI 5%
LCC 16%

92. 4. En un proceso de producción se produce por lotes de tamaño 500, en la inspección final
de los últimos 30 lotes se obtuvieron la siguiente cantidad de artículos defectuosos.
Lote Tamaño Lote Tamaño
1 11 16 11
2 12 17 20
3 15 18 15
4 17 19 12
5 11 20 17
6 10 21 18
7 13 22 14
8 25 23 10
9 17 24 8
10 13 25 10
11 11 26 6
12 12 27 7
13 17 28 5
14 8 29 9
15 12 30 6
a) Calcule los límites de control para una carta p.
b) Grafique la carta p e interprétela.
c) ¿El proceso es estable?
d) Con sus palabras diga que significan los límites de control y la línea central.
e) A partir del lote 20 se empezó a ejecutar un plan de mejora, ¿hay algún tipo de evidencia
de que el plan haya dado resultado?
p 2.48%
LSC 4.57%
LIC 0.39%

93. 0.06
0.05
Fracción defectuosa
p
0.04
LCS
0.03
LCI
0.02
LCC
0.01
0
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29

94. 5. En una empresa se ha usado una carta p para analizar la variación en la proporción de
artículos defectuosos.
a) Si la línea central de esta carta es 0.05, el tamaño de subgrupo es de 150, calcule los límites
de control de la carta e interprételos.
b) Si la proporción de defectuosos de nueve lotes consecutivos de tamaño 150, fueron los
siguientes: 0.02, 0.065, 0.07, 0.08, 0.09, 0.07, 0.11, 0.10, 0.09. Analice estos datos con los
datos del inciso anterior y señale si en la producción de estos lotes el proceso estuvo en
control estadístico o si hubo algún cambio importante.
c) Haga lo mismo que el inciso a pero utilizando un tamaño de subgrupo de 300, e interprete
los límites que obtenga.
d) ¿Qué efecto tiene el tamaño de subgrupo en la amplitud de los límites de control de una
carta p?
LCS 0.103
LCC 0.05
LCI 0
n 150
Lote Proporción LCS LCI LCC
1 0.02 0.12 0.03 0.08
2 0.07 0.12 0.03 0.08
3 0.07 0.12 0.03 0.08
4 0.08 0.12 0.03 0.08
5 0.09 0.12 0.03 0.08
6 0.07 0.12 0.03 0.08
7 0.11 0.12 0.03 0.08
8 0.10 0.12 0.03 0.08
9 0.09 0.12 0.03 0.08
p-promedio 0.08

95. 0.14
0.12
0.10
Proporción
0.08
LCS
0.06 LCI
0.04 LCC
0.02
0.00
1 2 3 4 5 6 7 8 9

96. 6. Para analizar el desempeño de un proceso y tratar de mejorarlo, se decide analizar la
proporción de defectuosos. Para ello se toman subgrupos de tamaño 200 y se cuantifica la
cantidad de defectuosos. Los datos obtenidos durante 6 días son los siguientes:
Lote Defectuosos Lote Defectuosos
1 10 11 10
2 6 12 9
3 12 13 13
4 7 14 9
5 9 15 11
6 6 16 6
7 8 17 15
8 9 18 7
9 8 19 4
10 6 20 8
a) Calcule lo límites de control para una carta p, y explique el significado de los límites de
control que obtuvo.
b) Mediante una carta p analice los datos y obtenga conclusiones.
c) De acuerdo a los costos de producción el nivel de defectuosos máximo tolerable es de 5%.
Con base en esto alguien sugiere que el límite de control superior de la carta p debe ser
0.05, ¿es correcta esa sugerencia?
LCS 0.086
LCC 0.043
LCI 0.0
0.100
0.080
Proporción
0.060
LCS
0.040
LCC
0.020 LCI
0.000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

97. 7. En el caso del ejercicio anterior, se aplica un plan de mejora, y se toman varias acciones.
Los datos obtenidos en la semana posterior a las mejoras son:
Lote Defectuosos Lote Defectuosos
1 7 11 4
2 4 12 6
3 5 13 4
4 5 14 6
5 6 15 4
6 4 16 5
7 3 17 8

98. 8 4 18 3
9 7 19 7
10 6 20 8
a) Utilizando los límites de control obtenidos antes de la mejora, analice estos últimos datos
mediante una carta p.
b) ¿Las mejoras dieron resultado? Argumente.
LCS 0.061
LCC 0.027
LCI 0.0
0.070
0.060
0.050
Proporción
0.040
LCS
0.030 LCC
0.020 LCI
0.010
0.000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

99. 8. En un proceso se produce por lotes y estos se prueban al 100%. Se lleva un registro de la
proporción de artículos defectuosos por diferentes causas. Los datos de los últimos 25 lotes
se muestran a continuación:
Lote Tamaño Defectuosos Lote Tamaño Defectuosos
1 200 21 14 200 21
2 200 20 15 200 25
3 200 27 16 200 29
4 200 33 17 200 20
5 200 22 18 220 28
6 200 40 19 220 18
7 180 27 20 220 24
8 180 23 21 200 13
9 180 20 22 200 23
10 200 26 23 200 12
11 200 28 24 200 19
12 200 21
25 200 26
13 200 23
Total 5,000 589
a) Obtenga una carta p usando el tamaño de subgrupo (lote) promedio.

100. b) ¿Cómo explicaría los límites de control que obtuvo a alguien que no tienen conocimientos
profundos de estadística?
c) Obtenga una carta p con límites de control variables.
d) Suponiendo que todos los lotes tienen el mismo tamaño (el promedio), obtenga una carta
np para tales datos.
e) ¿Observa alguna diferencia importante entra la carta p y la np?
f) ¿De qué depende la elección entre la carta p o np?
P-promedio 0.117
LCS 0.184
LCI 0.049
LCC 0.117
Carta p
0.250
0.200
0.150 Proporcion
LCS
0.100 LCI
LCC
0.050
0.000
1 3 5 7 9 11 13 15 17 19 21 23

101. Carta p (Límites Variables)
Carta np
n 200
p 0.117
np 23.458
LCS 37.110
LCC 23.458
LCI 9.807
45
40
35
30
Defectos
25
LCS
20
LCC
15 LCI
10
5
0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

102. 9. En una fábrica de artículos de plástico inyectado se tiene el problema de la rebaba en las
piezas, que es necesario eliminarla con el retrabajo. Con el propósito de evaluar la realidad
actual y detectar posibles causas especiales de variación se decide implementar una carta de
control para el producto que más se fabrica, los datos obtenidos en 24 lotes de tamaño 500,
en cuanto a la cantidad de piezas con rebaba se muestran a continuación.
Lote Piezas defectuosas Lote Piezas defectuosas
1 86 13 98
2 95 14 126
3 113 15 9

103. 4 93 16 124
5 88 17 129
6 101 18 115
7 90 19 95
8 85 20 78
9 111 21 97
10 80 22 110
11 96 23 108
12 89 24 118
a) Calcule los límites de control para una carta p e interprételos.
b) Grafique la carta p y analícela.
c) Obtenga una carta np e interprétela.
d) ¿A su juicio cuál de las dos cartas es más conveniente es este caso? Argumente.
e) ¿El proceso es estable?
f) ¿Se puede considerar que el proceso genera buena calidad?
N 500
P 20.18%
LSC 25.56%
LIC 14.79%
0.3
0.25
0.2
Proporción
0.15 LCS
LCI
0.1 LCC
0.05
0
1 3 5 7 9 11 13 15 17 19 21 23

104. Carta np
10. En una empresa se registra el número de quejas por mal servicio. Los datos de las últimas
25 semanas se muestran enseguida.
Semana Número de quejas Semana Número de quejas
1 6 14 4
2 2 15 5
3 3 16 6

105. 4 4 17 7
5 5 18 8
6 6 19 9
7 7 20 0
8 8 21 1
9 9 22 2
10 0 23 3
11 1 24 4
12 2 25 5
13 3
a) ¿Es adecuado analizar éstos mediante una carta p? Argumente.
b) Calcule los límites de control para una carta c e interprete los límites obtenidos.
c) Obtenga la carta c y analícela.
d) ¿El proceso es estable?
e) ¿El nivel de calidad se puede considerar satisfactorio?
Subgrupo 25
c 4.4
LCS 10.69
LC 4.4
LCI -1.89
12
10
8
quejas
6
LCS
4
LCI
2
LC
0
-2 1 3 5 7 9 11 13 15 17 19 21 23 25
-4

106. 11. En una línea de ensamble o montaje de pequeñas piezas en tarjetas electrónicas se
cuantifica el número de defectos de diferente tipo por muestra de 10 tarjetas. Los defectos
encontrados en las últimas 30 muestras se listan a continuación.
Muestra Defectos Muestra Defectos
1 28 16 24
2 22 17 6
3 25 18 20
4 21 19 25
5 26 20 29
6 22 21 26
7 36 22 24

107. 8 22 23 32
9 32 24 31
10 22 25 29
11 23 26 24
12 27 27 27
13 26 28 21
14 18 29 27
15 29 30 31
31 20
32 22
33 28
34 26
35 24
a) Nótese que en promedio hay más de un defecto por tarjeta, ¿es adecuado analizar estos
datos mediante una carta p? Argumente.
b) Calcule los límites de control para una carta c e interprete los límites obtenidos.
c) Obtenga la carta c y analícela.
d) El dato de la muestra 17 es especial, por lo que habría que buscar las posibles causas que
ocasionaron esto, ¿por qué?
e) ¿Qué opina de la estabilidad del proceso?
f) ¿El nivel de calidad se puede considerar satisfactorio?
g) ¿Cómo aplicaría un análisis Pareto para enfocar mejor un proyecto de mejora?
n 10
u 2.5
LCS 4
LCI 1
LCC 2.5

108. 4.5
4
3.5
3
Defecto /Tarjeta (U)
2.5
LCS
2
LCI
1.5
LCC
1
0.5
0
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35

109. 12. En un hotel se ha llevado el registro de quejas de los clientes desde hace 15 semanas con el
número de clientes por semana, los datos se muestran en la siguiente tabla.
Promedio de defectos por
Semana Clientes Quejas
unidad
1 114 11 0.096
2 153 15 0.098
3 115 5 0.043
4 174 14 0.080
5 157 16 0.102
6 219 11 0.050
7 149 10 0.067
8 147 9 0.061
9 131 10 0.076
10 91 10 0.110
11 112 10 0.089
12 158 11 0.070
13 244 30 0.123
14 111 11 0.099
15 120 11 0.092
Total 2,195 184
a) Calcule los límites de control para una carta u para el número de quejas por cliente e
interprete los límites de obtenga.
b) Grafique la carta u correspondiente y analícela.
c) ¿La estabilidad del proceso es aceptable?
d) ¿Considera que la calidad del hotel es buena? Explique.
LCS 0.1556
LCI 0.0120
LCC 0.0838
U promedio 0.0838

110. n 146.33
Subgrupos 15
35
30
25 Quejas
20
LCS
15
LCI
10
LCC
5
0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

111. 13. Con el propósito de analizar la posibilidad de eliminar los estándares de trabajo en un
sector de una fábrica, se decide analizar el número de cierto tipo de operaciones que
realiza cada trabajador por día y semana. a continuación se muestran los resultados
obtenidos en una semana para 14 trabajadores (cada dato corresponde a un trabajador).
295 306 292 297 294 343 285 240 329 305 277 260 337 320
a) Calcule los límites de control para una carta c para el número de operaciones por
trabajador e interprete los límites que obtenga.
b) Investigue mediante la carta c correspondiente si algún trabajador está fuera del sistema.
c) En caso de estarlo, ¿qué recomendaría que se haga con tal trabajador?
Subgrupo 14
c-promedio 292.1
LCS= 343.4
LCI= 240.9
LCC= 292.1
400
350
300
250 C
200 LCS
LCI
150
LC
100
50
0
1 2 3 4 5 6 7 8 9 10 11 12 13 14

113. Bibliografía
 Control Estadístico de la Calidad y Seis Sigma
Humberto Gutiérrez Pulido y Román de la Vara Salazar
McGraw-Hill, México D.F. 2004