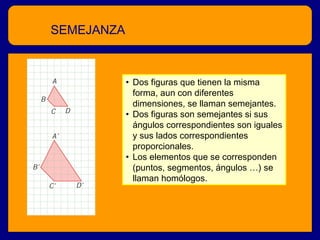
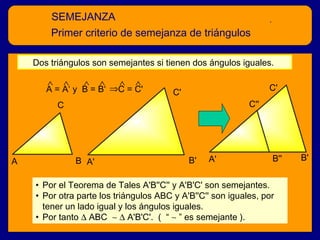
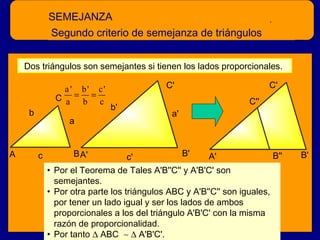
El documento describe el teorema de Tales y la semejanza de figuras geométricas. Explica que dos figuras son semejantes si tienen la misma forma pero diferentes dimensiones, y que sus ángulos correspondientes son iguales y sus lados correspondientes son proporcionales. También presenta varios criterios para determinar si dos triángulos son semejantes, como tener dos ángulos iguales, lados proporcionales, o dos lados proporcionales y un ángulo igual. Finalmente, incluye ejemplos de problemas geométricos que involuc

2. Teorema de Thales
Lados homólogos
B
A
B
AB DE
=
BC EF
AC DF
=
AB DE
D
E
C
F
A
α
F
D
β
α
β
C
E
AB es homólogo de ED
BC es homólogo de DF
AC es homólogo de EF
CASOS DE SEMEJANZA
Dos ángulos congruentes
B
F
D
A
α
β
C
β
α
E
Un ángulo congruente y los
lados que lo forman son
proporcionales
Sus tres lados proporcionales
AB AC
=
DE DF
EJERCICIOS DE REFORZAMIENTO
Problemas de Contexto
AB BC AC
=
=
DE EF DF

3. SEMEJANZA
• Dos figuras que tienen la misma
forma, aun con diferentes
dimensiones, se llaman semejantes.
• Dos figuras son semejantes si sus
ángulos correspondientes son iguales
y sus lados correspondientes
proporcionales.
• Los elementos que se corresponden
(puntos, segmentos, ángulos …) se
llaman homólogos.

4. SEMEJANZA
Figuras semejantes: Planos
Dos figuras del plano son
semejantes si los
cocientes de los
segmentos determinados
por pares cualesquiera
de puntos
correspondientes son
iguales.
es la razón de semejanza

5. SEMEJANZA
Teorema de Tales
Toda recta paralela a un lado de un triángulo, que corta a los otros
dos lados, determina un triángulo semejante al grande.
Los triángulos ABC y AB'C' son semejantes

6. SEMEJANZA
Semejanza de triángulos
.
Dos triángulos son semejantes si tienen los lados proporcionales y
los ángulos iguales.
a b c
= = =k
El cociente
a ' b' c'
se llama razón de semejanza.

7. SEMEJANZA
Primer criterio de semejanza de triángulos
.
Dos triángulos son semejantes si tienen dos ángulos iguales.
∧ ∧
∧ ∧
∧ ∧
A = A‘ y B = B‘ ⇒C = C'
 
 
 
C
A
B A'
C'
C'
C''
B'
A'
B''
• Por el Teorema de Tales A'B''C'' y A'B'C' son semejantes.
• Por otra parte los triángulos ABC y A'B''C'' son iguales, por
tener un lado igual y los ángulos iguales.
• Por tanto ∆ ABC ∼ ∆ A'B'C'. ( “ ∼ ” es semejante ).
B'

8. SEMEJANZA
Segundo criterio de semejanza de triángulos
.
Dos triángulos son semejantes si tienen los lados proporcionales.
a ' b' c'
C a = b = c
b
A
a
c
C'
C'
b'
C''
a'
B'
B''
A'
c'
• Por el Teorema de Tales A'B''C'' y A'B'C' son
semejantes.
• Por otra parte los triángulos ABC y A'B''C'' son iguales,
por tener un lado igual y ser los lados de ambos
proporcionales a los del triángulo A'B'C' con la misma
razón de proporcionalidad.
• Por tanto ∆ ABC ∼ ∆ A'B'C'.
B A'
B'

9. SEMEJANZA
6.3 – Tercer criterio de semejanza de triángulos
Dos triángulos son semejantes si tienen dos lados proporcionales y
el ángulo comprendido igual.
b'
c' ∧ ∧
= y = A A'
b
c
C
b
A
a
C'
C'
b'
C''
a'
B' A'
B''
c
c'
• Por el Teorema de Tales A'B''C'' y A'B'C' son
semejantes.
• Por otra parte los triángulos ABC y A'B''C'' son iguales,
por tener dos lados proporcionales con la misma razón
de proporcionalidad y el ángulo comprendido igual.
• Por tanto ∆ ABC ∼ ∆ A'B'C'.
c
B A'
B'

10. SEMEJANZA: PROBLEMAS

11. 5. Problema del contexto:
Calcular BC, si AB =BC, BE=6, ED=4
Los triángulos ABE y ABD son
semejantes:
B
B
6
B
2α+2β
2β
6
α+β
β
α+β
E
A
x
x
β
A
x
≈
x
α
α+β
A
E
2α 4
α+β
C
β
D
x 6
=
10 x
x 2 = 60
(2α+2β−2α)/2=m<ADB
x = 60
2β/2=m<ADB
x = 4.15
β=m<ADB
x = 2 15
Rpta: 2 raíz cuadrada de 15
10
β
D

12. 6. Problema de contexto:
Una fotografía tiene por dimensiones 15cm y 9cm. En una fotocopiadora se
hace una copia de área 170,5cm2. Determinar las dimensiones de la nueva
fotografía.
Solución:
15cm
9cm
Entonces:
15k.9k=170,5 (Área de la
copia)
135k2=170,5
Por lo tanto las dimensiones de
la copia de la fotografía serán:
15k=15(1,1238)= 16,857 cm.
9k= 9(1,12389=10,1142 cm.
K2=170,5/135
K2= 1,2629
K=1,1238 (aproximadamente)
Respuesta: La copia tiene las dimensiones de 16,857 y 10,1142
aproximadamente.

13. 7. Un terreno tiene la forma de un triángulo isósceles, cuya base mide 20m y la
altura 30m. Determina su perímetro del triángulo que se obtiene al unir los
puntos medios de sus lados.
Si M,N,P son puntos medio y los
segmentos MN, NP, MP, son
segmentos que unen los puntos
medio, entonces, estas son
paralelas a sus lados opuestos y
A
a
M
a
30
N
a
a
10
P
20
10
10+5 10 + 5 10 =Perímetro
10 + 10 10
=Perímetro
10(1 + 10 )
=Perímetro
Por ejemplo: MN=20/2
El triángulo APB es rectángulo, donde :
A
C
MN+NP+PM=Perímetro
Por pitágoras:
B
302+102=(2a)2
30
P
900+100=4a2
10
B
1000=a2
4
a2=250
a = 250
a = 5 10
Respuesta: El perímetro del triángulo que se obtiene al unir los puntos medios es 10(1 + 10 ) m.