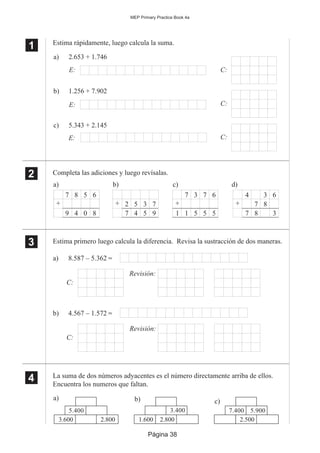
El documento presenta varios ejercicios de matemáticas que involucran números decimales. En la primera sección, se piden escribir números dados en tabla de valor posicional y describirlos con palabras. Luego, se piden aproximar números a decenas, centenas y unidades de mil; ordenar números de forma ascendente y descendente; y realizar cálculos como sumas, restas, multiplicaciones y divisiones con números decimales. Finalmente, se presentan ejercicios adicionales de adición y sustracción con valores posicionales.