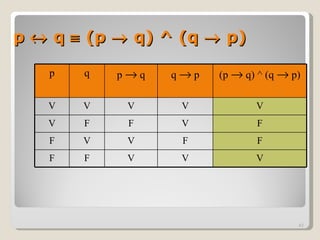
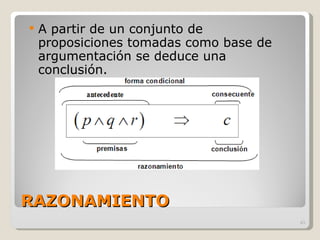
El documento presenta una introducción a la lógica, definiendo conceptos como proposición, premisa, conclusión, inferencia, implicación y falacia. Explica que la lógica estudia los razonamientos sin tomar en cuenta su contenido, buscando determinar si las conclusiones se derivan válidamente de las premisas. También introduce conceptos de lógica formal como tablas de verdad, proposiciones atómicas y moleculares, y conectivos lógicos como la negación, conjunción y disyunción.

1. LÓGICA

17. CONECTIVOS LÓGICOS

33. EJEMPLO: p q p v q p v q V V V F V F V F F V V F F F F V p q p q p ^ q V V F F F V F F V F F V V F F F F V V V

38. TABLA DE VERDAD DEL CONDICIONAL La implicación de p a q es falsa únicamente en el caso de que el antecedente p sea verdadero y que el consecuente q sea falso p q p  q V V V F V V V F F F F V

42. p  q  (p  q) ^ (q  p) p q p  q q  p (p  q) ^ (q  p) V V V V V V F F V F F V V F F F F V V V

44. TABLA DE VERDAD DE ( (p  q) ^ p )  q La tabla indica que el razonamiento es correcto independientemente de las proposiciones utilizadas p q p  q (p  q) ^ p ( (p  q) ^ p )  q V V V V V V F F F V F V V F V F F V F V