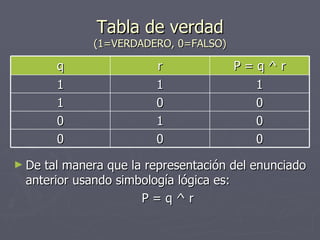
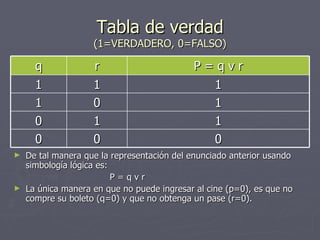
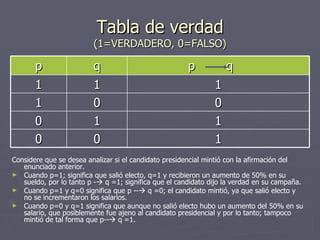
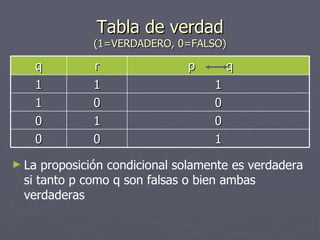
Este documento resume conceptos básicos de lógica matemática como proposiciones, operadores lógicos, tablas de verdad y clasificación de proposiciones. Define proposiciones simples y compuestas, y explica los operadores de negación, conjunción, disyunción, condicionales y bicondicionales. Además, introduce el uso de tablas de verdad para determinar el valor de verdad de proposiciones compuestas.

1. LÓGICA MATEMÁTICA Estudia las frases, afirmaciones y el comportamiento de ambas. En el estudio de conjuntos intervienen frases y expresiones.

2. Proposición Expresión verdadera o falsa pero no ambas Ejemplos: 3 + 8 es menor que 10 Amado Nervo fue un gran arquitecto El petróleo es un recurso renovable

3. No son proposiciones: Es más interesante Oceanía que América Es más fácil el estudio de la música que de las matemáticas. La cosecha del año entrante se helará

4. Denotación Proposiciones: Letras minúsculas Proposiciones falsas: F (valor de verdad falso) Proposiciones verdaderas: V (valor de verdad verdadero)

5. Clasifica las proposiciones 3 + 8 es menor que 10 (_F__) Amado Nervo fue un gran arquitecto(__F_) El petróleo es un recurso renovable(__F_) Es más interesante Oceanía que América(_X_) Es más fácil el estudio de la música que de las matemáticas. (__X_) La cosecha del año entrante se helará(__X_)

6. Clasificación Proposición simple Proposición compuesta Proposición Disyuntiva Proposición Conjuntiva

7. Proposiciones compuestas Formadas por varias proposiciones y usa operadores o conectores: Y ( ^) conjunción O (v) disyunción No (¬, ´) Entonces ( ) Condicionales Si sólo si ( ) Bicondicionales

8. Conjunción Y ( ^) Se utiliza para conectar dos proposiciones que se deben cumplir para que se pueda obtener un resultado verdadero. Se le conoce como la multiplicación lógica. Ejemplo: “El coche enciende cuando tiene gasolina en el tanque y tiene corriente la batería” Sean: P = El coche enciende q = Tiene gasolina el tanque r = Tiene corriente la batería

9. Tabla de verdad (1=VERDADERO, 0=FALSO) De tal manera que la representación del enunciado anterior usando simbología lógica es: P = q ^ r q r P = q ^ r 1 1 1 1 0 0 0 1 0 0 0 0

10. Disyunción “O” , “u” (v) Se obtiene un resultado verdadero cuando alguna de las proposiciones es verdadera. Se conoce como la suma lógica. Ejemplo: “Una persona puede entrar al cine si compra su boleto u obtiene un pase” P = Entra al cine q = Compra su boleto r = Obtiene un pase

11. Tabla de verdad (1=VERDADERO, 0=FALSO) De tal manera que la representación del enunciado anterior usando simbología lógica es: P = q v r La única manera en que no puede ingresar al cine (p=0), es que no compre su boleto (q=0) y que no obtenga un pase (r=0). q r P = q v r 1 1 1 1 0 1 0 1 1 0 0 0

12. Negación No (¬, ´) Su función es negar la proposición. Esto significa que sí alguna proposición es verdadera y se le aplica el operador no se obtendrá su complemento o negación (falso). Ejemplo: La negación de está lloviendo en este momento (p=1), es no está lloviendo en este momento (p’=0)

13. Tabla de verdad (1=VERDADERO, 0=FALSO) p P´ 1 0 0 1

14. Ejemplo Sean las proposiciones: p: Hoy es domingo. q: Tengo que estudiar teorías del aprendizaje. r: Aprobaré el curso. El enunciado: “Hoy es domingo y tengo que estudiar teorías de aprendizaje o no aprobaré el curso”. Se puede representar simbólicamente de la siguiente manera: p ^ q v´ r

15. Entonces ( ) Condicionales Es aquella que está formada por dos proposiciones simples (o compuesta) p y q. La cual se indica de la siguiente manera: P q Se lee “Si p entonces q”

16. Ejemplo. El candidato del PRI dice “Si salgo electo presidente de la República recibirán un 50% de aumento en su sueldo el próximo año”. Una declaración como esta se conoce como condicional. Sean: p: Salió electo Presidente de la República. q: Recibirán un 50% de aumento en su sueldo el próximo año. El enunciado se puede expresar de las siguiente manera. p q

17. Tabla de verdad (1=VERDADERO, 0=FALSO) Considere que se desea analizar si el candidato presidencial mintió con la afirmación del enunciado anterior. Cuando p=1; significa que salió electo, q=1 y recibieron un aumento de 50% en su sueldo, por lo tanto p -  q =1; significa que el candidato dijo la verdad en su campaña. Cuando p=1 y q=0 significa que p --  q =0; el candidato mintió, ya que salió electo y no se incrementaron los salarios. Cuando p=0 y q=1 significa que aunque no salió electo hubo un aumento del 50% en su salario, que posiblemente fue ajeno al candidato presidencial y por lo tanto; tampoco mintió de tal forma que p--  q =1. p q p q 1 1 1 1 0 0 0 1 1 0 0 1

18. Bicondicional Sean p y q dos proposiciones entonces se puede indicar la proposición bicondicinal de la siguiente manera: p q Se lee “p si y solo si q” Esto significa que p es verdadera si y solo si q es también verdadera. O bien p es falsa si y solo si q también lo es.

19. Ejemplo El enunciado siguiente es una proposición bicondicional “ Es buen estudiante, si y solo si; tiene promedio de diez” Donde: p: Es buen estudiante. q: Tiene promedio de diez.

20. Tabla de verdad (1=VERDADERO, 0=FALSO) La proposición condicional solamente es verdadera si tanto p como q son falsas o bien ambas verdaderas q r p q 1 1 1 1 0 0 0 1 0 0 0 1

21. Ejercicio Sea el siguiente enunciado: “ Si no pago la luz, entonces me cortarán la corriente eléctrica. Y Si pago la luz, entonces me quedaré sin dinero o pediré prestado. Y Si me quedo sin dinero y pido prestado, entonces no podré pagar la deuda, si solo si soy desorganizado”

22. Donde: p: Pago la luz. q: Me cortarán la corriente eléctrica. r: Me quedaré sin dinero. s: Pediré prestado. t: Pagar la deuda. w: soy desorganizado.

23. Tablas de verdad Representación de las hipótesis generalizadas mediante proposiciones compuestas. Sirve para determinar el valor de verdad de cada componente de una proposición que contiene conectivos. Establecen una correspondencia mediante la deducción lógico matemática. Constituye un método de decisión para establecer si una proposición es o no un teorema.

24. Construcción: 1 = VERDADERO 0 = FALSO Tabla de verdad

25. Tabla de verdad El número de líneas de la tabla de verdad depende del número de variables de la expresión y se puede calcular por medio de la siguiente formula: No de líneas = 2n Donde: n = número de variables distintas.

26. NEGACIÓN Dada una proposición p , se define la negación de p como la proposición p' (~, ¬) que es verdadera cuando p es falsa y que es falsa cuando p es verdadera. Se lee "no p ".

27. Conjunción Es aquella proposición que es verdadera cuando p y q son verdaderas, y falsa en cualquier otro caso. Se escribe p ̭ q, y se lee "p y q".

28. Disyunción Es aquella proposición que es verdadera cuando al menos una de las dos p o q es verdadera, falsa en caso contrario. Se escribe p ̮̮ q, y se lee "p ó q".

29. Disyunción exclusiva Es aquella proposición que es verdadera cuando una y sólo una de las dos p o q es verdadera, y falsa en cualquier otro caso. Se escribe p q, y se lee "p o q pero no ambas". Se usa muy poco.

30. Condicional E s aquella proposición que es falsa únicamente cuando la condición suficiente p es verdadera y la condición necesaria q es falsa. Se escribe p => q, y se lee "si p entonces q".

31. Bicondicional Es aquella proposición que es verdadera cuando p y q tienen el mismo valor de verdad, y falsa en caso contrario. Se escribe p <=>q, y se lee &quot;si y sólo si p entonces q&quot;.

32. Tautología Se dice que una proposición es una tautología si su valor de verdad es siempre 1 independientemente de los valores de las proposiciones que lo componen; por ejemplo:

33. Contradicción Una proposición se dice que es una contradicción si su valor de verdad es siempre 0 independientemente de los valores de las proposiciones que lo componen. Por ejemplo:

34. Paradoja Una paradoja es una proposición a la que no se le puede asignar ningún valor de verdad; suelen estar relacionadas con incorrecciones en el lenguaje lógico. Por ejemplo: p = &quot;la proposición p es falsa&quot;.

35. Equivalentes Dos proposiciones p y q se dicen equivalentes si tienen la misma tabla de verdad en función de las proposiciones elementales que lo componen; esta definición equivale a decir que la proposición es una tautología. Por ejemplo, las proposiciones: son equivalentes.

36. Reducción al absurdo Esta ley se llama &quot;ley del contrarrecíproco&quot;, y se usa en los razonamientos por reducción al absurdo .