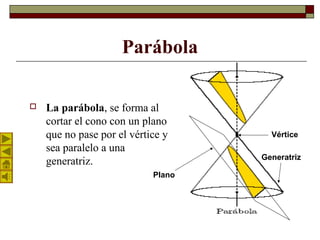
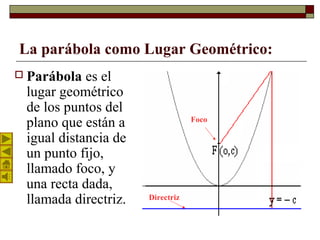
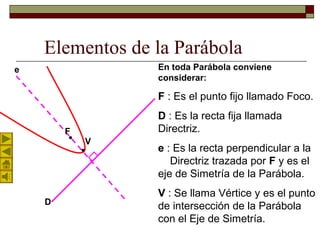
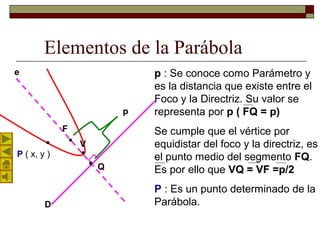
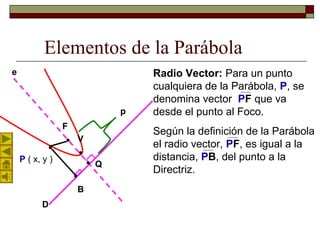
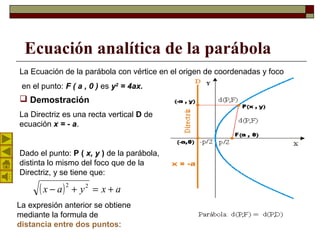
Este documento describe la parábola geométrica. Explica que una parábola es el lugar geométrico de puntos equidistantes de un punto fijo llamado foco y una recta llamada directriz. Detalla los elementos clave de una parábola como el vértice, foco, directriz y parámetro. Además, presenta la ecuación analítica de una parábola general y un ejemplo numérico. Por último, explica la propiedad de reflexión de una parábola parabólica que hace que la luz incidente paral

1. Parábola

2. Índice
 La parábola.
 La parábola como lugar geométrico.
 Elementos de la parábola.
 Ecuación analítica de la parábola.
 Ejemplo.
 Propiedades de reflexión de la parábola.

3. Parábola
 La parábola, se forma al
cortar el cono con un plano
que no pase por el vértice y
sea paralelo a una
generatriz.
Vértice
Plano
Generatriz

4. La parábola como Lugar Geométrico:
 Parábola es el
lugar geométrico
de los puntos del
plano que están a
igual distancia de
un punto fijo,
llamado foco, y
una recta dada,
llamada directriz.
Foco
Directriz

5. Elementos de la Parábola
F
D
V
e En toda Parábola conviene
considerar:
F : Es el punto fijo llamado Foco.
D : Es la recta fija llamada
Directriz.
e : Es la recta perpendicular a la
Directriz trazada por F y es el
eje de Simetría de la Parábola.
V : Se llama Vértice y es el punto
de intersección de la Parábola
con el Eje de Simetría.

6. Elementos de la Parábola
F
D
V
Q
P ( x, y )
p : Se conoce como Parámetro y
es la distancia que existe entre el
Foco y la Directriz. Su valor se
representa por p ( FQ = p)
Se cumple que el vértice por
equidistar del foco y la directriz, es
el punto medio del segmento FQ.
Es por ello que VQ = VF =p/2
P : Es un punto determinado de la
Parábola.
p
e

7. Elementos de la Parábola
F
D
V
Q
P ( x, y )
Radio Vector: Para un punto
cualquiera de la Parábola, P, se
denomina vector PF que va
desde el punto al Foco.
Según la definición de la Parábola
el radio vector, PF, es igual a la
distancia, PB, del punto a la
Directriz.
p
B
e

8. Ecuación analítica de la parábola
La Ecuación de la parábola con vértice en el origen de coordenadas y foco
en el punto: F ( a , 0 ) es y2
= 4ax.
 Demostración
La Directriz es una recta vertical D de
ecuación x = - a.
Dado el punto: P ( x, y ) de la parábola,
distinta lo mismo del foco que de la
Directriz, y se tiene que:
( ) axyax +=+− 22
La expresión anterior se obtiene
mediante la formula de
distancia entre dos puntos:

9. Después en esta ecuación se elevan al cuadrado los binomios y se agrupan
términos
( ) ( )2
2
22
axyax +=



 +−
( ) ( )222
axyax +=+−
22222
22 aaxxyaaxx ++=++−
axy 42
=
Como a > 0, puede tomar cualquier valor positivo.
El eje de simetría de la parábola es el eje x positivo.
La parábola es simétrica con respecto a su eje, pues y =± 2 ax

10. axy 42
=
Lado
Recto
La cuerda trazada por el foco y
perpendicular al eje de la parábola se le da
el nombre de Lado Recto.
Se determina mediante las coordenadas de
sus extremos. Sustituyendo a con x en la
ecuación y2
= 4ax, se encuentra:
y2
= 4a2
y y = ±2a
Los extremos son (a, -2a) y (a, 2a)
Y la longitud del Lado Recto es 4a
Para finalizar…

11. Generalizando… Las Ecuaciones de
la parábola con vértice en el origen
 La ecuación de una parábola con vértice en el
origen y foco en (a, 0) es y2
=4ax
La parábola se abre hacia la derecha si a>0 y se abre hacia
la izquierda si a<0.
 La ecuación de una parábola con vértice en el
origen y foco en (0, a) es x2
=4ay
La parábola se abre hacia la arriba si a>0 y se abre hacia
la abajo si a<0.

12.  Si la parábola no tiene su vértice en (0,0) si no en (h, k) entonces la ecuación sería:
1.- La ecuación de la parábola con vértice en (h, k) y foco en (h + a, k) es:
(y – k)2
= 4a(x – h)
2.- La ecuación de la parábola con vértice en (h, k) y foco en h +a, k) es:
(x – h)2
= 4a(y – k)
 Desarrollando la ecuación tendremos:
y2
+ k2
– 2yk + 4ax – 4ah = 0 ó x2
+ h2
– 2xh + 4ay – 4ak = 0
 Cuando h = 0 y k = 0, se reducen a ecuaciones más simples hacemos
y2
+ Dx + Ey + F = 0 ó x2
+ Dx + Ey + F = 0
 Siempre que E = 0 y D = 0
Ecuación analítica de la parábola con vértice en (h, k)

13. Ejemplo
 Escríbase la ecuación de la parábola con vértice en el
origen y foco en (0, 4).
Ecuación:
x2
=4ay
La distancia del vértice al foco es 4 y, por tanto, a = 4.
sustituyendo este valor con a se obtiene:
x2
=16y
Haz click para
observar la gráfica

14. Propiedad de reflexión de la parábola:
 Por ejemplo; Si se recibe luz de una
fuente lejana con un espejo parabólico, de
manera que los rayos incidentes son
paralelos al eje del espejo, entonces la luz
reflejada por el espejo se concentra en el
foco.

15. Propiedad de reflexión de la
parábola
Esto se basa en el
hecho de que,
en los espejos
planos, cóncavos
y convexos, los
rayos iguales se
reflejan en
ángulos iguales.