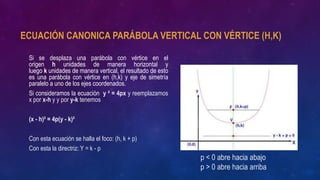
La parábola es una curva geométrica definida como el lugar de los puntos equidistantes de un foco y una directriz. Tiene elementos como el foco, directriz, eje focal, vértice y parámetro. Su ecuación canonica depende de si el eje focal es horizontal o vertical y la posición del vértice. Algunas aplicaciones son antenas parabólicas, cocinas y centrales solares, diseño de puentes y pliegues de papel.

1. LA PARÁBOLA

2. DEFINICIÓN:
La parábola es una curva abierta y plana,
que se define como el lugar geométrico
de los puntos del plano que equidistan de
un punto denominado foco, y una recta
denominada directriz, observando la
figura, FP = PQ = r.

3. El eje de la parábola es la recta perpendicular
a la directriz, que pasa por el foco F. La
distancia FD, del foco a la directriz, se
denomina parámetro de la parábola, el punto
medio del segmento FD, es el punto V, que se
denomina vértice de la parábola.

4. ELEMENTOS
• El punto F se denomina foco
• La recta l es la directriz
• La recta que contiene el foco y es perpendicular a la
directriz se llama eje focal o eje de simetría E.
• El punto de corte de la parábola con el eje se denomina
vértice V, y equidista del foco y la directriz.
• Se denomina parámetro a la distancia del foco a la
directriz y se expresa como 2p.
• La cuerda AB que pasa por el foco y es perpendicular al
eje focal se llama lado recto

5. ECUACIÓN CANONICA DE LA PARÁBOLA
Supongamos que F tiene coordenadas (0, p) y la recta d tiene
ecuación y = − p con p > 0. Observe la gráfica:
Observe que d (P,F) = (x − 0)2 + ( y − p)2 y que d (P,l) = y + p .
Igualando distancias y resolviendo:
Observe que d (P,F) = [ (x − 0)2 + ( y − p)2 ] y que d (P,l) = y + p .
Igualando distancias y resolviendo:
d(P,F) = d (P,l )
 [ (x − 0)2 + ( y − p)2 ] = y + p
( [ (x − 0)2 + ( y − p)2 ])2 = (y + p)2
x2 + y2 – 2py + p2 = y2 + 2py + p2
x2 = 4py
Observe que para la parábola anterior el eje focal es el eje y , el vértice es el
punto (0,0) y además que la parábola es cóncava hacia arriba. Se denomina
parábola vertical (eje y)
p < 0 abre hacia arriba
p > 0 abre hacia abajo

6. ECUACIÓN CANONICA PARÁBOLA HORIZONTAL (EJE
X) CON VÉRTICE (0,0)
y ² = 4px
Vértice (0,0)
Para hallar el foco:
F = (p, 0)
Para hallar la directriz:
x = - p
p < 0 abre a la izquierda
p > 0 abre a la derecha

7. ECUACIÓN CANONICA PARÁBOLA VERTICAL CON VÉRTICE (H,K)
Si se desplaza una parábola con vértice en el
origen h unidades de manera horizontal y
luego k unidades de manera vertical, el resultado de esto
es una parábola con vértice en (h,k) y eje de simetría
paralelo a uno de los ejes coordenados.
Si consideramos la ecuación y ² = 4px y reemplazamos
x por x-h y y por y-k tenemos
(x - h)² = 4p(y - k)²
Con esta ecuación se halla el foco: (h, k + p)
Con esta la directriz: Y = k - p
p < 0 abre hacia abajo
p > 0 abre hacia arriba

8. ECUACIÓN CANONICA PARÁBOLA HORIZONTAL CON VÉRTICE (H,K)
Si se desplaza una parábola con vértice en el
origen h unidades de manera horizontal y luego k unidades
de manera vertical, el resultado de esto es una parábola
con vértice en (h,k) y eje de simetría paralelo a uno de los
ejes coordenados.
Si consideramos la ecuación y ² = 4px y reemplazamos x
por x-h y y por y-k tenemos
(y - k)² = 4p(x - h)
Para hallar el foco:
F = (h +p, k)
Para hallar la directriz:
x= h - p
p < 0 abre a la izquierda
p > 0 abre a la derecha

9. APLICACIONES PRÁCTICAS
Las aplicaciones prácticas son muchas: las antenas
satelitales y radiotelescopios aprovechan el principio
concentrando señales recibidas desde un emisor
lejano en un receptor colocado en la posición del
foco.
La concentración de la radiación solar en un punto,
mediante un reflector parabólico tiene su aplicación
en pequeñas cocinas solares y grandes centrales
captadoras de energía solar.

10. EN EL DISEÑO ESTRUCTURAL Y ARQUITECTÓNICO DE
PUENTES

11. CONSTRUCCIÓN PLEGANDO PAPEL
https://www.youtube.com/watch?v=UDgMlSlDSEw