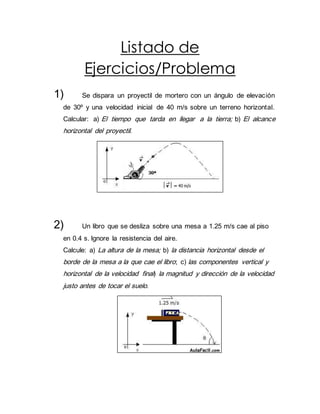
Este documento presenta la solución a 3 problemas de física que involucran movimiento parabólico. El primer problema calcula el tiempo y alcance de un proyectil disparado con ángulo de 30° y velocidad inicial de 40 m/s. El segundo analiza el movimiento de un libro deslizándose por una mesa e identifica su altura, distancia y velocidad final. El tercer problema determina el tiempo de vuelo, altura máxima y componentes de velocidad de una pelota arrojada con ángulo de 42° a una pared.

1. Listado de
Ejercicios/Problema
1) Se dispara un proyectil de mortero con un ángulo de elevación
de 30º y una velocidad inicial de 40 m/s sobre un terreno horizontal.
Calcular: a) El tiempo que tarda en llegar a la tierra; b) El alcance
horizontal del proyectil.
2) Un libro que se desliza sobre una mesa a 1.25 m/s cae al piso
en 0.4 s. Ignore la resistencia del aire.
Calcule: a) La altura de la mesa; b) la distancia horizontal desde el
borde de la mesa a la que cae el libro; c) las componentes vertical y
horizontal de la velocidad final) la magnitud y dirección de la velocidad
justo antes de tocar el suelo.

2. 3) Una persona arroja una pelota a una velocidad de 25.3 m/s y
un ángulo de 42º arriba de la horizontal directa hacia una pared como
se muestra en la figura.
La pared está a 2.18 m del punto de salida de la pelota. a) ¿Cuánto
tiempo estará la pelota en el aire antes de que golpee a la
pared?; b) ¿A qué distancia arriba del punto de salida golpea la pelota
a la pared?; c) ¿Cuáles son las componentes horizontales y verticales
de su velocidad cuando golpea a la pared?; d) ¿Ha pasado el punto
más elevado de su trayectoria cuando la golpea?
Solución de cada
Ejercicio/Problema
1.Se tiene el valor de la magnitud de la velocidad inicial y el ángulo de
elevación. A partir de ello, se pueden encontrar las componentes de
la velocidad inicial Vox y Voy:

3. Vox = Vo cos θ = (40 m/s) cos (30º) = 34.64 m/s. (Ésta es constante)
Voy = Vo Sen θ = (40 m/s) sen (30º) = 20.0 m/s.
a) Si analizamos el tiempo en el que el proyectil tarda en llegar a la
altura máxima, podemos encontrar el tiempo total del movimiento,
debido a que es un movimiento parabólico completo. Suponga que
tº es el tiempo en llegar a la altura máxima.
En el punto de la altura máxima, Vfy = 0 m/s. El valor de la
aceleración de la gravedad, para el marco de referencia en la
figura, siempre es negativo (un vector dirigido siempre hacia
abajo).
De la ecuación de caída libre:
Como tº = t/2, donde t es el tiempo total del movimiento:
t = 2 * (2.04 s) = 4.08 s
b) El tiempo total del movimiento es el mismo tiempo en el que se
obtiene el alcance horizontal. De M.R.U.:
d = Xmax = Vx * t = (34.64 m/s) * (4.08 s) = 141.33 m
2.Éste ejemplo comienza su movimiento justo a la mitad de un tiro
parabólico completo; por lo tanto, se comienza en la altura
máxima de un movimiento de proyectil, con una velocidad inicial
en y igual a cero (Voy = 0 m/s).
a) La altura de la mesa es igual a la altura máxima del
movimiento. Como la altura es el desplazamiento en el eje y,
comenzamos analizando en dicho eje.

4. De la fórmula: Vfy = Voy + g*t
se obtiene: Vfy = (0 m/s) + (-9.8 m/s^2)*(0.4 s) = - 3.92 m/s
El signo negativo indica el sentido de la velocidad final (hacia
abajo). Luego:
b) El signo negativo muestra que la altura estaba medida desde el
borde de la mesa e indica que son 0.784 m hacia abajo.
La velocidad en y al principio del tiro semiparabólico es igual a
cero, pero la velocidad no, debido a que tiene una componente
en x, que es igual a la velocidad con la que llega al borde de la
mesa y se cae de ella. La velocidad en x no cambia, entonces:
Si d es la distancia horizontal del movimiento:
d = (1.25 m/s)*(0.4 s) = 0.5 m
c) La componente de la velocidad, en x, no cambia; entonces:
Vfx = 1.25 m/s
La componente de la velocidad, en y, se calculó en el literal
a) del ejercicio:
Vfy = 3.92 m/s
d) Obtenidas las componentes, podemos encontrar la magnitud Vf
de la velocidad final:
y la dirección está dada por:
Note que la magnitud de un vector siempre es positiva.
Un vector representa su sentido por medio del signo a partir de
un marco de referencia propuesto, pero cuando es una

5. magnitud que se representa, ésta siempre tiene signo positivo.
3.Este es un movimiento parabólico general; es decir, no es
completo ni semiparabólico, pero tiene el comportamiento
parabólico característico.
a) Se conoce la distancia recorrida en x. Con la magnitud y dirección
del vector de la velocidad inicial se puede encontrar la
componente de velocidad en x. Entonces:
Vx = (25.3 m/s) cos (42º) = 18.80 m/s
El tiempo de vuelo está dado por:
b) La distancia que se pide se mide en el eje y. Analizando el
movimiento en ese eje, se puede encontrar la velocidad final, en
y, antes de golpear la pared:
Voy = (25.3 m/s) sen (42º) = 16.93 m/s
La velocidad final, en y, es:
Vfy = Voy + g*t = (16.93 m/s) + (-9.8 m/s^2)*(1.16 s) = 5.56
m/s
Note que la velocidad final en y es positiva. El sentido de ésa
componente indica que la velocidad apunta hacia arriba.
c) Las componentes verticales y horizontales de la velocidad final se
calcularon en literales anteriores:
Vfx = 18.80 m/s
Vfy = 5.56 m/s
d) El punto h se puede comparar con el punto más alto del
movimiento, tomando como Vfy = 0 m/s:
Como Ymáx > h; entonces la pelota no ha pasado su punto más

6. alto de la trayectoria parabólica. Esto se puede demostrar también
con el sentido de la velocidad, debido a que la velocidad, en y,
cuando golpea la pared, es positivo.
Esto quiere decir que la pelota estaba subiendo cuando golpea la
pared; si ésta no estuviera, la pelota siguiera una trayectoria
ascendente hasta llegar a la altura máxima.