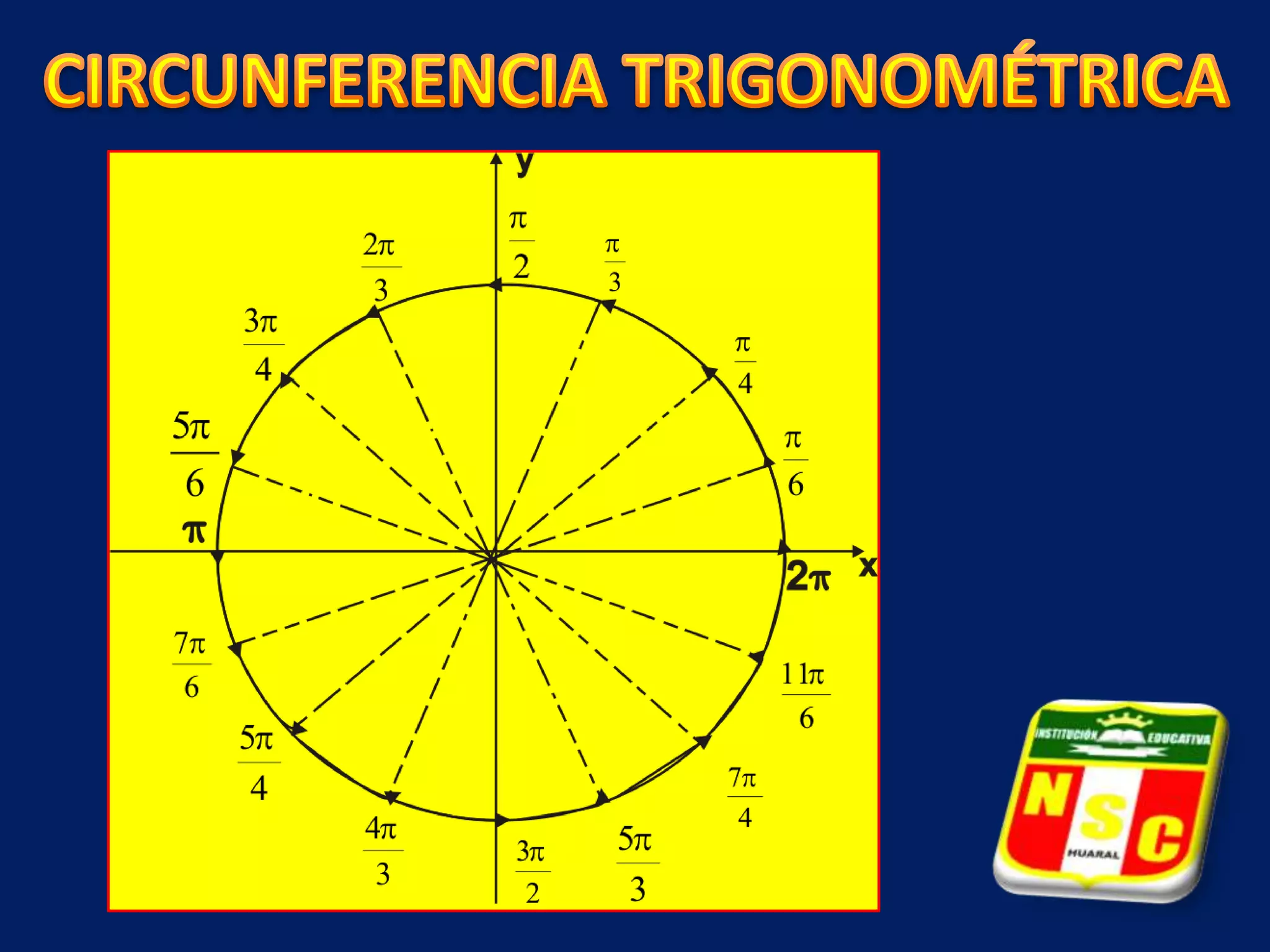
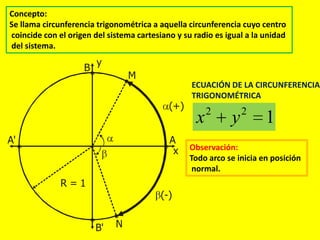
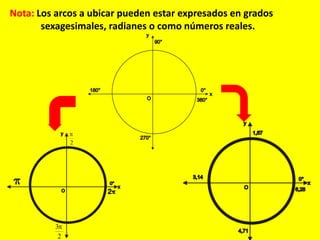
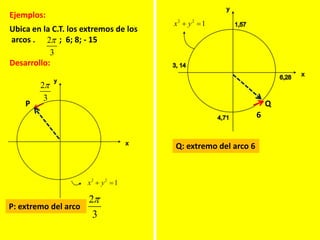
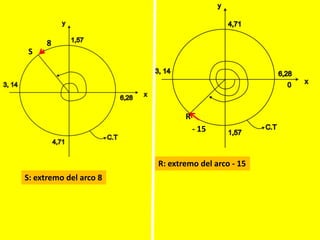
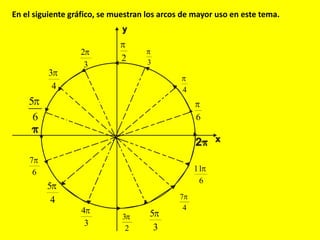
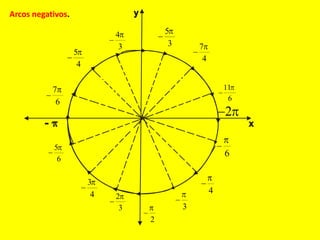
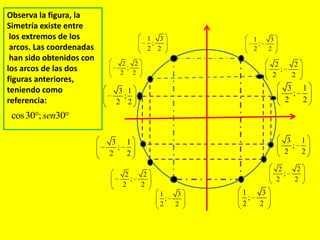
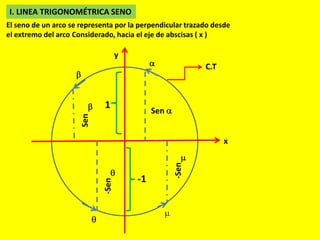
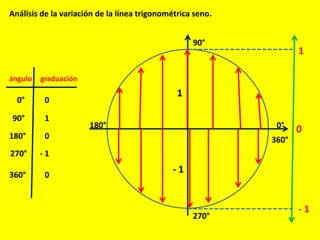
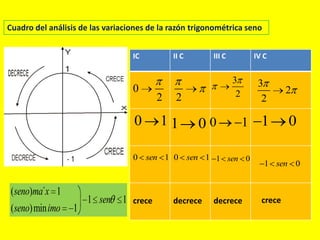
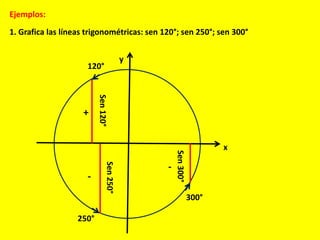
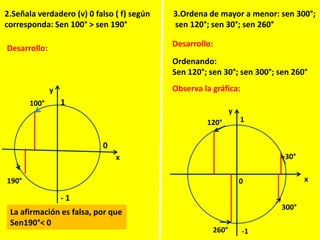
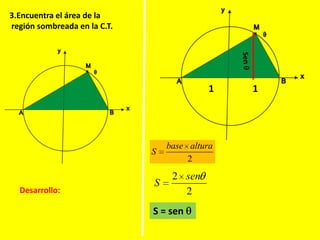
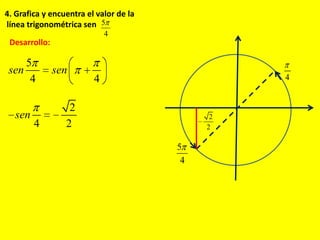
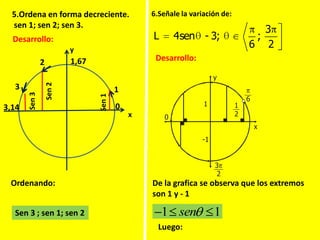
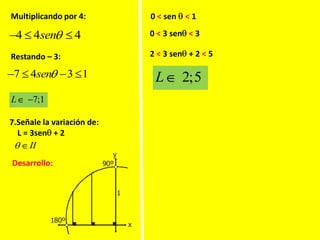
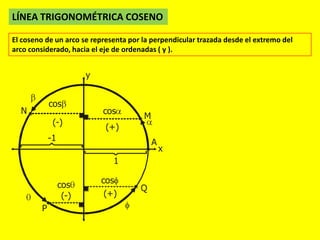
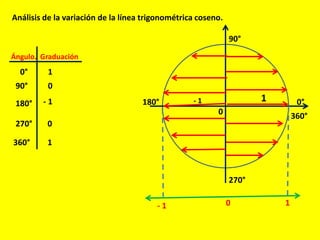
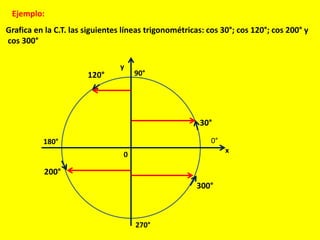
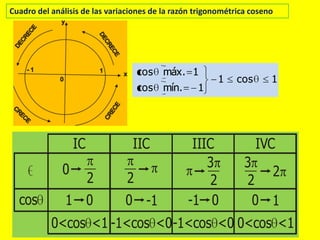
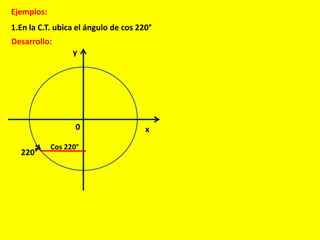
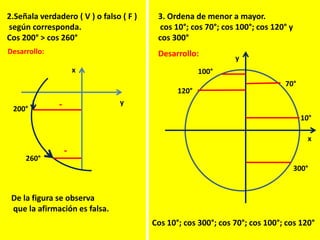
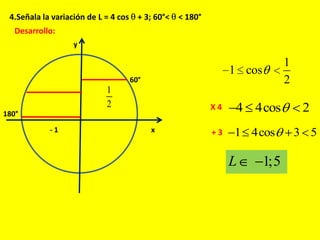
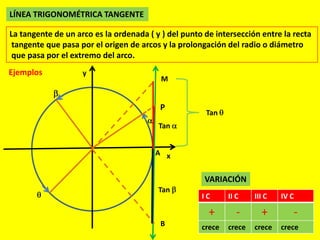
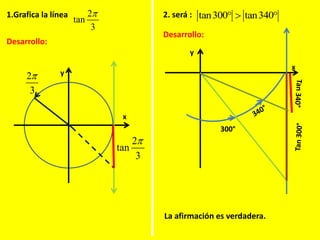
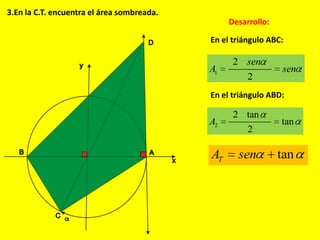
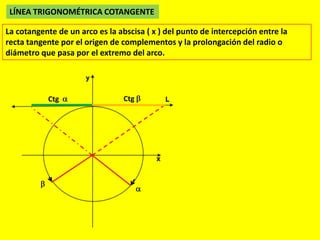
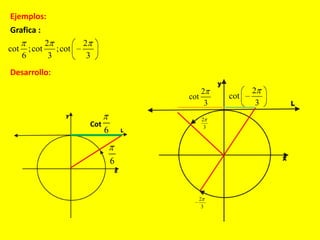
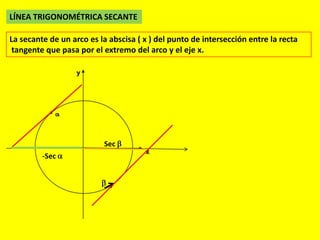
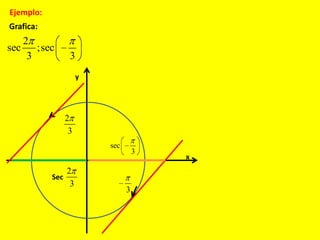
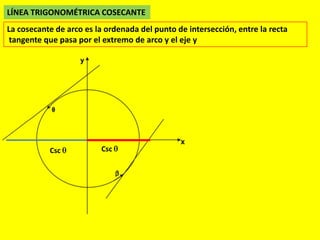
Este documento describe las líneas trigonométricas básicas (seno, coseno, tangente, cotangente, secante y cosecante) y su variación en la circunferencia trigonométrica. Explica que la circunferencia trigonométrica tiene un radio de 1 unidad y su centro coincide con el origen del sistema cartesiano. Además, incluye ejemplos de cómo graficar estas líneas trigonométricas y ordenar o comparar sus valores para diferentes ángulos.

2. Concepto:
Se llama circunferencia trigonométrica a aquella circunferencia cuyo centro
coincide con el origen del sistema cartesiano y su radio es igual a la unidad
del sistema.
B
y
M
B' N
R = 1
A' A
x
(+)
(-)
ECUACIÓN DE LA CIRCUNFERENCIA
TRIGONOMÉTRICA
2 2
1x y
Observación:
Todo arco se inicia en posición
normal.

3. Nota: Los arcos a ubicar pueden estar expresados en grados
sexagesimales, radianes o como números reales.

4. Ejemplos:
Ubica en la C.T. los extremos de los
arcos . ; 6; 8; - 152
3
Desarrollo:
2
3
P
P: extremo del arco
2
3
Q
Q: extremo del arco 6
6

5. S
8
S: extremo del arco 8
R
- 15
R: extremo del arco - 15

6. En el siguiente gráfico, se muestran los arcos de mayor uso en este tema.

7. Arcos negativos.

8. 1 3
;
2 2
2 2
;
2 2
3 1
;
2 2
Observa la figura, la
Simetría existe entre
los extremos de los
arcos. Las coordenadas
han sido obtenidos con
los arcos de las dos
figuras anteriores,
teniendo como
referencia:
cos30 ; 30sen
1 3
;
2 2
2 2
;
2 2
3 1
;
2 2
3 1
;
2 2
2 2
;
2 2
1 3
;
2 2
1 3
;
2 2
2 2
;
2 2
3 1
;
2 2

9. I. LINEA TRIGONOMÉTRICA SENO
El seno de un arco se representa por la perpendicular trazado desde
el extremo del arco Considerado, hacia el eje de abscisas ( x )
C.T
1
-1
y
x
Sen
Sen
-Sen
-Sen

10. ángulo graduación
Análisis de la variación de la línea trigonométrica seno.
0°
90°
270°
180°
360°
0°
90°
180°
270°
360°
0
1
0
- 1
0
1
- 1
0
1
- 1

11. ( ) ´ 1
1 1
( )min 1
seno ma x
sen
seno imo
IC II C III C IV C
crece decrece decrece
2
1 0
3
20
2
0 1
0 1sen 0 1sen 1 0sen
3
2
2
1 00 1
1 0sen
crece
Cuadro del análisis de las variaciones de la razón trigonométrica seno

12. Ejemplos:
1. Grafica las líneas trigonométricas: sen 120°; sen 250°; sen 300°
y
x
120°
250°
300°
Sen120°
Sen250°
Sen300°
+
-
-

13. 2.Señala verdadero (v) 0 falso ( f) según
corresponda: Sen 100° > sen 190°
1
0
- 1
x
y
100°
190°
Desarrollo:
La afirmación es falsa, por que
Sen190°< 0
3.Ordena de mayor a menor: sen 300°;
sen 120°; sen 30°; sen 260°
Desarrollo:
Ordenando:
Sen 120°; sen 30°; sen 300°; sen 260°
Observa la gráfica:
1
-1
x
y
30°
120°
260°
300°
0

14. 3.Encuentra el área de la
región sombreada en la C.T.
Desarrollo:
1 1
2
base altura
S
2
2
sen
S
S = sen

15. 4. Grafica y encuentra el valor de la
línea trigonométrica sen 5
4
Desarrollo:
5
4 4
sen sen
2
4 2
sen
5
4
4
2
2

16. 5.Ordena en forma decreciente.
sen 1; sen 2; sen 3.
Desarrollo:
x
y
1,67
3,14 0
1
2
3
Sen1
Sen2
Sen3
Ordenando:
Sen 3 ; sen 1; sen 2
6.Señale la variación de:
2
3
;
6
3;-sen4L
Desarrollo:
y
x
3
2
-1
1
0
6
1
2
De la grafica se observa que los extremos
son 1 y - 1
1 1sen
Luego:

17. 4 4 4sen
Multiplicando por 4:
Restando – 3:
7 4 3 1sen
7;1L
7.Señale la variación de:
L = 3sen + 2
II
Desarrollo:
1
x
180º
y
90º
0 < sen < 1
0 < 3 sen < 3
2 < 3 sen + 2 < 5
2;5L

18. LÍNEA TRIGONOMÉTRICA COSENO
El coseno de un arco se representa por la perpendicular trazada desde el extremo del
arco considerado, hacia el eje de ordenadas ( y ).
y
x
N
M
cos
(-)
-1
1
cos
(+)
A
P
cos
(-)
cos
(+)
Q

19. Análisis de la variación de la línea trigonométrica coseno.
Ángulo. Graduación
90°
0°180°
270°
360°0
0°
90°
180°
270°
360°
1
0
- 1
0
1
1- 1
- 1 10

20. Ejemplo:
Grafica en la C.T. las siguientes líneas trigonométricas: cos 30°; cos 120°; cos 200° y
cos 300°
y
x
0°
90°
270°
180°
0
30°
120°
200°
300°

21. Cuadro del análisis de las variaciones de la razón trigonométrica coseno
1cos1
1.míncos
1.máxcos
IC
0
2
IIC
2
IIIC
3
2
IVC
2
3
2
0 11 0 0 -1 -1 0
0<cos <1 0<cos <1-1<cos <0-1<cos <0
cos

22. Ejemplos:
1.En la C.T. ubica el ángulo de cos 220°
Desarrollo:
y
x0
220°
Cos 220°

23. 2.Señala verdadero ( V ) o falso ( F )
según corresponda.
Cos 200° > cos 260°
Desarrollo:
x
y
200°
260°
-
-
De la figura se observa
que la afirmación es falsa.
3. Ordena de menor a mayor.
cos 10°; cos 70°; cos 100°; cos 120° y
cos 300°
Desarrollo: y
x
10°
70°
100°
120°
300°
Cos 10°; cos 300°; cos 70°; cos 100°; cos 120°

24. 4.Señala la variación de L = 4 cos + 3; 60°< < 180°
Desarrollo:
x
y
60°
180°
- 1
1
2
1
1 cos
2
X 4
+ 3
4 4cos 2
1 4cos 3 5
1;5L

25. LÍNEA TRIGONOMÉTRICA TANGENTE
La tangente de un arco es la ordenada ( y ) del punto de intersección entre la recta
tangente que pasa por el origen de arcos y la prolongación del radio o diámetro
que pasa por el extremo del arco.
Ejemplos y
x
P
Tan
A
B
Tan
M
Tan
VARIACIÓN
I C II C III C IV C
+ - + -
crece crece crece crece

26. 1.Grafica la línea 2
tan
3
Desarrollo:
y
x
2
3
2
tan
3
2. será : tan300 tan340
Desarrollo:
y
x
300°
La afirmación es verdadera.

27. 3.En la C.T. encuentra el área sombreada.
Desarrollo:
En el triángulo ABC:
En el triángulo ABD:
2
2 tan
tan
2
A
1
2
2
sen
A sen
tanTA sen

28. LÍNEA TRIGONOMÉTRICA COTANGENTE
La cotangente de un arco es la abscisa ( x ) del punto de intercepción entre la
recta tangente por el origen de complementos y la prolongación del radio o
diámetro que pasa por el extremo del arco.
Ctg Ctg

29. Ejemplos:
Grafica :
2 2
cot ;cot ;cot
6 3 3
Desarrollo:
6
Cot
6
2
3
2
cot
3
2
3
2
cot
3

30. LÍNEA TRIGONOMÉTRICA SECANTE
La secante de un arco es la abscisa ( x ) del punto de intersección entre la recta
tangente que pasa por el extremo del arco y el eje x.
-Sec
Sec

31. Ejemplo:
Grafica:
2
sec ;sec
3 3
y
x
2
3
Sec
2
3
3
sec
3

32. LÍNEA TRIGONOMÉTRICA COSECANTE
La cosecante de arco es la ordenada del punto de intersección, entre la recta
tangente que pasa por el extremo de arco y el eje y
Csc Csc