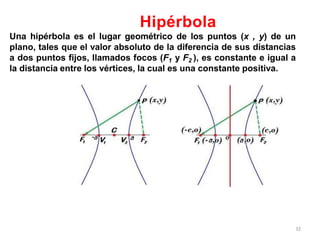
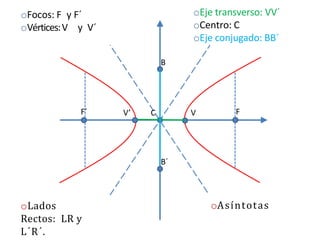
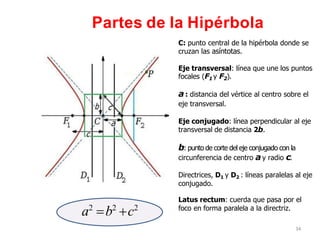
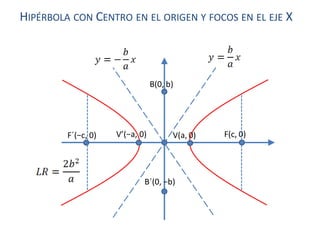
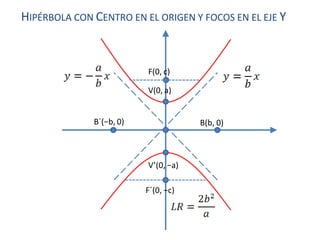
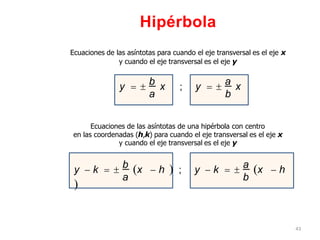
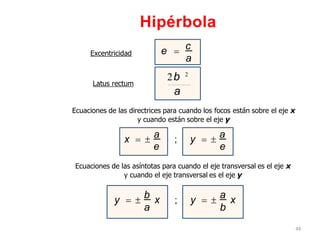
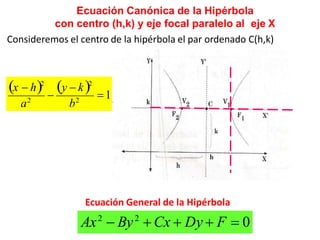
Una hipérbola es una curva plana definida como el conjunto de puntos cuyas distancias a dos puntos fijos llamados focos tienen una diferencia constante. Tiene dos vértices, un eje transversal que une los focos, y un eje conjugado perpendicular al transversal. Su ecuación canónica depende de si los focos están en el eje x o y y del centro, pudiendo ser representada como la diferencia de las distancias a los focos dividida entre una constante.

1. Hipérbola
32
Una hipérbola es el lugar geométrico de los puntos (x , y) de un
plano, tales que el valor absoluto de la diferencia de sus distancias
a dos puntos fijos, llamados focos (F1 y F2 ), es constante e igual a
la distancia entre los vértices, la cual es una constante positiva.

2. V’ V
F´ F
B´
oFocos: F y F´
oVértices:V y V´
oEje transverso: VV´
oCentro: C
oEje conjugado: BB´
B
oLados
Rectos: LR y
L´R´.
C
oAsíntotas

3. Partes de la Hipérbola
34
C: punto central de la hipérbola donde se
cruzan las asíntotas.
Eje transversal: línea que une los puntos
focales (F1 y F2).
a: distancia del vértice al centro sobre el
eje transversal.
Eje conjugado: línea perpendicular al eje
transversal de distancia 2b.
b: punto de corte del eje conjugado con la
circunferencia de centro ay radio c.
Directrices, D1 y D2 : líneas paralelas al eje
conjugado.
Latus rectum: cuerda que pasa por el
foco en forma paralela a la directriz.
a2
=b2
+c2

4. V’(−a, 0) V(a, 0)
F´(−c, 0) F(c, 0)
B(0, b)
B´(0, −b)
HIPÉRBOLA CON CENTRO EN EL ORIGEN Y FOCOS EN EL EJE X

5. Ecuación Canónica de la Hipérbola
con centro (0,0) y focos en el eje X
38
−
b2 =1
x2
y2
a2
Ax 2
− By 2
= 1
Ecuación general de una hipérbola con centro en el origen y
focos sobre los ejes de coordenadas

6. • Ecuación: ,
• Centro: C(0, 0)
• Coordenadas de sus vértices: V(a, 0) y V´(-a, 0)
• Coordenadas de los extremos del eje conjugado:
B(0, b) y B´(0, -b)
• Coordenadas de sus focos: F(c, 0) y F´(-c, 0)
• Longitud del eje transverso: VV´= 2a
• Longitud del eje conjugado: BB´=2b
• Longitud de cada lado recto:
• Excentricidad:
• Asíntotas:

7. V’(0, −a)
F´(0, −c)
F(0, c)
V(0, a)
B(b, 0)
B´(−b, 0)
HIPÉRBOLA CON CENTRO EN EL ORIGEN Y FOCOS EN EL EJE Y

8. • Ecuación: ,
• Centro: C(0, 0)
• Coordenadas de sus vértices: V(0, a) y V´(0, -a)
• Coordenadas de los extremos del eje conjugado:
B(b, 0) y B´(-b, 0)
• Coordenadas de sus focos: F(0, c) y F´(0, -c)
• Longitud del eje transverso: VV´= 2a
• Longitud del eje conjugado: BB´=2b
• Longitud de cada lado recto:
• Excentricidad:
• Asíntotas:

9. Ecuación Canónica de la
Hipérbola con centro (0,0) y
focos en el eje Y
42
1
y2
−
x2
=
a2
b2
Ax 2
− By 2
= 1
Ecuación general de una hipérbola con centro en el origen y
focos sobre los ejes de coordenadas

10. Hipérbola
43
a b
y − k = 
b (x − h ) ; y − k = 
a (x − h
)
Ecuaciones de las asíntotas de una hipérbola con centro
en las coordenadas (h,k) para cuando el eje transversal es el eje x
y cuando el eje transversal es el eje y
Ecuaciones de las asíntotas para cuando el eje transversal es el eje x
y cuando el eje transversal es el eje y
a b
y = 
b x ; y = 
a x

11. Hipérbola
44
a b
y = 
b x ; y = 
a x
Excentricidad
Ecuaciones de las directrices para cuando los focos están sobre el eje x
y cuando están sobre el eje y
Latus rectum
Ecuaciones de las asíntotas para cuando el eje transversal es el eje x
y cuando el eje transversal es el eje y
a
e =
c
2b 2
a
e e
x =  a ; y =  a

12. Ecuación Canónica de la Hipérbola
con centro (h,k) y eje focal paralelo al eje X
Consideremos el centro de la hipérbola el par ordenado C(h,k)
=1
−
b2
(y − k)2
a2
(x − h)2
Ecuación General de la Hipérbola
Ax2
− By2
+ Cx + Dy + F = 0

13. =1
−
b2
(x − h)2
a2
(y − k
)2
Ecuación General de la Hipérbola
Ay2
− Bx2
+ Cx + Dy + F = 0
Ecuación Canónica de la Hipérbola
con centro (h,k) y eje focal paralelo al eje Y

14. Ecuación Canónica de la Hipérbola
con centro (h,k)
47
Si el centro de la hipérbola tiene coordenadas (h,k) y eje transversal
paralelo al eje x
=1
(x−h)2
−
(y−k)2
a2
b2
=1
(y −k)2
−
(x −h)2
a2
b2
Si el centro de la hipérbola tiene coordenadas (h,k) y eje transversal
paralelo al eje y
Ecuación general de una hipérbola con centro en las coordenadas (h,k) y
ejes paralelos a los de las coordenadas x y y, siendo A y B del mismo signo
Ax 2
− By 2
+ Dx + Ey + F = 0