Descargado 62 veces
Subido pormaria angela muñoz
matematicas modulo 2
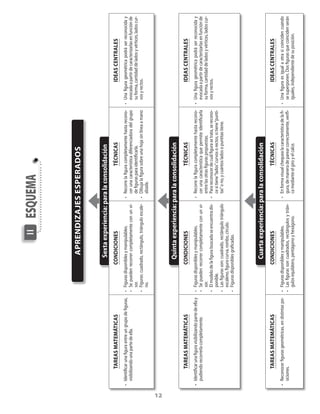
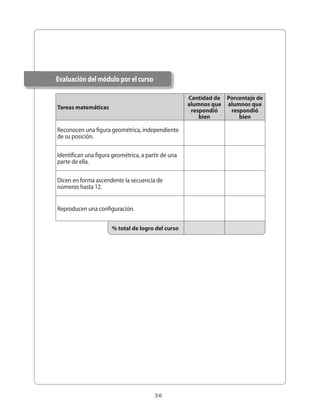
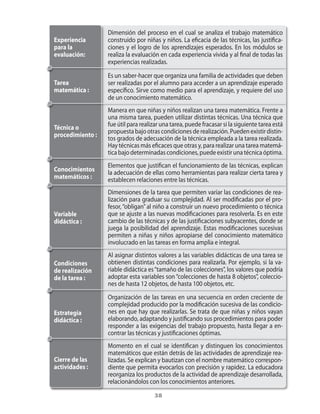
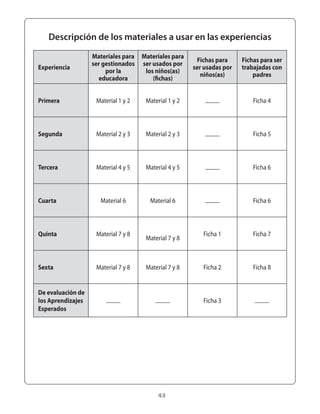
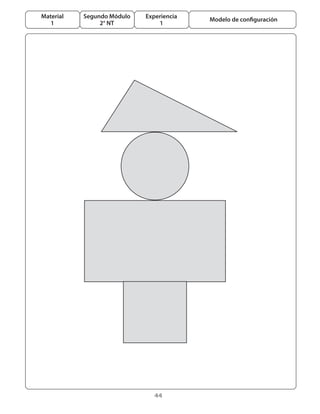
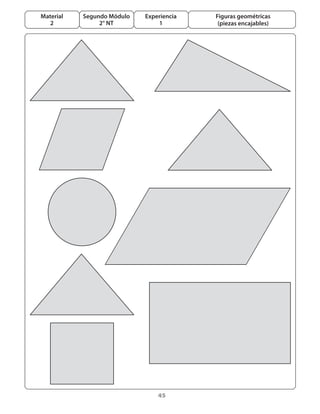
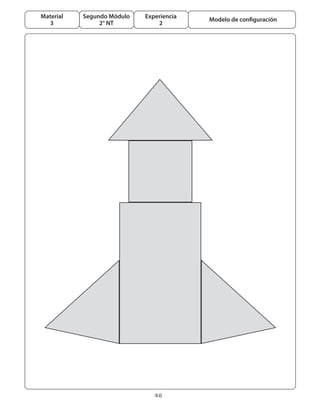
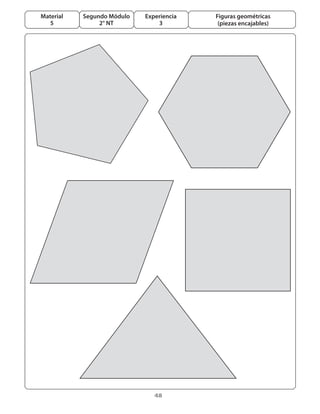
Este documento presenta un módulo educativo sobre formas y figuras geométricas para estudiantes de segundo nivel de transición. 1) Introduce las tareas, variables didácticas, procedimientos y ideas centrales del módulo. 2) Describe el proceso de enseñanza y aprendizaje que incluye seis experiencias graduadas, con actividades exploratorias, de consolidación y evaluación. 3) El objetivo es que los estudiantes reconozcan atributos de figuras geométricas y puedan reproducir y completar configuraciones.
matematicas modulo 2
- 1. 2° NivelTransición Educación Parvularia Módulo2 Formas y figuras geométricas GuíaDidáctica EDUCACIÓN MATEMÁTICA
- 2. Formas y figuras geométricas •• Autores • • Matemática Segundo Módulo Educación Parvularia segundo nivel de transición primer semestre Lorena Espinoza • Enrique González • María Paz Silva • Patricio Stuardo • Dinko Mitrovich G.
- 4. Índice I Presentación 6 II Esquema 12 III Estrategia didáctica 14 IV Planes de clases 28 V Sugerencia de Actividades para trabajar con la familia 34 Evaluación del módulo por el curso 36 VI Glosario 37 Bibliografía 39 VII Materiales y Fichas para alumnas y alumnos 41
- 6. SEGUNDO módulo segundONIVELdeTRAnsición educaciónparvularia Formas yfiguras geométricas Matemática • Reconocer figuras en objetos del entorno. • Construir configuraciones con figuras geométricas, en forma libre. • Reproducir una configuración en la que se dispone de las figuras y el modelo de la configuración, simultáneamente y en el mismo plano. • Enumerar y contar colecciones hasta 12 objetos. Aprendizajes previos • Reconocen figuras geométricas a partir de sus características, tales como su forma, si tiene los lados rectos o curvos, y por la cantidad de vértices y lados que tiene. • Reproducen y completan configuraciones formadas con figuras geométricas. Aprendizajes esperados para el Módulo • Reconocer algunos atributos, propiedades y nociones de algunos cuerpos y figuras geométricas en dos dimensiones, en objetos, dibujos y construcciones (Aprendizaje esperado 3). • Describir la posición de diferentes objetos en el espacio y las variaciones en cuanto a forma y tamaño que se pueden percibir como resultado de las diferentes ubicaciones de los observadores (Aprendizaje esperado 7). Aprendizajes esperados de las bases curriculares Aprendizajes esperados de Primer Año Básico que se articulan con el Módulo • Asocian formas geométricas de una, dos y tres dimensiones con objetos presen- tes en el entorno, las nombran y reconocen en ellas elementos curvos, rectos o planos que las conforman (Aprendizaje esperado 7, primer semestre)
- 7. 1. presentaciónI E 2. n este móduloniños y niñas se enfrentarán a problemas relativos a reproducir o completar una configuración. Para resolverlos deberán elegir entre varias figuras aquellas que les sirven. La elección les significará poner a prueba sus conocimientos, avanzando desde la percepción global de la figuras, hasta comenzar a distinguir algunos de los elementos y sus características. A continuación se detallan los aspectos didácticos matemáticos que estructuran este módulo. Tareas matemáticas Las tareas matemáticas que niñas y niños realizan para lograr los aprendizajes es- perados de este módulo son: Reproducen una configuración formada por figuras geométricas. Reconocen en una configuración, la figura que la completa. Reconocen figuras geométricas, en distintas posiciones. Identifican una figura visibilizando parte de ella y pudiendo recorrerla comple- tamente. Variables didácticas Las variables didácticas que se consideran para graduar la complejidad de las ta- reas matemáticas que niñas y niños realizan son: Características de las figuras: cantidad de lados y vértices; con lados curvos o rectos y tipo de figuras: cuadrado, rectángulo, pentágono, hexágono, trián- gulo. Disponibilidad de las figuras y de las configuraciones para su reproducción: visible permanente o momentáneamente. Las figuras pueden o no estar disponibles simultáneamente con la configuración.
- 8. Presentación Características dela configuración: se asemeja o no a objetos reales, encajable (rompecabezas), cantidad y variedad de las figuras que la componen, posición de la figura. Posición de la configuración: se puede encontrar en un plano vertical u hori- zontal. Procedimientos Los procedimientos que los niños y niñas construyen y se apropian para realizar las tareas matemáticas son: Para reproducir o completar una configuración, reconocen las figuras: Porque tienen lados rectos o curvos. Asociándola a la forma de la configuración, según la parte que parece del objeto real al que se asemeja la configuración. Por la cantidad de lados o vértices que tiene. Para reconocer que dos figuras son iguales: En forma visual chequean las características de la figura. Las giran para comprobar que coincide. Para identificar una figura que la pueden ver parcialmente: La recorren completamente hasta reconocer una característica que la distinga de la figuras que tienen para seleccionar. Ideas centrales del módulo Una figura geométrica podrá ser reconocida y evocada a partir de caracterizar- las en función de su forma, cantidad de lados o vértices, lados curvos o rectos. Asimismo, en una instancia preliminar una figura podrá ser reconocida dentro de una configuración por asociación con el objeto real al que se asemeja la con- figuración. 3. 4.
- 9. Presentación Una figuraes igual a otra si coinciden cuando se superponen. Dos figuras que coinciden serán iguales, independiente de su posición. Un grupo de figuras que se encuentran yuxtapuestas por sus lados o vértices constituyen una configuración, independiente de si se asemejan a un objeto real. Una figura no cambia sus características de forma, cantidad de lados y vértices, si se la gira o traslada. Descripción global del proceso En el presente módulo se propone un proceso organizado sobre la base de 6 expe- riencias de aprendizaje, las que forman parte de una secuencia organizada, con criterios didácticos, para ser desarrolladas en los períodos variables; conjuntamente, se propo- nen actividades complementarias para los períodos permanentes. Las seis experiencias de aprendizaje, componen un proceso de enseñanza-apren- dizaje, contribuyendo para que los niños y niñas avancen desde sus conocimientos previos hasta alcanzar los aprendizajes esperados. Las experiencias de aprendizaje han sido secuenciadas con la intención de hacer vivir a los niños un proceso que, gradualmente, les permita ir encontrándose con las nociones matemáticas que se estudian y, de esta forma, construyendo su significado. La gradualidad de este proceso se consigue planteando diferentes tareas matemá- ticas para las experiencias de aprendizaje y modificando las variables didácticas que se han seleccionado. Cada experiencia de aprendizaje corresponde a un momento del proceso con carac- terísticas específicas. Por este motivo, y para hacerlas evidentes, se les ha denominado de forma diferente: Experiencias para la exploración, experiencias para la consolidación y experiencias para la evaluación. A continuación se caracterizan los tres tipos de experiencias de aprendizaje: Experiencias para la exploración: Son experiencias en las que se proponen activida- des donde niños y niñas se verán enfrentados a resolver problemas nuevos para ellos, vale decir, que los conocimientos disponibles hasta el momento no les serán suficientes para resolverlos. 5.
- 10. Presentación En este tipode experiencias es fundamental que se cuiden las condiciones propuestas, de manera que los niños tengan realmente la posibilidad de indagar, probar procedimientos e intercambiar ideas para intentar resolver la situación que se les propone. Experiencias para la consolidación: Las actividades propuestas para este tipo de experiencias buscan que niños y niñas afiancen los procedimientos que les han fun- cionado en las experiencias de exploración. Se proponen problemas en que, para que puedan resolverlos, tendrán que poner en juego los conocimientos matemáticos que están en proceso de construcción. De ahí la importancia de que en este tipo de activi- dad, la educadora gestione que los niños intercambien sus procedimientos, y genere las condiciones para que expliquen lo que hicieron para resolver el problema, relevando los procedimientos más eficaces. En este tipo de experiencias la educadora debe ayudar a los niños y niñas a ponerle nombre a las nociones con las que se está trabajando, en la medida que sea necesario. Experiencias para la evaluación: la dimensión evaluativa es considerada en todas las experiencias de aprendizajes, ya que es parte inseparable del aprender y enseñar matemática. Esto último se expresa en los planes de las experiencias, donde los indi- cadores propuestos permiten develar como participa esta dimensión en el proceso de enseñanza y aprendizaje. No obstante, las experiencias para la evaluación se proponen al finalizar el proceso, con la intención de evidenciar el progreso logrado por los niños y niñas en relación al logro de los aprendizajes esperados. El proceso parte con la primera y segunda experiencia: para exploración. Los niños y niñas deberán abordar una misma problemática, que consiste en reproducir una configuración que tiene una forma semejante a un objeto real. Se diferencian en que en la primera experiencia, el modelo de la configuración se encuentra disponible, mientras que en la segunda experiencia verán la configuración solo por un momento, debiendo recordar las figuras para formar la configuración. Enlaterceraexperiencia:paralaexploración,seintenta“forzar” alosniñosyniñas a buscar estrategias para reconocer la figura, basados en las características geométricas de ella. Se espera que aquellos niños y niñas que aún seleccionan las figuras basados en atributos no geométricos, se vean enfrentados a la necesidad de avanzar en sus conoci- mientos. Para ello, deberán enfrentarse al problema de completar una configuración en la que falta una figura de varios lados. En la cuarta experiencia: para la consolidación, niños y niñas realizarán una ac- tividad que les pondrá ante la situación de identificar una figura que se encuentre en
- 11. 10 Presentación distintas posiciones. Seexplicita que una figura no cambia sus características de forma, tamaño, cantidad de lados y vértices, si se la gira o traslada. En la Quinta experiencia: para la consolidación, niños y niñas se enfrentan a un problema que consiste en identificar una figura al verla parcialmente mediante un dispositivo. A través de este problema, tendrán una nueva oportunidad de encontrarse con las figuras geométricas y distinguirlas a partir de caracterizarlas por sus elementos: lados y vértices. Cualquier otro atributo no podrá ser usado aquí, ya que la figura no es parte de una configuración y no es posible ver completamente la forma que tiene; la identificación se hará recorriendo parcialmente la figura. En la Sexta experiencia: para la consolidación, se propone una actividad similar, donde deben reconocer una figura que está bajo el visor, identificándola por sus carac- terísticas y dibujarla en una hoja en blanco. Sugerencias para verificar los Aprendizajes Previos Antes de dar inicio al estudio del módulo, es necesario realizar un trabajo sobre los aprendizajes previos. Interesa que niñas y niños activen los conocimientos necesarios para que puedan enfrentar adecuadamente el módulo y lograr los aprendizajes espera- dos en este. La educadora debe asegurarse de que todos los niños y niñas: Reconozcan figuras en objetos del entorno. Presente objetos, que sus caras tengan formas de cuadrado, triángulo y círculo. Después, mostrando una figura, por ejemplo, un triángulo, pregunte: ¿En cuál de estos objetos hay una forma parecida a esta? Construir configuraciones con figuras geométricas, en forma libre. Ponga a disposición diferentes figuras geométricas y pida que armen una nueva figura con ellas, que se parezca a un objeto, animal o cosa conocida por ellos. Una vez realizada la construcción, pida que cuenten a qué se parece. Reproducir una configuración en la que se dispone de las figuras y el modelo de la configuración, simultáneamente y en el mismo plano. Entregue figuras geométricas y una configuración en las que se utilicen las mismas figuras, y pida que armen una igual. 6.
- 12. 11 Presentación Contar colecciones hasta12 objetos. Para el logro de estos aprendizajes se propone la realización de las actividades del Primer Módulo de Segundo Nivel de Transición:“Enumerar y contar con números hasta 12”.
- 13.
- 14.
- 15. 14 estrategiadidácticaIII Como se describióanteriormente, las actividades propuestas en este módulo per- miten a niños y niñas del segundo nivel de transición, el reconocimiento de algunas figuras geométricas. El proceso abordado para este módulo se desarrolla presentando diferentes activi- dades, tanto para los períodos permanentes como para los períodos variables; a través de este proceso se espera que niños y niñas construyan gradualmente las nociones para caracterizar figuras geométricas. La gradualidad de este proceso se consigue modifican- do las variables didácticas señaladas. No obstante, una característica geométrica como el tamaño no varía, de manera que en cada experiencia no aparecen dos figuras iguales de distinto tamaño. Se ha cuidado que otras características de las figuras, como el color o textura, sean de un mismo tipo, para evitar que los niños vayan a identificar la figura por estas características. En el desarrollo de las actividades de este módulo se recomienda que la educa- dora: Rescate los saberes previos de niñas y niños. Desafíe a niños y niñas frente a un problema y los haga sentir capaces de resol- verlo. Procure que comprendan las consignas. La consigna debe ser clara y no aportar información que les diga cómo resolver el problema. Permita que niños y niñas utilicen los términos que para ellos resultan con más sentido para nombrar elementos de las figuras; no fuerce la utilización de térmi- nos formales. Promueva que expliciten sus ideas y procedimientos para resolver un problema, aun cuando se trate de una idea errada, pues la justificación de que existe un error es una instancia de aprendizaje. Sistematice los conocimientos surgidos durante la realización de la actividad; para ello, promueva a través de preguntas que los niños expliquen qué hicieron para solucionar el problema y releve aquellos conocimientos según lo señalado en las ideas centrales de cada experiencia.
- 16. 15 Orientaciones A continuación aparecendescritas las actividades propuestas en las experiencias del módulo que corresponden a los períodos variables, señalando las ideas didácticas que dan fundamento a las acciones que realiza la educadora en cada experiencia. En esta primera experiencia se pretende que niñas y niños tengan un primer en- cuentro con las figuras geométricas desde un punto de vista matemático. Para ello, se propone una actividad llamada Copiando la figura, que plantea la tarea matemática de reproducir una configuración formada por figuras geométricas que se encuentran disponi- bles en la pizarra. La condición prevista en esta experiencia, es restringir la posibilidad de copiar la configuración mediante la superposición, por esto, se propone que se encuentre pega- da en la pizarra para que los niños la tengan visible. Se propone comenzar por mostrarles a niños y niñas una configuración Material 1 con las figuras encajadas y preguntarles ¿a qué se parece? Esto con la intención de que asocien la configuración con algún objeto del entorno que conozcan. No se debe esperar ni intencionar que todos “vean” lo mismo, algunos podrán percibir a una persona sentada, mientras que otros podrán imaginar un sillón con una lámpara; lo que importa es que lo percibido les pueda ayudar a reconocer las figuras que forman la configuración como partes de un objeto. Con esta primera acti- vidad se pretende relacionar los conocimientos previos que tengan niñas y niños para reconocer figuras geométricas, que en esta ocasión, probablemente, se centren en atri- butos no matemáticos; por ejemplo, esta figura es el sombrero (señalando un triángulo) de la persona o que seleccionen un triángulo, porque imaginaron que era la pantalla de una lámpara. PRIMERA EXPERIENCIA: para la exploración
- 17. 16 Orientaciones Una vez vistala configuración y comentado a qué se parece, explique que cada uno tendrá que formar una figura exactamente igual. Para ello entregue el Material 2 y señale que: cada uno deberá ver bien qué figuras necesita e ir a buscar las figuras para armar la configuración. Tienen sólo una oportunidad para ir a buscar las figuras necesarias, no pueden faltar o sobrar figuras. Para el logro del propósito de esta actividad, que consiste en que los niños y ni- ñas empiecen a reconocer figuras geométricas a partir de algunas de sus características geométricas, se proponen configuraciones con figuras que los niños ya conocen: cua- drado, triángulo, rectángulo y círculo. El desafío para niños y niñas, será identificar estas figuras entre otras que tienen características similares. Por este motivo, en la colección se ha introducido un paralelogramo y un rombo que tiene“puntas”similares al triángulo y tienen 4 lados como el cuadrado. En la gestión de la actividad se deberá buscar que los niños agudicen su mirada, dis- tinguiendo algunas características de los elementos que constituyen las figuras, como son la cantidad de “puntas” o “puntitas” (vértices), si entre los lados algunos son más largos o si algunas son“más puntudas que otras”(ángulos). Organice dos o más lugares de la sala donde poner las figuras, para que los niños vayan a buscarlas ordenadamente, evitando que se aglomeren, cuestión que puede perjudicar su concentración en la elección. Una vez que seleccionen las figuras, observe si han elegido las figuras que corres- ponden. En caso contrario, detecte qué les puede haber llevado a equivocarse. Puede que algunos niños o niñas hayan sacado más o menos figuras; si esto ocurre, se reco- mienda proponerles que las devuelvan todas y lo intenten nuevamente mirando bien la configuración.
- 18. 17 Orientaciones Evite decir sila selección hecha por los niños está bien o mal. Tenga en cuenta que el diseño de la actividad considera que una vez que hayan seleccionado las figuras, de- berán encajarlas; de esta forma podrán darse cuenta si las figuras elegidas fueron las correctas. Cuando todos los niños hayan ido a buscar las figuras e intentado armar la confi- guración, promueva que compartan si lograron armar la configuración. Para ello platee preguntas como: ¿Quiénes no lograron completar la figura? ¿Cuál figura les faltó? ¿Por qué creyeron que les serviría una y no la otra? ¿Quiénes lograron completar la figura? ¿En qué se fijaron para seleccionar las figuras? Se trata de no personalizar los comentarios ni las preguntas, ni promover respuesta a“coro”. Se debe plantear de manera que todos se sientan involucrados y propiciando una gestión en que respondan algunos niños y niñas. Se busca que los argumentos para identificar las figuras que forman la configuración, surjan de los propios niños, por lo que es importante considerar los errores y utilizarlos como instancia de aprendi- zaje. Al cierre de la experiencia sistematice los argumentos propuestos por niñas y niños para identificar las figuras, por ejemplo: ¿En qué se fijan para elegir esta figura (mostran- do el triángulo)? Se espera que respondan con expresiones del tipo: tiene“3 puntas”, o es la figura que es más“puntuda”, o es la figura que tiene 3“lados”. De la misma forma, muestre un rectángulo o un cuadrado para que expliquen en qué habría que fijarse para seleccionarlo. Una vez que ha mostrado la figura y la ha caracterizado conforme al lenguaje empleado por los niños, pregunte si alguien conoce el nombre de ella; en el caso de que nadie lo mencione, solo dé el nombre de aquellas figuras que forman la configuración: cuadrado, triángulo, rectángulo y círculo. Una buena forma para que los niños avancen en las características de las figuras es mostrarles dos figuras, una que esté en la configuración y otra que esté en la colección de figuras para seleccionar y preguntarles: ¿Cuál de estas seleccionarían para poner aquí? (Señalando una parte de la configuración). En esta experiencia, la tarea matemática propuesta consiste en reproducir una con- figuración formada por figuras geométricas, algunas de ellas repetidas, dispuestas de tal forma que el niño o niña lo reconozca semejante a un objeto real. Para esto, se propone una actividad similar a la primera experiencia exploratoria, llamada Construyendo figuras, en que se propone mostrar la configuración del Ma- terial 3 y preguntar a qué se parece, de manera que lo asocien con algún objeto del SEGUNDA EXPERIENCIA: para la exploración
- 19. 18 Orientaciones mundo real. Conla intención de producir un progreso en el proceso de reconocer ca- racterísticas de figuras, se propone que la configuración ya no esté disponible siempre, sino solo por un momento. Para tal efecto, se propone que la consigna contemple dos momentos. Cuando la educadora muestre el modelo de la configuración, señale: “observen bien el modelo, porque tendrán que venir a buscar las figuras necesarias para completar la plantilla”. Una vez que se ha retirado el modelo de la pizarra, se pide:“cada uno vendrá en un solo viaje a buscar las figuras necesarias para completar la plantilla. Las condiciones descritas posibilitan que el niño necesite centrar su reconocimiento en las características de la figura. La restricción de ir a buscar las figuras en un solo viaje pretende evitar la elección de la figura por ensayo y error. Sin esta restricción, se da la posibilidad al niño de tomar cualquier figura, probar si calza en la plantilla e ir a buscar otra. Los materiales que se utilizarán en esta actividad son la configuración, una plantilla y un set de figuras. Para reproducir la configuración se utilizará la plantilla en la que calzan por encaje las figuras que la conforman. La característica de encajar tiene como propósito que niñas y niños reconozcan en forma inmediata que las figuras que selec- cionaron son las que permiten reconstruir la configuración.
- 20. 19 Orientaciones En cuanto altipo de figuras, se mantienen las mismas de la primera experiencia, Material 2; sin embargo, se ha incorporado en la configuración más de una figura del mismo tipo, porque se pretende poner en juego el reconocimiento de que dos figuras son iguales, independiente de su posición. Al cierre de la actividad se dispondrá de la configuración en la pizarra; pida que nombren las figuras que componen cada configuración, de manera que vinculen la for- ma de la figura con el nombre correspondiente y que reconozcan que, aunque cambie de posición, es la misma figura. Realice preguntas del tipo: ¿Qué fue necesario hacer? ¿Se puede saber si dos figuras en distinta posición son la misma? En esta experiencia la tarea matemática propuesta consiste en reconocer la figura que completa una configuración; para ello deberán seleccionarla de entre otras figuras la que calza. La actividad propuesta se denomina Completando la estrella y con ella se desafía a niñas y niños a identificar una figura de 5 lados, seleccionándola entre otras figuras. De esta forma se intenta “forzar” a que quienes aún seleccionan las figuras basados en atributos no geométricos, a buscar nuevas estrategias para reconocerlas. La configuración por completar corresponde a una estrella Material 4, que el niño debe ser capaz de percibir como incompleta; para que esto se haga evidente, la educa- dora presenta la configuración completa, inmediatamente después saca el centro de ella, dejando el sacado. TERCERA EXPERIENCIA: para la exploración
- 21. 20 Orientaciones Para el desarrollode la experiencia, existe una restricción importante, el niño debe elegir de una colección de figuras aquella que calza Material 5. Esto lo debe hacer en un sólo viaje, evitando así el ensayo y error para seleccionar la figura que calce y completar la estrella. Es importante resaltar que quienes no logren reconocer y completar la configura- ción, pueden verificar de forma inmediata que no es la figura, pues no lograran calzarla. La educadora debe posibilitar que niñas y niños manifiesten que algo ha ocurrido, que indica con sus palabras “que no se puede calzar”. Esto da la oportunidad, una vez que todos han terminado, para realizar las preguntas indagatorias que permitan a los niños contrastar su forma de seleccionar la figura. Preguntar, por ejemplo: ¿Qué tiene esta figura que no calza en la estrella? ¿En qué te fijaste para seleccionarla? ¿En qué te fijarías si te diera una nueva oportunidad para ir a buscarla? De la misma forma, promueva que quienes identificaron la figura, expliquen en qué se fijaron para seleccionarla. Posibilite que manifiesten diversas explicaciones, centran- do la atención de los niños en aquellas que se refieran a la cuantificación de lados y vértices, refiriéndose a estos dos últimos términos como mejor les acomode a los niños. En experiencias anteriores se ha detectado que a los lados le llaman “guatitas” y a los vértices“puntas”.
- 22. 21 Orientaciones Una vez finalizadoel momento en que los niños compartieron y compararon sus procedimientos, releve y enfatice aquellos que funcionan, es decir, aquellos basados en contar los lados y/o los vértices. En esta experiencia, se propone una actividad en que la tarea matemática consiste en reconocer figuras geométricas iguales presentadas en diferentes posiciones. En experiencias anteriores, cuando han reconocido figuras para completar una con- figuración, se ha encontrado implícito identificar que una figura es igual a otra, aunque se encuentren en distinta posición. En esta experiencia con la actividad propuesta Ar- mando la cadena, se busca explicitar la propiedad de que una figura no cambia sus características de forma, cantidad de lados y vértices, si se la gira o traslada. Por esto, esta experiencia es considerada de consolidación. Para la realización de la actividad, se utiliza un material compuesto por 15 piezas Material 6; los extremos son dos figuras como se muestra a continuación. Las figuras geométricas de los extremos son cinco: triángulo equilátero, cuadrado, rectángulo, pentágono, hexágono. Antes de iniciar la actividad, la educadora debe mostrar el gesto de unir dos piezas por uno de sus lados, señalando que se pueden unir por más de un lado. CUARTA EXPERIENCIA: para la consolidación
- 23. 22 Orientaciones Se disponen laspiezas sobre la mesa dentro de una caja o bandeja, de manera que permita que todos los niños puedan ver las figuras. Quien saca la primera pieza, inicia la construcción y, a partir de esta pieza, se irán encadenando las figuras, uniendo figuras iguales, por uno de sus lados (yuxtaposición). Es importante destacar que cada figura puede ser yuxtapuesta por más de un lado, quedando una cadena lineal o una a partir de un nodo. La actividad requiere que los niños y niñas respeten el turno. Para lograr que niñas y niños comprendan lo que tienen que hacer, es importante cuidar la consigna que se les proponga. Un ejemplo de consigna puede ser“van a for- mar una cadena, colocando juntas figuras que sean iguales, respetando el turno y colocando una a la vez”. Una vez que se retira una pieza, los niños y niñas mirarán las figuras que tiene su pieza y buscarán dónde ubicarla; una vez puesta, el grupo revisará el trabajo de su compañero(a) por superposición de las figuras; si verifican que la ubicación de la figura es incorrecta, se devolverá la pieza a la caja y le corresponderá al siguiente continuar la actividad. La yuxtaposición correcta no sólo estará controlada por la técnica de verificación mediante la superposición, sino también por los niños que ya han reconocido la igual- dad de la figura. Para abordar la problemática de armar la cadena, se espera que niñas y niños ela- boren una técnica que pasa por el reconocimiento de la figura geométrica mediante la superposición y el giro apropiado. El material empleado posibilita que el niño lo manipu- le, realice las comparaciones y verifique que dos figuras son iguales, porque es posible hacerlas coincidir. Terminada la construcción en cada grupo, la educadora preguntará: ¿A algún gru- po le ha quedado alguna pieza que no ha logrado parear? Los grupos que señalen esta situación, conversarán con todo el curso para ver qué pasó.
- 24. 23 Orientaciones En el cierre,se propone simular la presentación de dos piezas, en que los extremos pareables difieren en la posición de las figuras. Por ejemplo, se espera que algunos ni- ños señalen que son pareables, porque son iguales, y otros que no. Es importante que la educadora identifique a quienes, durante el juego, no logran reconocer dos piezas pareables en figuras con distinta posición, para que puedan participar en esta discusión y realizar la superposición de las figuras, de manera que verifique personalmente que sí son iguales.
- 25. 24 Orientaciones El problema alque se enfrentarán niñas y niños en esta experiencia, consiste en identificar una figura visibilizando parte de ella. A través de la actividad denominada ¿qué figura es?, los niños tendrán una nueva oportunidad de encontrarse con las figuras geométricas y distinguirlas a partir de ca- racterísticas de dos de sus elementos: lados y vértices. Cualquier otro atributo aquí no podrá ser usado ya que la figura no es parte de una configuración y no es posible ver completamente la forma que tiene. Para plasmar en una actividad lo anteriormente dicho, en la experiencia se utiliza un recurso que se ha denominado “visor”1 Material 7, confeccionado en un material rígido y no traslúcido, del tamaño de una hoja carta con una perforación circular al centro; el diámetro de esta perforación permite visualizar solo parte de las figuras del Material 8. La actividad se realiza en pareja, recibiendo cada pareja un sobre con las figuras del Material 8 y el visor. Un niño o niña de la pareja, selecciona una figura del sobre y la co- loca bajo el visor, cautelando que el otro niño no pueda ver la figura que se coloca bajo el visor. Luego, este recorrerá la figura moviendo el visor, pero sin levantarlo. El tamaño del orificio del visor y el de la figura, cautela que el niño no pueda ver más de la mitad de la figura. QUINTA EXPERIENCIA: para la consolidación 1 El uso del visor se propone en Gálvez, Grecia (1985). El aprendizaje en la orientación en el espacio urbano.
- 26. 25 Orientaciones El procedimiento queel niño o niña puede emplear para identificar la figura, consis- te en chequear si la parte que visualiza de la figura, es una característica que le permita identificarla y marcar su respuesta en la Ficha1, que tiene las figuras empleadas para ser recorridas por el visor entre otras figuras. El recorrido con el visor variará según la figura que esté debajo. En experiencias an- teriores se ha observado que, guiándose por la ficha de respuesta, el niño o niña realiza un recorrido chequeando si lo que visualiza es similar a la figura de la ficha. Para identificar, se espera que el procedimiento más eficaz sea que el niño o niña cuente el número de lados o vértices mediante el recorrido con el visor. En el cierre, las preguntas planteadas esperan que la justificación haga mención de la característica distintiva, utilizando las palabras que niñas y niños han empleado para el reconocimiento de la figura bajo el visor. Se discutirá si alguno se centró primero en el vértice, para luego verificar el largo del lado, o lo hizo en otro orden; toda esta información posibilitará que la educadora señale que hay figuras que comparten algunas características comunes que no permiten di- ferenciarlas. Sea el caso del cuadrado y el rectángulo que tienen“la misma puntita”y la misma cantidad de ellas, y que la forma de diferenciarlas es verificar cuál de ellas tiene un lado más largo, mediante el movimiento del visor. El propósito de esta experiencia es reforzar y profundizar la tarea matemática de identificar una figura entre un grupo de figuras, visibilizando una parte de ella. Para propiciar que los procedimientos evolucionen, la actividad propuesta ¿Quién soy, dibújame? dispone el trabajo en pareja y la utilización del visor Material 7, pero a diferencia de la experiencia anterior, se utilizan solo ciertas figuras del Material 8: trián- gulo, cuadrado y rectángulo. SEXTA EXPERIENCIA: para la consolidación
- 27. 26 Orientaciones Esta restricción dela cantidad de figuras es necesaria, ya que se pedirá al niño o niña que identifique una figura sin tener un posible modelo a la vista y que luego la dibuje en la Ficha 2. Con estas condiciones, niñas y niños deberán evocar la figura oculta bajo el visor y dibujarla completa, a partir de ir visibilizándola parcialmente. Todo esto significará que consideren todas aquellas características de la figura que permita su trazado: cantidad de lados y la abertura entre los lados. Respecto al reconocimiento en el dibujo de algunas características de la figura, es- peramos que sea factible reconocer en él la cantidad de lados, y que el trazado de los lados permita diferenciar que son líneas rectas. Quizás, el cuadrado no tendrá todos sus lados iguales, pero se distinguirá claramente del rectángulo. La presentación de algunos dibujos al cierre de la experiencia, posibilitará que los niños nombren las figuras y señalen algunas de sus características. Sugerencias para trabajar estos temas en períodos permanentes Consideramos como períodos permanentes a aquellos momentos que son parte de la rutina de los niños y de la educadora en este nivel: saludo, desayuno, aseo, colación, recreación, entre otros. En estos momentos, sugerimos que la educadora aproveche las situaciones que naturalmente den la oportunidad para utilizar, profundizar o reforzar las nociones que se están estudiando en los períodos variables. Pensando en ello, se realizan sugerencias específicas para este módulo, referidas a los aspectos que la educadora puede potenciar en estas interacciones.
- 28. 27 Orientaciones Actividades sugeridas: Identificarla forma de algunos objetos, por ejemplo: en la colación, por la forma del plato, la galleta. Buscar en su entorno objetos que tengan una determinada forma, ejemplo: rectángulo. Formar figuras grupalmente o con su cuerpo, por ejemplo: hagan una ronda, siéntense en el suelo en forma de rectángulo. Las actividades propuestas en los aprendizajes previos que tienen que ver con el contar son pertinentes para ser realizadas en períodos permanentes.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35. 34 Se presenta unconjunto de actividades separadas por experiencias, con el fin de que se trabajen en el hogar para apoyar el trabajo que los niños realizan en la escuela. Esto facilitará a futuro una mejor y mayor comprensión de los aprendizajes que se estu- dian en la escuela. La familia cumple el rol de facilitar la realización de las actividades, buscando el momento y el lugar más adecuado, pero son los propios niños y niñas quie- nes tienen que realizarlas. Actividades para la primera experiencia de aprendizaje: Se propone realizar la actividad de“Mi cuaderno de matemáticas”referida a:“cons- truye una figura”. Para esto, madres y padres contarán con la Ficha 4 de figuras geomé- tricas, las que deberán recortar para que el niño o niña construya una figura en forma libre. Una vez terminada, pregúntele ¿qué hizo?, ¿cómo son estas figuras? Actividades para la segunda experiencia de aprendizaje: Se propone realizar la actividad de “Mi cuaderno de matemáticas” referida a: “pin- tando el borde de las figuras”. Para esto, madres y padres contarán con la Ficha 5 en que aparecen figuras geométricas, donde el niño o niña, deberá pintar solo el contorno de las figuras. Actividades para la tercera experiencia de aprendizaje: Para este día se propone realizar la actividad de “Mi cuaderno de matemáticas” re- ferida a:“recortar un cuadrado o rectángulo de revista o diarios”pegando la figura en la Ficha 6. Actividades para la cuarta experiencia de aprendizaje: Se propone realizar la actividad de“Mi cuaderno de matemáticas”referida a:“com- pletando la figura”, donde tendrán la Ficha 7 en que aparecen unas figuras incompletas, las que deberán completar uniendo sus extremos. Actividades para la sexta experiencia de aprendizaje: Para este experiencia se propone realizar la actividad de“Mi cuaderno de matemáti- cas”referida a:“marca la figura que se ha tapado con el visor”, donde deberán marcar la figura que está oculta, Ficha 8. sugerenciasdeactividadesparatrabajar conlafamilia V
- 36. 35 Sugerencias de actividades Sugerencias de actividades para la experiencia de evaluación de los aprendizajes esperados de este módulo Reproducir una configuración que contiene figuras geométricas. Puede formar otras configuraciones a partir de las figuras disponibles de los Mate- riales 2 y 5, marcando el contorno de esta nueva configuración y variando las condicio- nes de realización, según la primera y segunda experiencia de exploración. Reconocer una figura que completa una configuración Identificar una figura visibilizando parte de ella
- 37. 36 % total delogro del curso Evaluación del módulo por el curso Tareas matemáticas Cantidad de alumnos que respondió bien Porcentaje de alumnos que respondió bien Reconocen una figura geométrica, independiente de su posición. Identifican una figura geométrica, a partir de una parte de ella. Dicen en forma ascendente la secuencia de números hasta 12. Reproducen una configuración.
- 38. 37 GlosarioVI Unir una figuracon otra, haciendo coincidir dos lados de ambas figu- ras. Yuxtaponer : Superponer : Unir una figura con otra, haciendo coincidir las dos caras de las figu- ras. Configuración : Figura : Objeto geométrico delimitado por líneas curvas o rectas. Matemático Didáctico Instancia en la cual la educadora presenta una o más actividades que permiten a niñas y niños trabajar sobre actividades que involucran conocimientos matemáticos. Experiencia: Figura formada por figuras geométricas unidas por yuxtaposición, por la unión de un vértice o por la yuxtaposición parcial de uno de sus lados. Ejemplos: Experiencia para la exploración : Dimensión del proceso en que niñas y niños se enfrentan a una tarea matemática nueva para ellos. Para realizar esta tarea deben adaptar procedimientos ya conocidos para construir un procedimiento que permita resolverla. Experiencia para la consolidación: Dimensión del proceso en que niñas y niños trabajan los conocimien- tos y procedimientos que han surgido, hasta alcanzar un dominio suficiente de los mismos para utilizarlos en otros contextos y en la realización de nuevas tareas. yuxtaposición yuxtaposición parcial unión de un vértice
- 39. 38 Dimensión del procesoen el cual se analiza el trabajo matemático construido por niñas y niños. La eficacia de las técnicas, las justifica- ciones y el logro de los aprendizajes esperados. En los módulos se realiza la evaluación en cada experiencia vivida y al final de todas las experiencias realizadas. Técnica o procedimiento : Manera en que niñas y niños realizan una tarea matemática. Frente a una misma tarea, pueden utilizar distintas técnicas. Una técnica que fue útil para realizar una tarea, puede fracasar si la siguiente tarea está propuesta bajo otras condiciones de realización. Pueden existir distin- tos grados de adecuación de la técnica empleada a la tarea realizada. Hay técnicas más eficaces que otras y, para realizar una tarea matemá- ticabajodeterminadascondiciones,puedeexistirunatécnicaóptima. Elementos que justifican el funcionamiento de las técnicas, explican la adecuación de ellas como herramientas para realizar cierta tarea y establecen relaciones entre las técnicas. Conocimientos matemáticos : Dimensiones de la tarea que permiten variar las condiciones de rea- lización para graduar su complejidad. Al ser modificadas por el pro- fesor, “obligan”al niño a construir un nuevo procedimiento o técnica que se ajuste a las nuevas modificaciones para resolverla. Es en este cambio de las técnicas y de las justificaciones subyacentes, donde se juega la posibilidad del aprendizaje. Estas modificaciones sucesivas permiten a niñas y niños apropiarse del conocimiento matemático involucrado en las tareas en forma amplia e integral. Variable didáctica : Condiciones de realización de la tarea : Al asignar distintos valores a las variables didácticas de una tarea se obtienen distintas condiciones para realizarla. Por ejemplo, si la va- riable didáctica es“tamaño de las colecciones”, los valores que podría adoptar esta variables son“colecciones de hasta 8 objetos”, coleccio- nes de hasta 12 objetos, de hasta 100 objetos, etc. Organización de las tareas en una secuencia en orden creciente de complejidad producido por la modificación sucesiva de las condicio- nes en que hay que realizarlas. Se trata de que niñas y niños vayan elaborando, adaptando y justificando sus procedimientos para poder responder a las exigencias del trabajo propuesto, hasta llegar a en- contrar las técnicas y justificaciones óptimas. Estrategia didáctica : Momento en el cual se identifican y distinguen los conocimientos matemáticos que están detrás de las actividades de aprendizaje rea- lizadas. Se explican y bautizan con el nombre matemático correspon- diente que permita evocarlos con precisión y rapidez. La educadora reorganiza los productos de la actividad de aprendizaje desarrollada, relacionándolos con los conocimientos anteriores. Cierre de las actividades : Experiencia para la evaluación: Es un saber-hacer que organiza una familia de actividades que deben ser realizadas por el alumno para acceder a un aprendizaje esperado específico. Sirve como medio para el aprendizaje, y requiere del uso de un conocimiento matemático. Tarea matemática :
- 40. 39 Apuntes Proyecto LEM-Usach(http://lem.usach.cl), 2006. Bases Curriculares para la Educación Parvularia. Ministerio de Educación (MINEDUC), Chile, 2001. Brousseau Guy. Teoría de las situaciones didácticas. IREM, Strasburg, Francia, 1989. Chamorro, María del Carmen. Didáctica de las matemáti- cas. Colección infantil. Editorial Pearson, Es- paña, 2005. Chevallard Yves. Estudiar matemática: el eslabón perdido entre enseñanza y aprendizaje. SEP México, 1998. Espinoza Salfate, Lorena, González Lasseube, Enrique, Mi- trovich García, Dinko. Unidades Didácticas para el primer ciclo básico. Primer Año Básico, Ministerio de Educación, Chile, 2006. Gálvez, Grecia. El aprendizaje en la orientación en el espacio urbano. Una propuesta para la enseñanza de la geometría en la enseñanza primaria. Cen- tro de investigación del INP, México, 1985. Ruiz Higueras, Luisa. La diferenciación entre la enseñanza de la geometría. Un problema didáctico. Área de Didáctica de la Geometría, Universidad de Jaén. España, 2004. Bibliografía
- 42.
- 44. 43 Descripción de losmateriales a usar en las experiencias Experiencia Materiales para ser gestionados por la educadora Materiales para ser usados por los niños(as) (fichas) Fichas para ser usadas por niños(as) Fichas para ser trabajadas con padres Primera Material 1 y 2 Material 1 y 2 Ficha 4 Segunda Material 2 y 3 Material 2 y 3 Ficha 5 Tercera Material 4 y 5 Material 4 y 5 Ficha 6 Cuarta Material 6 Material 6 Ficha 6 Quinta Material 7 y 8 Material 7 y 8 Ficha 1 Ficha 7 Sexta Material 7 y 8 Material 7 y 8 Ficha 2 Ficha 8 De evaluación de los Aprendizajes Esperados Ficha 3
- 45. 44 Segundo Módulo 2° NT Material 1 Experiencia 1 Modelode configuración
- 46. 45 Segundo Módulo 2° NT Material 2 Experiencia 1 Figurasgeométricas (piezas encajables)
- 47. 46 Segundo Módulo 2° NT Material 3 Experiencia 2 Modelode configuración
- 48. 47 Segundo Módulo 2° NT Material 4 Experiencia 3 Configuraciónde una estrella incompleta
- 49. 48 Segundo Módulo 2° NT Material 5 Experiencia 3 Figurasgeométricas (piezas encajables)
- 50. 49 Segundo Módulo 2° NT Material 6 Experiencia 4 Piezaspara actividad “Armando la cadena”
- 51. 50 Segundo Módulo 2° NT Material6 continuación Experiencia 4 Piezas para actividad “Armando la cadena”
- 52. 51 Segundo Módulo 2° NT Material6 continuación Experiencia 4 Piezas para actividad “Armando la cadena”
- 53. 52 Segundo Módulo 2° NT Material6 continuación Experiencia 4 Piezas para actividad “Armando la cadena”
- 54.
- 55.
- 56. 55 Segundo Módulo 2° NT Ficha 1 Experiencia 5 Nombre: • Instrucción: Marca con una cruz la figura que esá detrás del visor.
- 57. 56 Segundo Módulo 2° NT Ficha 2 Experiencia 5 Dibujala figura • Instrucción: Dibuja la figura oculta detrás del visor. Nombre:
- 58. 57 Segundo Módulo 2° NT Ficha 3 Actividad deevaluación Para evaluar reconocimiento de figuras • Marca la figura que calza en el espacio en blanco. Nombre:
- 59. 58 Segundo Módulo 2° NT Ficha3 continuación Actividad de evaluación Para evaluar reconocimiento de figuras • Marca la figura que está tapada por el cuaderno. Nombre:
- 60. 59 Segundo Módulo 2° NT Ficha 4 Día1 Ficha para ser trabajada en el hogar • Instrucción: Pídale que recorte las figuras y que forme algún objeto conocido. Que le explique què es. Nombre:
- 61. 60 Segundo Módulo 2° NT Ficha 5 Día2 Ficha para ser trabajada en el hogar • Instrucción: Pídale que complete la figura, marcando la línea punteada con un lápiz. Nombre:
- 62. 61 Segundo Módulo 2° NT Ficha 6 Día3 Ficha para ser trabajada en el hogar • Instrucción: Pídale que recorte de revistas o diarios, cuadrados o rectángulos y que luego los pegue en esta ficha. Nombre:
- 63. 62 Segundo Módulo 2° NT Ficha 7 Día4 Ficha para ser trabajada en el hogar • Instrucción: Usando un lápiz, une los extremos de cada una de las figuras. Nombre:
- 64. 63 Segundo Módulo 2° NT Ficha 8 Día5 Ficha para ser trabajada en el hogar • Instrucción: Marca la figura que está oculta detrás del círculo. Nombre: