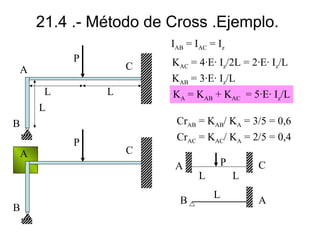
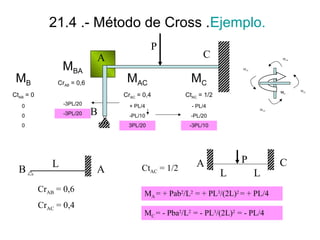
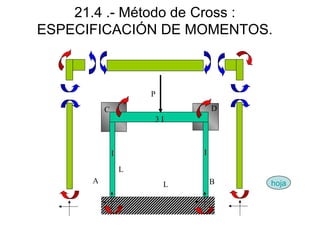
Este documento presenta el método de Cross para analizar nudos rígidos en estructuras. Explica los conceptos clave como nudos no traslacionales, momentos de empotramiento perfecto y reparto de momentos entre barras basado en sus rigideces relativas. También incluye ejemplos numéricos para ilustrar los cálculos de momentos aplicados a cada barra.

1. Universidad Nacional José
Faustino Sánchez Carrión
• METODO DE CROSS.

2. Lección :
• 21.1 .- Rigidez en un extremo apoyado
de una barra. Coeficiente de
transmisión.
• 21.2 .- Rigidez de un nudo.
Coeficientes de reparto o factores de
distribución.
• 21.3 .- Momentos de empotramiento
perfecto.
• 21.4 .- Método de Cross para nudos no
traslacionales. Simplificaciones.
• 21.5 .- Método de Cross para nudos
traslacionales. Simplificaciones.

3. 21.1 .- Rigidez en un extremo apoyado de una barra.
δvb = 0
δhb = 0
δva = 0
MA
φ Flb = 0
B
Rigidez = KAB = MA / φA
Flexibilidad = 1/KAB = φA / MA
fA =0= MA ·L ·L/2EIz - RA·L3/3EIz
φA =MA·L/EIz - RA·L2/2EIz
MA·3/2·L = RA
φA =MA·L/EIz – 3/2·MA·L/2EIz
KAB = MA / φA= 4·E·Iz / L

4. 21.1 .- Coeficiente de transmisión.
δvb = 0
δva = 0
B
MA
KAB = MA / φA= 4·E·Iz/L
δhb = 0
φ Flb = 0
B MB
MA
φA = MA·L/3EIz - MB·L/6EIz
φB = 0 = - MBL/3EIz + MAL/6EIz
MA = 2·MB =>
CtAB = MB/MA= 1/2

5. 21.1 .- Coeficiente de transmisión .
δva = 0
δvb = 0
δhb = 0
B
MA
φA = MA·L/3EIz
KAB = MA / φA= 3·E·Iz/L = 0,75· 4·E·Iz/L
CtAB = MB/MA= 0

6. 21.1 .- Coeficiente de transmisión.
KAB = MA / φA= 4·E·Iz/L
MA
B
MA
B
CtAB = MB/MA= 1/2
KAB = MA / φA= 3·E·Iz/L
CtAB = MB/MA= 0
KAB = MA / φA= 0
CtAB = MB/MA= 0
MA
B

7. 21.2 .- Rigidez de un nudo. Coeficientes de
reparto o factores de distribución.
MB
MB
B
MAB
MAB
E
MAE
C
MA
MAE
MA
MAC
MAD
MAD
D
MA= MAB + MAC + MAD + MAE
MAC

8. 21.2 .- Rigidez de un nudo. Coeficientes de
reparto o factores de distribución.
KAB = MAB / φA= 4·E·Iz/L
MAB
B
MAC
C
CtAB = MB/MAB= 1/2
KAC = MAC/ φA= 3·E·Iz/L
CtAC = MC/MAC= 0
KAD = MAD/ φA= 0
MAD
D
MAE
E
CtAD= MD/MAD= 0
KAE = MAE/ φA= 3·E·Iz/L
CtAE = ME/MAE= 0

9. 21.2 .- Rigidez de un nudo. Coeficientes de
reparto o factores de distribución.
KAB = MAB / φA= 4·E·Iz/L = (4/10)·KA
B
CtAB = MB/MAB= 1/2
C
E
MA
KAC = MAC / φA= 3·E·Iz/L = (3/10)·KA
CtAC = MC/MAC= 0
KAD = MAD / φA= 0 = (0/10)·KA
CtAD = MD/MAD= 0
KAE = MAE / φA= 3·E·Iz/L = (3/10)·KA
D
MA= MAB + MAC + MAD + MAE
CtAE = MC/MAE= 0
MAB= (4/10)·MA
KA = KAB + KAC + KAD + KAE
KA = MA / φA = 4·E·Iz/L + 3·E·Iz/L + 0 + 3·E·Iz/L = 10·E·Iz/L
MB = (2/10)·MA
MAC= (3/10)·MA
MAD= (0/10)·MA
MAE= (3/10)·MA

10. 21.3 .- Momentos de empotramiento
perfecto (no admiten giro)
A
B
L
MA
MB
φB = 0 =q·L3/24EIz - MBL/3EIz - MAL/6EIz
| MB | = | MA | = M =>
q·L3/24EIz = M·L/2EIz
M = q·L2/12
MA = + q·L2/12
MB = - q·L2/12

11. 21.3 .- Momentos de empotramiento
δvb = 0
perfecto (no admiten giro)
δhb = 0
δva = 0
A
P
B
φ Flb = 0
P
B MB
fA = 0 = (P·L/2·L/2·1/2·(2/3·L/2+L/2)-RA·L·L·1/2·2/3·L)/EIz = (5/48·P·L3- 1/3·RAL3)/EIz
5/16·P = RA
MB = -1/2·P·L + RAL = -3/16·P·L
MA = 0

12. 21.3 .- Momentos de empotramiento
perfecto (no admiten giro)
A
B
C
a
L
b
MA
MB
RA
RB
a·RA
ΣMA = 0 = MA + M - MB + RB·L
ΣMC = 0 = MA + M - MB + RB·b - RA·a
b·RB
a·RA
R’A
b·RB
fB = 0 = (RA·a2/2·(b+1/3·a) + RB·b3/3 - MBL2/6 - MAL2/3)/EIz
fA = 0 = (RB·b2/2·(a+1/3·b) + RA·a3/3 - MAL2/6 - MBL2/3)/EIz
φB = 0 = (RA·a2/2 + RB·b2/2 - MBL/2 - MAL/2)/EIz
=>
R’B

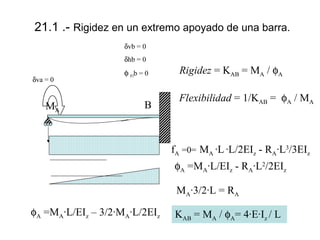
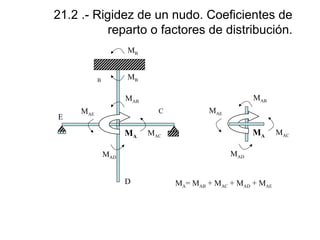
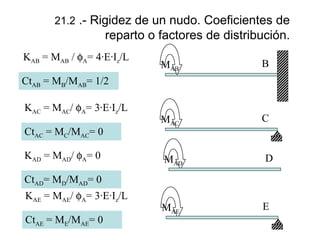
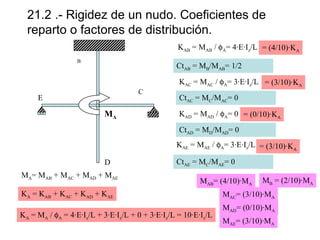
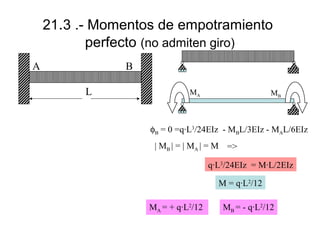
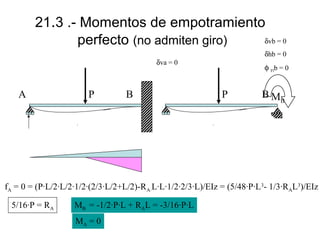
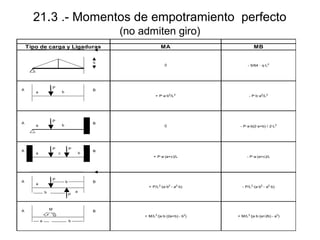
13. 21.3 .- Momentos de empotramiento
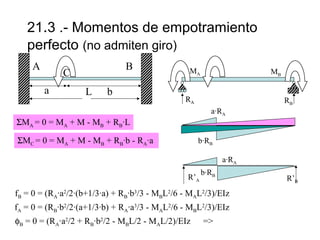
perfecto (no admiten giro)
Tipo de carga y Ligaduras
a
b
- q·L2/8
+ q/L2·[L2·1/2·((a+c)2-a2) - 2/3·L·((a+c)3-a3) + 1/4·(a+c)4-a4)]
- q/L2·[ 1/3·L·((a+c)3-a3) - 1/4·(a+c)4-a4)]
0
c
- q·L2/12
0
b
MB
+ q·L2/12
a
MA
- q/8L2·[a4 -(a+c)4 + 2·L2·c(2·a+c)]
+ q·L2/30
- q·L2/20
0
- q·L2/15
0
- 7·q·L2/120
+ 5/96 · q·L2
- 5/96 · q·L2
c
q
q
q
q

14. 21.3 .- Momentos de empotramiento perfecto
(no admiten giro)
Tipo de carga y Ligaduras
A
A
A
A
P
P
b
c
P
b
b
a
- P·a·b(2·a+b) / 2·L2
- P·a·(a+c)/L
- P/L2·(a·b2 - a2·b)
+ M/L3·[a·b·(a+2b) - a3)
B
B
P
M
A
0
+ P·a·(a+c)/L
B
b
a
- P·b·a2/L2
+ M/L3·[a·b·(2a+b) - b3)
P
a
- 5/64 · q·L2
B
b
a
0
+ P/L2·(a·b2 - a2·b)
P
a
MB
+ P·a·b2/L2
q
MA
a
B
b

15. 21.4 .- Método de Cross
.Introducción.
Objetivo: determinar los momentos que los nudos de una
estructura ejercen sobre las barras. Conocidos estos, puede determinarse
Conocidos estos, puede determinarse
el Diagrama de MF de cada barra,
el Diagrama de MF de cada barra,
supuesta apoyada en sus extremos.
supuesta apoyada en sus extremos.
Tipos de nudos rígidos:
•Inamovibles o absolutamente fijos (fv, fh y φ nulos)
•No traslacionales (fv, fh nulos, pero pueden girar)
•Traslacionales: permiten desplazarse y girar.
Las deformaciones debidas aaesfuerzos Normales yyCortantes se
Las deformaciones debidas esfuerzos Normales Cortantes se
suelen despreciar frente aalas de Flexión.
suelen despreciar frente las de Flexión.

16. 21.4 .- Método de Cross .Etapas.
Se usa en nudos no traslacionales
1.- Cálculo de los momentos de empotramiento perfecto (como
si los nudos fuesen absolutamente fijos)
2.- Equilibrado de los nudos, repartiendo el momento de
equilibrado entre las barras concurrentes proporcionalmente
a sus rigideces.

17. 21.4 .- Método de Cross .Ejemplo.
IAB = IAC = Iz
P
A
L
L
C
L
KAC = 4·E· Iz/2L = 2·E· Iz/L
KAB = 3·E· Iz/L
KA = KAB + KAC = 5·E· Iz/L
CrAB = KAB/ KA = 3/5 = 0,6
B
A
P
C
CrAC = KAC/ KA = 2/5 = 0,4
A
B
B
P
L
L
L
C
A

18. 21.4 .- Método de Cross .Ejemplo.
MB
MBA
A
C
MAC
-3PL/20
0
-3PL/20
B
0
L
CrAB = 0,6
CrAC = 0,4
A
+ PL/4
- PL/4
-PL/10
MAE
CtAC = 1/2
-PL/20
3PL/20
0
MAB
MC
CrAC = 0,4
CrAB = 0,6
CtAB = 0
B
P
-3PL/10
CtAC = 1/2
A
MA
MAD
P
L
L
MA = + Pab2/L2 = + PL3/(2L)2 = + PL/4
MC = - Pba2/L2 = - PL3/(2L)2 = - PL/4
C
MAC

19. 21.4 .- Método de Cross :
ESPECIFICACIÓN DE MOMENTOS.
P
D
C
3I
I
I
L
A
L
B
hoja