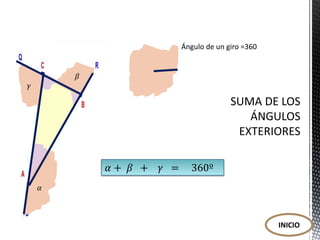
El documento aborda temas fundamentales sobre triángulos, incluyendo su definición, elementos, clasificación, propiedades y la relación entre lados y ángulos. Se detalla la suma de los ángulos interiores y exteriores de los triángulos, así como se presentan ejercicios para calcular ángulos. Además, se clasifican los triángulos según sus lados y ángulos, destacando características y relaciones clave entre ellos.

2. DEFINICIÓN
ELEMETOS DE UN TRIÁNGULO
PROPIEDAD TRIANGULAR
CLASIFICACIÓN DE TRIÁNGULOS
RELACIÓN ENTRE LADOS Y ÁNGULOS
SUMA DE LOS ÁGULO INTERIORES
SUMA DE LOS ÁNGULOS EXTERIORES
EJERCICIOS

3. Completa las definiciones
 Se llama triángulo a todo
polígono de ……... lados
Los triángulos se determinan
como intersección
de …………semiplanos
3 (TRES)
3 (TRES)
INICIO

4. • VERTICE : A B C
• LADOS: 𝐴𝐵 𝐵𝐶 𝐶𝐴
• ÁNGULOS
INRERIORES: 𝐴 𝐵 𝐶
• ÁNGULOS
EXTERIORES: 𝛼 𝛽 𝛾
𝛾
𝛽
𝛼
INICIO

5. A
B
C
𝐶𝐴𝐵𝐶
𝐵𝐶 + 𝐶𝐴
𝐴𝐵
𝐶𝐴 − 𝐵𝐶
𝐵𝐶
𝐶𝐴
INICIO
𝐶𝐴 − 𝐵𝐶 < 𝐴𝐵 < 𝐵𝐶 + 𝐶𝐴

6. SUMA DE LOS ÁNGULOS INTERIORE
DE UN TRIÁNGULO
Dado el triángulo ABC
Los ángulos interiores son 𝐴 𝐵 Y 𝐶
Si se disponen los tres ángulos en forma consecutiva
Así se forma un ángulo llano
Pol tanto 𝑨 + 𝑩 + 𝑪 = 180º
INICIO

7. INICIO

8. • A lados iguales se oponen ángulos lados iguales
• Al mayor de los lados se
opone el mayor de sus ángulos
• En el triángulo rectángulo el mayor
de sus lados se llama HIPOTENUSA y
los otros dos CATETOS
INICIO

9. 𝛾
𝛼
Ángulo de un giro =360
𝛼 + 𝛽 + 𝛾 = 360º
𝛽
INICIO

10. Cuando se forma triángulo
Ejercicios con ayuda
completa teniendo en cuenta las características de los
triángulos
Plantea y resuelve ecuaciones par calcular los ángulos
Resolución
INICIO

11. AB BC A𝐶 Verifico o no la propiedad Construcción del ABC
5cm 4cm 3cm
6cm 10cm 6cm
7cm 2cm 5cm
5cm 9cm 2cm
INICIO

12. 52º22º
x
85º
26º
x
108º
64º
43º
66º
22º + 52º + x = 180º
64º + 85º + x = 180º
26º + 108º + x = 180º
66º + x + 43º = 180º
x
x INICIO

13. Triángulos
Clasificación
según los lados
Clasificación
según los
ángulos
Igualdad de
lados y de
ángulos
Valor de los
ángulos
indicados
Dos lados y dos
ángulos
iguales
Tres lados y tres
ángulos iguales
Isósceles
Isósceles Rectángulo
𝐶=65ºA
B
A
B
B
C
𝐶=36º
B
A
A
B
C
𝐶=100º
INICIO

14. x + 4x + 4x = 180º
9x = 180º
x = 180º : 9
𝑎 = 𝑥 = 20º
𝑏 = 4𝑥 = 4.20º
𝑏 = 𝑐 = 80º
INICIO

15. Cuando se forma triángulo
Ejercicios con ayuda
completa teniendo en cuenta las características de los
triángulos
Plantea y resuelve ecuaciones par calcular los ángulos

16. 52º22º
x
85º
26º
x
108º
64º
43º
66º
22º + 52º + x = 180º
64º + 85º + x = 180º
26º + 108º + x = 180º
66º + x + 43º = 180º
x
x INICIO
74º + x = 180º
x = 180º - 74º
x = 106º
x = 180º - (64º + 85º )
x = 180º - 149º
x = 31º
114º + x = 180º
x = 180º - 114º
x = 66º
x = 180º - 109º
x = 180º - 43º - 66º
x = 71º

17. Triángulos
Clasificación
según los lados
Clasificación
según los
ángulos
Igualdad de
lados y de
ángulos
Valor de los
ángulos
indicados
Dos lados y dos
ángulos
iguales
Tres lados y tres
ángulos iguales
Isósceles
Isósceles Rectángulo
𝐶=65ºA
B
A
B
B
C
𝐶=36º
B
A
A
B
C
𝐶=100º
INICIO
isósceles
𝐴 = 𝐶 = 65
65º + 𝐵 + 65º = 180º
𝐵 = 180º − 130º
𝐵 = 50º
acutángulo
equilátero
𝐴 = 𝐵 = 𝐶 = 𝑥
𝑥 + 𝑥 + 𝑥 = 180º
3𝑥 = 180º
𝑥 = 180º: 3 = 60º
acutángulo
rectángulo
𝐴 = 90º
90º + 𝐵 + 36º = 180º
𝐵 = 180º − 126º
𝐵 = 54º
escaleno

18. INICIO
x + 4x + 4x = 180º
9x = 180º
x = 180º : 9
𝑎 = 𝑥 = 20º
𝑏 = 4𝑥 = 4.20º
𝑏 = 𝑐 = 80º
3x + 90ª + 2x -15º= 180º
5x = 180º - 90º +15
x = 105º : 5
𝑥 = 20º
𝑥 = 21º
𝑎 = 3.21º
𝑎 =63º
𝑐 = 2.21º-15º
𝑐 = 26º
2x +25º+ 90ª + 3x -5º= 180º
5x +105º = 180º
5x = 180º -105º
5x = 75º
x = 75º:5
x = 25º