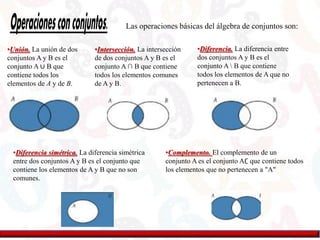
Este documento define conjuntos y números reales, y describe las operaciones básicas de álgebra de conjuntos como unión, intersección, diferencia y complemento. También explica desigualdades matemáticas, incluyendo signos de desigualdad, valor absoluto y cómo resolver desigualdades de valor absoluto considerando casos positivos y negativos.

1. República Bolivariana de Venezuela
Ministerio del Poder Popular para la Educación Universitaria
Universidad Politécnica Territorial “Andrés Eloy Blanco”
Barquisimeto, Estado Lara
BARQUISIMETO, MARZO 2021
Autor:
Yilbert Colmenares
CI: V-27.666.483
PNF CONTADURIA
Sección 0407

2.  Definición de Conjuntos. Un conjunto es la
agrupación de diferentes elementos que
comparten entre sí características y
propiedades semejantes. Estos elementos
pueden ser sujetos u objetos, tales
como números, canciones, meses, personas,
etc. Por ejemplo: el conjunto de números
primos o el conjunto de planetas del sistema
solar.
Conjunto numérico. Agrupación de números
mediante una serie de propiedades
estructuradas.
 En matemáticas, un conjunto es una
colección de elementos con características
similares considerada en sí misma como un
objeto. Los elementos de un conjunto,
pueden ser las siguientes: personas,
números, colores, letras, figuras, etc.

3. •Unión. La unión de dos
conjuntos A y B es el
conjunto A ∪ B que
contiene todos los
elementos de A y de B.
Las operaciones básicas del álgebra de conjuntos son:
•Intersección. La intersección
de dos conjuntos A y B es el
conjunto A ∩ B que contiene
todos los elementos comunes
de A y B.
•Diferencia. La diferencia entre
dos conjuntos A y B es el
conjunto A B que contiene
todos los elementos de A que no
pertenecen a B.
•Diferencia simétrica. La diferencia simétrica
entre dos conjuntos A y B es el conjunto que
contiene los elementos de A y B que no son
comunes.
•Complemento. El complemento de un
conjunto A es el conjunto A∁ que contiene todos
los elementos que no pertenecen a "A"

4. Números Reales.
Se puede definir a los números reales como aquellos números que
tienen expansión decimal periódica o tienen expansión decimal no
periódica. Por ejemplo
a) 3 es un número real ya que 3 = 3,00000000000….
b) ½ es un número real ya que ½ = 0,5000000000….
c) 1/3 es un número real ya que 1/3 = 0,3333333333333….
d) 2es un número real ya que 2=
1,4142135623730950488016887242097….
e) 0,1234567891011121314151617181920212223….
f) 1,01001000100001000001000000100000001….
g) π
PROPIEDADES DE LOS NÚMEROS
REALES:
Propiedad: Conmutativa
Operación: Suma y Resta
Definición: a+b = b+a
Que dice:
El orden de sumar o multiplicar no afecta el
resultado
Ejemplo:
2+8 = 8+2 5(-3) = (-3)5

5. Conjunto de los números Reales
De acuerdo a lo anteriormente expuesto, el conjunto de los números reales se define como la unión de dos tipos de
números, a saber; los números racionales, los números irracionales .A su vez, los números racionales se clasifican
en:
a)Números Naturales (N)
los que usamos para contar. Por ejemplo, 1, 2, 3, 4, 5,6, 7, 8, 9, 10, 11, …
b)Números Enteros (Z)
son los números naturales, sus negativos y el cero. Por ejemplo: -3, -2, -1, 0, 1, 2, 3,…
c)Números Fraccionarios
son aquellos números que se pueden expresar como cociente de dos números enteros, es decir, son números de la
forma
a/b con a, b enteros y b ≠ 0.
d)Números Algebraicos
son aquellos que provienen de la solución de alguna ecuación algebraica y se representan por un número finito de
radicales libres o anidados. Por ejemplo, √3ª
e)Números Trascendentales: No pueden representarse mediante un número finito de raíces libres o anidadas;
provienen de las llamadas funciones trascendentes :trigonométricas, logarítmicas y exponenciales.

6. Desigualdades.
La desigualdad matemática es aquella
proposición que relaciona dos expresiones
algebraicas cuyos valores son distintos. Se trata
de una proposición de relación entre dos
elementos diferentes, ya sea por desigualdad
mayor, menor, mayor o igual, o bien menor o
igual. Cada una de las distintas tipologías de
desigualdad debe ser expresada con diferente
signo (> o <, etcétera) y tendrá una reacción a
operaciones matemáticas diferente según su
naturaleza.
Por lo tanto, si queremos explicar cuál es la
finalidad de este concepto con el menor número
de palabras posibles diremos que; el objetivo de
la desigualdad matemática es mostrar que dos
sujetos matemáticos expresan valores
diferentes.

7. Ejemplo
Valor
Valor
Absoluto
5 5
-5 5
Signos de desigualdad matemática.
Podemos sintetizar los signos de expresión de
todas las desigualdades matemáticas posibles en
los cinco siguientes:
•Desigual a: ≠
•Menor que: <
•Menor o igual que: ≤
•Mayor que: >
•Mayor o igual que: ≥
Cada una de ellas debe relacionar dos elementos
matemáticos. De modo que implicaría que a es
menor a b, mientras que “a>b” significa que a es
mayor a b. En el caso de “a≠b”, leeremos la
expresión como a es desigual a b, “a≤b”; a es
menor o igual a b, y “a≥b” implica que a es mayor
o igual a b.
Es también importante conocer que la expresión
de desigualdad matemática “a≠b” no es
excluyente con las expresiones “a” y “a>b”, de
modo que, por ejemplo, “a≠b” y “a>b” pueden ser
ciertas al mismo tiempo. Por otro lado, tampoco
son excluyentes entre sí las expresiones “a≥b” y
“a>b” o “a≤b” y “a”.
Ejemplos.
Las desigualdades matemáticas están formadas,
en la mayoría de ocasiones, por dos miembros
o componentes. Un miembro se encontrará a la
izquierda del símbolo y el otro a la derecha.
Un ejemplo sería expresar: 4x – 2 > 9. Lo
leeríamos diciendo que “cuatro veces nuestra
incógnita menos dos es superior a nueve”.
Siendo el elemento 4x-2 el elemento A y 9 el
elemento B. La resolución nos mostraría que
(en números naturales) la desigualdad se
cumple si x es igual o superior a 3 (x≥3).

8. Tipología de desigualdades.
 Existen dos tipos distintos de desigualdades dependiendo de su nivel de aceptación. Ninguna de
ellas no incluye la desigualdad general (≠). Son las siguientes:
•Desigualdades estrictas: son aquellas que no aceptan la igualdad entre elementos. De este modo,
entenderemos como desigualdades de este tipo el “mayor que” (>) o “menor que” (<).
•Desigualdades amplias o no estrictas: todas aquellas en las que no se especifica si uno de los
elementos es mayor/menor o igual. Por lo tanto, estamos hablando de “menor o igual que” (≤), o
bien “mayor o igual que” (≥).
Definición de Valor Absoluto
El valor absoluto puede ser explorado ya sea numérica o gráficamente. Numéricamente, el valor
absoluto se indica encerrando el número, variable o expresión dentro de barras verticales, así:
|20|
|x|
|4n − 9|
 Cuando tomamos el valor absoluto de un número, éste es siempre positivo o cero. Si el valor
original ya es positivo o cero, el valor absoluto es el mismo. Si el valor original es negativo,
simplemente nos deshacemos del signo. Por ejemplo, el valor absoluto de 5 es 5. El valor
absoluto de -5 es también 5.

9. Desigualdades de valor absoluto
Una desigualdad de valor absoluto es una desigualdad que tiene un signo de valor absoluto con una
variable dentro.
Desigualdades de valor absoluto (<):
La desigualdad | x | < 4 significa que la distancia entre x y 0 es menor que 4.
Así, x > -4 Y x < 4. El conjunto solución es
Cuando se resuelven desigualdes de valor absoluto, hay dos casos a considerar.
 Caso 1: La expresión dentro de los símbolos de valor absoluto es positiva.
 Caso 2: La expresión dentro de los símbolos de valor absoluto es negativa.
La solución es la intersección de las soluciones de estos dos casos.
En otras palabras, para cualesquiera números reales a y b , si | a | < b , entonces a < b Y a > - b .