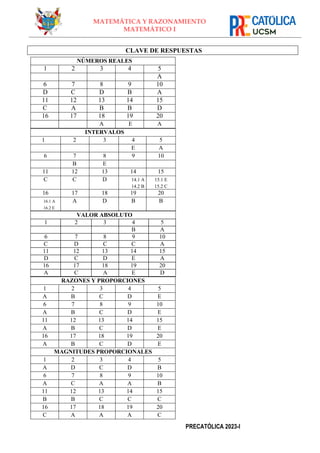
Este documento presenta una introducción a los números reales. Define los números reales como cualquier número que se encuentre en la recta numérica real, la cual incluye números racionales e irracionales. Explica las principales características de los números reales como su orden, integralidad y capacidad de ser expresados como decimales infinitos. Además, describe los conjuntos de números naturales, enteros, racionales e irracionales y cómo estos se incluyen dentro del conjunto de los números reales.







![7 PRECATÓLICA 2023-I
MATEMÁTICA Y RAZONAMIENTO
MATEMÁTICO I
PRACTIQUEMOS N°1
1. Completa el cuadro
PRODUCTOS POTENCIA BASE EXPONENTE
2.2.2.2.2
5.5.5.5.5.5
7.7.7
10.10.10.10
8.8.8.8.8.8.8
4.4.4.4
12.12.12.12
20.20.20.20.20
4.4.4.4.4.4.4
17.17
2. Efectúa las siguientes operaciones
aplicando las propiedades de la
potenciación.
a. 45÷
43
b. 106
÷ 103
c.103
× 106
× 100
d.(57
. 53
). 54
e.( (26
. 27
) ÷ (22
. 28
)
f.167
÷ 167
g. [(53
)2]0
3. Resuelve aplicando las propiedades
a. √4 900
b.√640 000
c. √90 000
d. √810 000
4
e. √3 200 000
5
4. Calcula el valor de cada raíz aplicando las
propiedades
a. √√81√16
b. √√√256
c. √169 +√64.27
3
d. √√729
3
e. √
2 500
1 600](https://image.slidesharecdn.com/mat-221112140247-8b91aa08/85/MAT-Y-RAZ-MATEMATICO-I-2023-I-pdf-8-320.jpg)

![9 PRECATÓLICA 2023-I
MATEMÁTICA Y RAZONAMIENTO
MATEMÁTICO I
9. La diferencia de los cubos de dos números
impares consecutivos es 602.El valor de su
suma es :
A)21 B) 20 C) 27 D) 22 E) 29
10. El cociente del cuadrado de un número entero
menos 45 entre la raíz cuadrada de la
diferencia del cuadrado del número
mencionado y 72 es 12. El valor del número
es :
A)9 B)4 C) 6 D) 5 E)2
11. Calcular un número cuyo cuadrado
disminuido en 119 es igual a 10 veces el
exceso del número con respecto a 3.
A)12 B) 11 C) 13 D )14 E)15
12. Resolver:
[√(
1
2
)
−3
+ (
4
3
)
−1
+ 2−2 ]
3
√√324
4
A) 1 B)2 C)4 D) 6 E)8](https://image.slidesharecdn.com/mat-221112140247-8b91aa08/85/MAT-Y-RAZ-MATEMATICO-I-2023-I-pdf-10-320.jpg)


![12 PRECATÓLICA 2023-I
MATEMÁTICA Y RAZONAMIENTO
MATEMÁTICO I
Un subconjunto de la recta real se llama intervalo, y
contiene a todos los números reales que están
comprendidos entre dos cualquiera de sus elementos.
Geométricamente los intervalos corresponden a
segmentos de recta, semirrectas o la misma recta real.
Los intervalos de números correspondientes a
segmentos de recta son intervalos finitos, los intervalos
correspondientes a semirrectas y a la recta real son
intervalos infinitos
Los intervalos finitos pueden ser cerrados, abiertos o
semiabiertos
1. Representación de intervalos
¿Cómo se representará un intervalo que contiene
infinitos números? Pues con infinitos puntos, es decir,
dibujando el tramo de la recta real que representa ha
dicho intervalo. Vamos a verlo a continuación.
2. Operaciones con intervalos
Los intervalos son conjuntos de números reales, por lo
tanto, se pueden realizar las operaciones definidas entre
conjuntos: unión, intersección, diferencia, diferencia
simétrica y complemento. Para los conjuntos definidos
como intervalos, el conjunto universal o de referencia
U es el conjunto de los números reales R.
Cualquier subintervalo se denota por una letra
mayúscula. Si A está contenido en los números reales,
gráficamente, se puede representar de la siguiente
manera:
El intervalo A = [a,b] = {x ∈ R/a ≤ x ≤ b}, es un
subconjunto de números reales y en la recta real se
representa de la siguiente forma:
2.1 Unión de intervalos
La unión entre los conjuntos A y B se define como
A ∪ B = {x/x ∈ A ∨ x ∈ B}.
El conjunto A ∪ B está formado por todos los
elementos que pertenecen a A o pertenecen a B sin
repetirlos.
En la unión de dos conjuntos A y B se pueden presentar
tres situaciones: A y B no tienen elementos en común,
como se muestra en la siguiente figura.
A∪B, si A y B no tienen elementos en común
Los intervalos A = (−3,0] y B = [1,2), no tienen
elementos en común. Gráficamente se representan de
la siguiente manera:
Para los intervalos A y B, A∪B = (−3,0] ∪ [1,2) se
representa gráficamente como sigue:
A y B tienen elementos en común.](https://image.slidesharecdn.com/mat-221112140247-8b91aa08/85/MAT-Y-RAZ-MATEMATICO-I-2023-I-pdf-13-320.jpg)
![13
MATEMÁTICA Y RAZONAMIENTO
MATEMÁTICO I
A∪B, si A y B tienen elementos en común.
Ejemplo: Los intervalos A = (−3,0] y B = (−1,2), tienen
al intervalo (−1,0] en común. Gráficamente se
representan de la siguiente manera:
La unión A∪B = (−3,0] ∪ (−1,2) = (−3,2), que se
representa gráficamente como sigue:
Uno de los dos conjuntos está totalmente
contenido en el otro. En la figura siguiente, el
conjunto B, es totalmente contenido en el A.
A∪B, si B está totalmente contenido en A
Ejemplo Los intervalos A = (−3,0] y B = [−2, −1].
El intervalo B, está totalmente contenido en el
intervalo A. gráficamente se representan de la
siguiente manera:
La unión A∪B = (−3,0] ∪ [−2, −1] = (−3,0], que se
representa gráficamente como sigue:
2.2 Intersección de intervalos
La intersección entre los conjuntos A y B se define
como:
A∩B = {x/x ∈ A ∧ x ∈ B}
El conjunto A∩B está formado por todos los elementos
comunes entre los dos conjuntos sin repetirlos. En
general, en la intersección de dos conjuntos A y B se
pueden considerar tres situaciones: A y B no tienen
elementos en común, como se muestra en la siguiente
figura.
Ejemplo: Los intervalos A = (−3,0] y B = [1,2), no
tienen elementos en común.
Gráficamente se representan de la siguiente manera:
A∩B, si A y B no tienen elementos en común.
La intersección A∩B = (−3,0] ∩ [1,2) = ∅ (conjunto
vacío), que no tiene una representación gráfica en la
recta real.
Al efectuar la unión entre conjuntos, los
elementos en común no se repiten.](https://image.slidesharecdn.com/mat-221112140247-8b91aa08/85/MAT-Y-RAZ-MATEMATICO-I-2023-I-pdf-14-320.jpg)
![14
MATEMÁTICA Y RAZONAMIENTO
MATEMÁTICO I
A y B tienen elementos en común.
A∩B, si A y B tienen elementos en común.
Los intervalos A = (−3,0] y B = (−1,2), tienen al
intervalo (−1,0] en común. Estos elementos, son la
intersección de los dos conjuntos.
La intersección A∩B = (−3,0] ∩ (−1,2) = (−1,0], se
representa gráficamente como sigue:
El elemento −1 ∈ A, pero −1 ∉ B, por lo tanto
−1 ∉ A∩B.
Uno de los dos conjuntos está totalmente contenido en
el otro. En la figura siguiente, el conjunto B, está
totalmente contenido en el A.
A∩B = B, si B está contenido en A,
Ejemplo Para los intervalos A = (−3,0] y
B = [−2, −1], el intervalo B, está totalmente contenido
en el intervalo A. Gráficamente se representan de la
siguiente manera:
En la intersección A∩B = (−3,0] ∩ [−2, −1] = B, los
elementos que están en la intersección son todos los de
B.
2.3 Diferencia de intervalos
La diferencia entre los conjuntos A y B se define como:
A−B = {x/x ∈ A∧x ∈/ B}.
El conjunto A−B está formado por todos los elementos
que pertenecen a A y no pertenecen a B.
Ejemplo: Los intervalos A = (−3,0] y B = [1,2), no
tienen elementos en común. Gráficamente, la
diferencia, se representan de la siguiente manera:
A−B = A, si A y B no tienen elementos en común
La diferencia A−B = (−3,0] − [1,2) = A.
En este caso, todos los elementos de B no están en A.
A y B tienen elementos en común.
B−A, si A y B tienen elementos en común.
Ejemplo Los intervalos A = (−3,0] y B = (−1,2), tienen
al intervalo (−1,0] en común. Gráficamente se
representan de la siguiente manera:
Para que un elemento esté en la intersección,
debe pertenecer a ambos intervalos.](https://image.slidesharecdn.com/mat-221112140247-8b91aa08/85/MAT-Y-RAZ-MATEMATICO-I-2023-I-pdf-15-320.jpg)
![15
MATEMÁTICA Y RAZONAMIENTO
MATEMÁTICO I
La diferencia A−B = (−3,0] − (−1,2) = (−3, −1], que se
representa gráficamente como sigue:
Observe que −1 ∈ A y −1 ∉ B, por lo tanto
−1 ∈ A−B. Uno de los dos conjuntos está totalmente
contenido en el otro.
En la figura siguiente, el conjunto B, está totalmente
contenido en el A.
B−A, si A y B tienen elementos en común.
Ejemplo Los intervalos A = (−3,0] y B = [−2, −1]. El
intervalo B, está totalmente contenido en el intervalo
A. Gráficamente se representan de la siguiente manera:
La diferencia
A−B = (−3,0] − [−2, −1] = (−3, −2) ∪ (−1,0], que se
representa gráficamente como sigue:
Observe que los elementos que pertenecen a los dos
intervalos no están en la diferencia
Para los intervalos A = (−3,0] y B = (−1,2) se tiene que
A−B = (−3, −1] y B−A = (0,2).
Gráficamente estos dos últimos intervalos se
representan de la siguiente manera:
2.4 Complemento de un conjunto
El complemento de un conjunto A,
A ′ = 𝐴𝑐
= {x/x ∉ A}, en palabras, se define como el
conjunto de todos los elementos que no están en A ó lo
que le falta a A para ser igual al universal.
El complemento de un intervalo A = [a, b], es
A ′ = (−∞, a) ∪ (b, ∞). Son todos los números reales
que no pertenecen a. Se representa en la recta real de la
siguiente manera:
Complemento del intervalo [a,b],
A ′ = (−∞,a)∪(b,∞)
Note que si a ∈ A, a ∉ A’, si b ∈ A, b ∉ A’. El
complemento de un intervalo B = (a,b), es
B’ = (−∞,a]∪[b,∞). Son todos los números reales que
no pertenecen a B. Se representa en la recta real de la
siguiente manera:
La diferencia entre intervalos no es
conmutativa, es decir A−B ≠B−A.
El complemento del conjunto A, son todos los
elementos que están por fuera de A.](https://image.slidesharecdn.com/mat-221112140247-8b91aa08/85/MAT-Y-RAZ-MATEMATICO-I-2023-I-pdf-16-320.jpg)
![16
MATEMÁTICA Y RAZONAMIENTO
MATEMÁTICO I
Complemento del intervalo (a,b) es
B ′ = (−∞,a]∪[b,∞).
Note que si a ∉ B, a ∈ B ′ , si b ∉ B, b ∈ B ′ .
Ejemplo Encontrar y graficar los complementos de los
intervalos A = [3,5] y B = [−2,3). Para el conjunto A,
su complemento es
A ′ = (−∞,3)∪(5,∞). Gráficamente, se representa de la
siguiente manera: Para el intervalo B, su complemento
es
B ′ = (−∞,−2)∪[3,∞) y gráficamente se representa por:](https://image.slidesharecdn.com/mat-221112140247-8b91aa08/85/MAT-Y-RAZ-MATEMATICO-I-2023-I-pdf-17-320.jpg)
![17
MATEMÁTICA Y RAZONAMIENTO
MATEMÁTICO I
PRACTIQUEMOS
1. Completa el siguiente cuadro
REPRESNTACIÓN
SIMBÓLICA
REPRESENTACIÓN
CONJUNTISTA
[𝟐; 𝟓]
{𝐱/𝐱 ∈ ℝ ∧ −𝟐 < 𝐱 ≤ 𝟓}
〈−𝟗; 𝟐〉
{𝐱/𝐱 ∈ ℝ ∧ −𝟑 ≤ 𝐱 < 𝟔}
[𝟑; +∞⟩
[−𝟓; 𝟒⟩
2. Realiza la representación gráfica de:
a) {𝐱/𝐱 ∈ ℝ ∧ −𝟏 ≤ 𝐱 ≤ 𝟒}
b){𝐱/𝐱 ∈ ℝ ∧ 𝐱 > −𝟒}
c){𝐱/𝐱 ∈ ℝ ∧ 𝐱 ≤ 𝟔}
d){𝐱/𝐱 ∈ ℝ ∧ −𝟏 < 𝐱 ≤ 𝟐}
3. Dado los conjuntos:
E = {x/x ∈ ℝ ∧ −4 < x ≤ 7}
F = {x/x ∈ ℝ ∧ −5 ≤ x < 8}
G = {x/x ∈ ℝ ∧ −3 ≤ x ≤ 6}
Graficar y dar respuesta a la siguiente
operación.
a) 𝐸 ∪ 𝐹
b) F ∪ G
c)𝐸 ∪ 𝐺
4. Con los datos del ejercicio anterior , graficar y
dar respuesta a la siguiente operación
𝐸 ∪ 𝐹 ∪ 𝐺
A)
[2; 5]
B)
[5; 8⟩
C)
〈−4; 2〉
D)
⟨−3; 6]
E)
[−5; 8⟩](https://image.slidesharecdn.com/mat-221112140247-8b91aa08/85/MAT-Y-RAZ-MATEMATICO-I-2023-I-pdf-18-320.jpg)
![18
MATEMÁTICA Y RAZONAMIENTO
MATEMÁTICO I
5. A un bingo asistieron personas de
diferentes edades marcando un orden de
llegada al evento de esta manera: en primer
lugar de 12 a 20 años, en el segundo lugar
de 17 a 24 años y en tercer lugar de 15 a 29
años ¿En qué intervalo de edades se
encontraban todas las personas que
asistieron?
A)
[𝟏𝟐; 𝟐𝟗]
B)
[𝟏𝟓; 𝟏𝟖⟩
C)
〈𝟏𝟒; 𝟐𝟗〉
D)
⟨𝟏𝟑; 𝟏𝟔]
E)
[𝟏𝟐;𝟐𝟒⟩
6. Dado los conjuntos:
𝐌 = {𝒙/𝒙 ∈ ℝ ∧ −𝟏 < 𝒙 < 𝟗}
𝐍 = {𝐱/𝐱 ∈ ℝ ∧ −𝟑 ≤ 𝐱 ≤ 𝟔}
𝐏 = {𝒙/𝒙 ∈ ℝ ∧ −𝟐 ≤ 𝒙 < 𝟖}
Graficar y dar respuesta en intervalos:
𝑎) 𝑀 ∩ 𝑁
𝑎) 𝑀 ∩ 𝑃
𝑎) 𝑁 ∩ 𝑃
7. Con los datos del ejercicio anterior ,
graficar y dar respuesta a la siguiente
operación
𝑀 ∩ 𝑁 ∩ 𝑃
A)
B)
A)
〈−𝟐; 𝟓〉
B)
⟨−𝟏; 𝟔]
C)
[−𝟐; 𝟖]
D)
[−𝟑; 𝟗]
C) E)
D) 〈𝟓; 𝟔〉
A) ⟨−𝟐; −𝟏]
8. Marita por la pandemia tiene las sesiones
sincrónicas de Matemática de 8:00 a 11:00, Lucho
de 9:00 a 12:00 y Toño de 9:00 a 13:00 ¿En qué
intervalo de tiempo se encontrarán los tres en la
clase de Matemática?
A) 〈8: 00; 10: 00〉
B) 〈9: 00; 12:00〉
C) [10: 00; 11: 00]
D) [8: 00; 10: 00]
E) 〈9: 00; 11:00〉](https://image.slidesharecdn.com/mat-221112140247-8b91aa08/85/MAT-Y-RAZ-MATEMATICO-I-2023-I-pdf-19-320.jpg)
![19
MATEMÁTICA Y RAZONAMIENTO
MATEMÁTICO I
9. Dado los conjuntos:
M = {x/x ∈ ℝ ∧ 5 < x < 9}
E = {x/x ∈ ℝ ∧ −1 < x ≤ 6}
G = {x/x ∈ ℝ ∧ −4 ≤ x ≤ 8}
Graficar y dar respuesta a la siguiente operación.
𝐴) 𝑀 − 𝐸
𝐵) 𝐸 − 𝐺
𝐶) 𝑀 − 𝐺
10. Considerando el ejercicio anterior resolver:
𝐴) 𝐸 − 𝑀
𝐵) 𝐺 − 𝐸
𝐶) 𝐺 − 𝑀
11. ¿Entre qué edades coinciden tres grupos de
personas que se presentan a una convocatoria de
audición para un musical : cantantes, músicos y
sonidistas?, sus edades respectivamente
son: [15; 23]; [17; 35] 𝑦 ⟨16; 34] ? (edades
expresadas en intervalos)
A)
〈14; 35〉
B)
⟨12;34]
C)
[17; 23]
D)
[15; 34]
E) E)
F) 〈15; 36〉
12. Los alumnos de un colegio deben trazar una
recta numérica de números reales en su
cuaderno. Un alumno dibuja del punto -3 al
punto 9, su amigo del punto 0 al punto 9 y otro
del punto -7 al punto 6 ¿Cuál es el trazo que
realizaron los tres a la ves?
A)
〈−1; 5〉
B)
⟨−2;4]
C)
[0; 6]
D)
[−3; 0]
G) E)
H) 〈−7; 9〉](https://image.slidesharecdn.com/mat-221112140247-8b91aa08/85/MAT-Y-RAZ-MATEMATICO-I-2023-I-pdf-20-320.jpg)
![20
MATEMÁTICA Y RAZONAMIENTO
MATEMÁTICO I
13. José llega al gimnasio a las 10 horas y estuvo
3 horas, Edgar llega a las 12 horas estando 2
horas , Amalia llegó a las 11 horas y estuvo 4
horas ¿ En qué intervalo coincidieron las tres
personas en el gimnasio ?
A)
⟨𝟏𝟐; 𝟏𝟕]
B)
[𝟏𝟓; 𝟏𝟗⟩
𝑪)
⟨𝟏𝟑;𝟐𝟑⟩
D)
[𝟏𝟐; 𝟏𝟑]
E)
〈𝟏𝟐; 𝟏𝟒〉
14. Graficar y dar respuesta a las siguiente
operaciones de complemento de intervalos
14.1. M’
M = ⟨−3; 6]
A) ⟨−∞; −3] ∪ ⟨6; +∞⟩
B) ⟨−∞; 3] ∪ [5; +∞⟩
C) 〈−∞; +∞〉
D) ⟨−3; 5] ∪ 〈−∞; +∞〉
E) ∅
14.2. G’
G= 〈5; 9〉
A)⟨−∞; 2] ∪ [8; +∞⟩
B)⟨−∞; 5] ∪ [9; +∞⟩
C) ∅
D) 〈−∞; +∞〉
E) ⟨−2; −4] ∪ 〈−∞; +∞〉
15. Para el mundial de Futbol en Qatar se han
realizado mediciones de temperatura en dos
estadios para un mejor desarrollo del torneo,
las temperaturas se han medido en intervalos
las cuales son :
𝐴 = [23°;35°] 𝐵 = ⟨20°; 32°]
Dar respuesta a las siguientes operaciones :
15.1 𝑨 ∪ 𝑩
A)
[𝟐𝟑°; 𝟐𝟏°]
B)
[𝟐𝟎°; 𝟐𝟔]
C)
〈𝟑𝟐°; +∞〉
D)
[𝟐𝟑°; 𝟑𝟐°]
E)
⟨𝟐𝟎°; 𝟑𝟓°]
15.2 𝑨 ∩ 𝑩
A)
〈𝟐𝟎°; 𝟐𝟑°〉
B)
⟨𝟑𝟐°; 𝟑𝟓°]
C)
[𝟐𝟑°; 𝟑𝟐°]
D)
[𝟑𝟐°; 𝟑𝟓°]
E)
〈𝟐𝟎°; 𝟑𝟐°〉
16. Con el problema anterior , realizar las
siguientes operaciones :
16.1 𝐴 − 𝐵
A)
⟨𝟑𝟐°; 𝟑𝟓°]
B)
〈𝟐𝟑°; 𝟑𝟐°〉
C)
[𝟐𝟎°; 𝟑𝟐°〉
D)
∅
E)
[𝟐𝟑°; 𝟑𝟓°]
16.2 𝑩 − 𝑨
A)
〈𝟐𝟑°; 𝟑𝟓°〉
B)
[𝟐𝟎°;𝟑𝟐°⟩
C)
[𝟐𝟎°; 𝟐𝟑°]
D)
[𝟐𝟎°; 𝟑𝟓°]
E)
〈𝟐𝟎°; 𝟐𝟑°〉](https://image.slidesharecdn.com/mat-221112140247-8b91aa08/85/MAT-Y-RAZ-MATEMATICO-I-2023-I-pdf-21-320.jpg)
![21
MATEMÁTICA Y RAZONAMIENTO
MATEMÁTICO I
17. En un estudio sobre la tensión arterial normal
se determina que de 20 a 24 años se
encuentran entre [79; 120] mientras que de
40 a 44 años se encuentra entre [83; 125]
¿Cuál es la diferencia entre la tensión arterial
normal del grupo de menor edad respecto al
del grupo de mayor edad?
A)
[𝟕𝟗; 𝟖𝟑⟩
B)
[𝟖𝟑; 𝟏𝟐𝟓]
C)
〈𝟖𝟑; 𝟏𝟐𝟓〉
D)
⟨𝟕𝟗; 𝟏𝟐𝟎]
E)
[𝟏𝟐𝟎; 𝟏𝟐𝟓]
18. Un grupo A de personas sale a correr durante la
mañana entre los siguientes horarios
[6: 30; 8: 15] y un grupo B sale a correr de
[6: 15; 7: 50]¿En qué intervalo de horas hay
gente más corriendo?
A)
[6: 15; 8: 15⟩
B)
⟨6: 20; 8: 00]
C)
[6: 30; 8: 15]
D)
[ 6: 30; 7: 50]
E)
⟨ 6: 30; 8: 15]
19. Se tomó temperatura al volcán Coropuna,
obteniéndose los siguientes intervalos de
temperatura en grados centígrados, durante el
mes de mayo [−12; 10] , junio [−14; 8] y
julio[−13; 9] .Durante ese trimestre ¿Cuál
fue el intervalo de temperatura en el que
coincidieron?
A)
[−10;2⟩
B)
[−12,8]
C)
〈−14;6〉
D)
[−13; 9 ⟩
E)
〈−15;10〉
20. Se conoce que la cantidad de sodio que
consume un deportista es importante, se ha
realizado una comparación entre 3 deportistas
es así que la cantidad de sodio (expresado en
intervalos) en el deportista A está entre
[136,98;145,77] en un deportista B entre
[134,21;148,12] y el deportista C entre
[133,10;144,32] . ¿Entre qué valores puede
variar la cantidad de sodio de los 3 deportistas?
A) [134,21;148,12]
B) [133,10;148,12]
C) [136,98;145,77⟩
D) [136,98;145,77]
E) ⟨134,21;144,32]](https://image.slidesharecdn.com/mat-221112140247-8b91aa08/85/MAT-Y-RAZ-MATEMATICO-I-2023-I-pdf-22-320.jpg)



![26 PRECATÓLICA 2023-I
MATEMÁTICA Y RAZONAMIENTO
MATEMÁTICO I
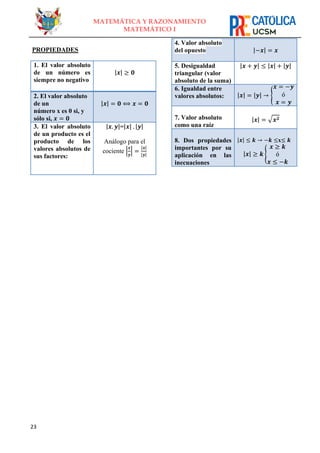
9. Resolver:
|−8|+|
3(2𝑥−5)
−9
|=|10|
A)
{−
7
2
;
11
3
}
B)
{
8
5
;
10
2
}
C)
{−
1
2
;
11
2
}
D)
{−
1
9
;
13
2
}
E)
{−
17
2
;
11
6
}
10. El producto de las raíces de la ecuación es:
2|𝑥 − 3|2
+ |7𝑥 − 21| − 15 = 0
A)
27
4
B)
20
6
C)
13
5
D)
21
4
E)
31
3
11. Resolver:
(𝑥 − 3)2
+6|𝑥 − 3| − 27 =0
A)
{0; 3}
B)
{−5;6}
C)
{−2;7}
D)
{0;6; }
E)
{3; 8}
12. Resolver:
A)
[−3;+∞⟩
B)
[−3; 1]
C)
〈−∞; 2〉
D)
〈−∞; 8]〉
E)
[−2; 4]
|𝑥2
+ 2𝑥 − 3 −| < |𝑥2
− 3𝑥 + 7|](https://image.slidesharecdn.com/mat-221112140247-8b91aa08/85/MAT-Y-RAZ-MATEMATICO-I-2023-I-pdf-27-320.jpg)
![27 PRECATÓLICA 2023-I
MATEMÁTICA Y RAZONAMIENTO
MATEMÁTICO I
13. Resolver la siguiente inecuación :
|3𝑥 − 2| < |6 − 𝑥|
A)
〈−𝟗; 𝟐〉
B)
[−𝟐; 𝟖]
C)
[ 𝟓;𝟒⟩
D)
〈−𝟐; 𝟐〉
E)
[𝟐; 𝟓]
14. Hallar la suma de las raíces enteras siguiente
inecuación :
| 3 − 𝑥| ≥ |3𝑥 − 5|
A) 4 B) 2 C) 1 C)8 E)3
15. Hallar la siguiente inecuación en :
|3 − |2𝑥 + 3|| < 2
A) ⟨−4;2] ∪ 〈−1; 1〉
B) ⟨−∞;2] ∪ ⟨4; +∞⟩
C) ⟨−2;−1] ∪ 〈−5;4〉
D) ⟨−∞;−2] ∪ ⟨−1; +∞⟩
E) ⟨−2;−1] ∪ 〈3; 4〉
16. Si se sabe que el valor absoluto de doble de la
edad de Jorge aumentada en 4 es igual a 24.
¿Cuántos años tiene Jorge?
A) 10 B)12 C) 11 D)5 E)8](https://image.slidesharecdn.com/mat-221112140247-8b91aa08/85/MAT-Y-RAZ-MATEMATICO-I-2023-I-pdf-28-320.jpg)

















![46 PRECATÓLICA 2023 - I
MATEMÁTICA Y RAZONAMIENTO
MATEMÁTICO I
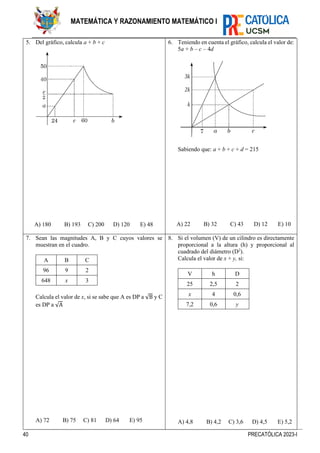
4.2. Incompatible
No tiene solución
También se le llama inconsistente
Además, se cumple que:
𝑎
𝑚
=
𝑏
𝑛
≠
𝑐
𝑝
Interpretación gráfica: corresponde a dos
rectas paralelas
Ejemplo
Gráficamente el sistema:
{
𝑥 − 𝑦 = 3 … (1)
𝑥 − 𝑦 = 5 … (2)
Sería tal como se muestra:
Dado que las rectas son paralelas y no tienen
ningún punto en común, por lo tanto, el
sistema no tiene solución.
5. Inecuaciones de primer grado con una variable
Una inecuación es una relación de orden que se da
entre dos expresiones matemáticas considerando
por lo menos una variable, se presenta de la
siguiente forma:
𝑎𝑥 + 𝑏 ≥ 0
𝑎𝑥 + 𝑏 ≤ 0
𝑎𝑥 + 𝑏 < 0
𝑎𝑥 + 𝑏 > 0
Considerando que: a; bR, a 0
6. Resolución de una inecuación de primer grado
Es hallar un conjunto de valores que satisfacen la
desigualdad, que es expresado a través de un
intervalo denominado conjunto solución.
Para la resolución de una inecuación de primer
grado se efectuarán las operaciones indicadas y
luego despejar la variable tomando en cuenta los
teoremas de las desigualdades.
Ejemplos
a) Determinar el conjunto solución de:
3𝑥 − 12 ≤ 4(𝑥 − 7)
Solución:
3𝑥 − 12 ≤ 4(𝑥 − 7)
Efectuamos la operación:
3𝑥 − 12 ≤ 4𝑥 − 28
Despejamos y reducimos:
16 ≤ 𝑥
∴ 𝑥 ∈ [16; +∞[
b) Indicar el mayor valor entero que puede tomar
x en la siguiente inecuación:
3𝑥 + (𝑥 − 3)2
> (𝑥 − 5)(𝑥 + 3)
Solución:
3𝑥 + (𝑥 − 3)2
> (𝑥 − 5)(𝑥 + 3)
Efectuamos las operaciones:
3𝑥 + 𝑥2
− 6𝑥 + 9 > 𝑥2
− 2𝑥 − 15
Reducimos:
24 > 𝑥
∴ 𝑥 ∈ ]−∞; 24[
→ 𝑥 = 23
7. SISTEMAS DE INECUACIONES CON UNA
VARIABLE
Dadas dos o más de inecuaciones de primer grado
con una incógnita estarían formando un sistema de
inecuaciones.
Para resolver un sistema de inecuaciones primero
se resuelven cada una de las inecuaciones que
forma parte del sistema y la solución del sistema es
la intersección de los diferentes conjuntos
soluciones de las inecuaciones que formaron parte
del sistema.
Ejemplos
a) Determinar el conjunto solución de:
−2(5 − 𝑥) + 8 < 3𝑥 + 5(𝑥 − 4) ≤ 15 + 𝑥
Solución
Primero se generan las dos inecuaciones
−2(5 − 𝑥) + 8 < 3𝑥 + 5(𝑥 − 4)
3𝑥 + 5(𝑥 − 4) ≤ 15 + 𝑥
Luego se resuelven de manera independiente
cada una:
−2(5 − 𝑥) + 8 < 3𝑥 + 5(𝑥 − 4)
−10 + 2𝑥 + 8 < 3𝑥 + 5𝑥 − 20
18 < 6𝑥
3 < 𝑥 CS 1
−∞ 3 + ∞
3𝑥 + 5(𝑥 − 4) ≤ 15 + 𝑥
3𝑥 + 5𝑥 − 20 ≤ 15 + 𝑥
7𝑥 ≤ 35
𝑥 ≤ 5 CS 2](https://image.slidesharecdn.com/mat-221112140247-8b91aa08/85/MAT-Y-RAZ-MATEMATICO-I-2023-I-pdf-47-320.jpg)
![47 PRECATÓLICA 2023 - I
MATEMÁTICA Y RAZONAMIENTO
MATEMÁTICO I
−∞ 5 + ∞
Luego se interceptan los conjuntos solución y
obtenemos la solución del sistema
−∞ 3 5 + ∞
C.S. ]3; 5]
b) La edad de Ricardo es un número impar. Si
a la cuarta parte de su edad se le agrega 4 resulta
menor que la tercera parte de su edad; mientras
que a la mitad de su edad se le suma 9, el
resultado es menor que 40. Calcular la edad de
Ricardo sabiendo que es la menor posible.
Solución:
Edad de Ricardo = x
Planteamos la primera inecuación:
𝑥
4
+ 4 <
𝑥
3
mcm: 12
3𝑥 + 48 < 4𝑥
48 < 𝑥
Planteamos la segunda inecuación:
𝑥
2
+ 9 < 35
𝑥
2
< 26
𝑥 < 52
𝑥 ∈ ]48; 52[
∴ La edad de Ricardo es 49 años
48 52
−∞ +∞](https://image.slidesharecdn.com/mat-221112140247-8b91aa08/85/MAT-Y-RAZ-MATEMATICO-I-2023-I-pdf-48-320.jpg)