Descargado 13 veces
Subido porCristian Fernando Guerrero Montoya
Operaciones con polinomios
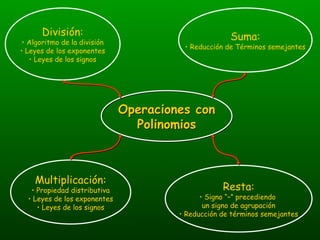
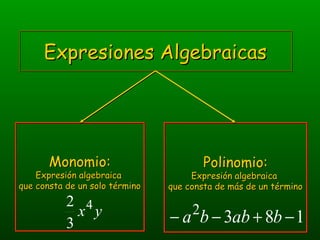
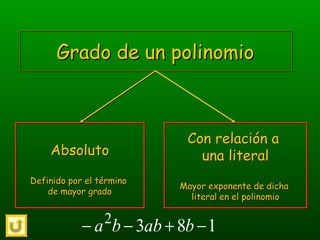
El documento habla sobre operaciones con polinomios como suma, resta, multiplicación y división. Explica que la suma y resta implican reducir términos semejantes, mientras que la multiplicación usa la propiedad distributiva y las leyes de exponentes. La división sigue el algoritmo de división numérica y también usa las leyes de exponentes.
Más contenido relacionado
Similar a Operaciones con polinomios
Más de Cristian Fernando Guerrero Montoya
Operaciones con polinomios
- 1. Operaciones con Polinomios ConsueloDíaz Raquel Valdés
- 2. Multiplicación: • Propiedad distributiva •Leyes de los exponentes • Leyes de los signos Operaciones con Polinomios Operaciones con Polinomios División: • Algoritmo de la división • Leyes de los exponentes • Leyes de los signos Suma: • Reducción de Términos semejantes Resta: • Signo “–” precediendo un signo de agrupación • Reducción de términos semejantes
- 4. Expresiones AlgebraicasExpresiones Algebraicas Monomio: Expresiónalgebraica que consta de un solo término Monomio: Expresión algebraica que consta de un solo término Polinomio: Expresión algebraica que consta de más de un término Polinomio: Expresión algebraica que consta de más de un término 1832 −+−− babbayx4 3 2
- 5. Grado de unpolinomioGrado de un polinomio Absoluto Definido por el término de mayor grado Absoluto Definido por el término de mayor grado Con relación a una literal Mayor exponente de dicha literal en el polinomio Con relación a una literal Mayor exponente de dicha literal en el polinomio 1832 −+−− babba
- 6. babba 72 2 +− Sumar con 1432 −+−− babba ( )babba 72 2 +− ( )143 2 −+−− babba( ) ( )14372 22 −+−−++− babbababba
- 7. ( ) ()=−+−−++− 14372 22 babbababba =−+−−+−= 14372 22 babbababba ¡¡ Reducción de términos semejantes !! 1852 −+−−= babba
- 8. babba 72 2 +− De restar 1432 −+−− babba ( ) ( )14372 22 −+−−−+− babbababba( )babba 72 2 +− ( )143 2 −+−− babba
- 9. =+−+++−= 14372 22 babbababba Reducciónde términos semejantes ( ) ( )=−+−−−+− 14372 22 babbababba Signos de agrupación 1635 2 +++= babba Ejercicios
- 10. Revisitando un ejemplo... 12340xxxx 432 234 +++ 1234 432 23 +++ xxx 10=x 10× x× ¿qué sucedió con las expresiones algebraicas?
- 11. xxxx 432 234 +++= () =⋅+++ xxxx 432 23 =+++= xxxxxxx 432 23 multiplicación Propiedad distributiva Leyes de los exponentes
- 12. babba 72 2 +− Multiplicar por 1−b () ( )172 2 −•+− bbabba( )babba 72 2 +− ( )1−b
- 13. Propiedad distributiva ( )()=−+− 172 2 bbabba ( )( )12 2 −bba ( )( )17 −bb( )( )1−− bab+ +
- 14. Propiedad distributiva ( )()12 2 −bba ( )( )17 −bb( )( )1−− bab+ + ( )( ) ( )( )122 22 −+ babba ( )( ) ( )( )1−−+− abbab ( ) ( )( )177 −+ bbb + + bbababbaba 7722 22222 −++−− Ejercicios
- 15. Recordando la división numérica 45 5 61 2 3 - 3 6 9 5 6 7 - 8 4 1 1 6 9 - 1 0 8 8
- 16. División de polinomios 275423 −−+ xxx2+x 2 4x ( )23 84 xx +− 27 −− x¿ cuál es el siguiente paso ? 2 3x− x3− ( )xx 63 2 −−− x− 2− Ejercicios 1− ( )2−−− x 0
Notas del editor
- #11 Hacer el ejercicio con un 13, con 105 y luego hacer una division. Concluir sobre las leyes de los exponentes.
- #12 Hacer el ejercicio con un 13, con 105 y luego hacer una division. Concluir sobre las leyes de los exponentes.
- #16 Hacer el ejercicio con un 13, con 105 y luego hacer una division. Concluir sobre las leyes de los exponentes.
- #17 Hacer el ejercicio con un 13, con 105 y luego hacer una division. Concluir sobre las leyes de los exponentes.