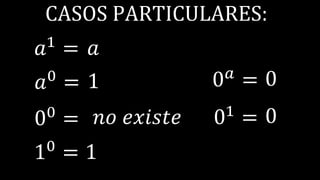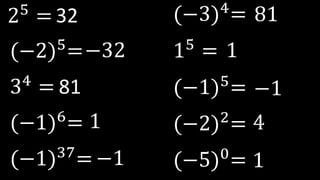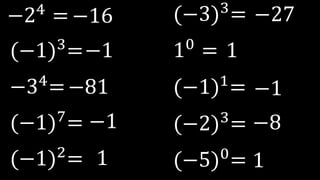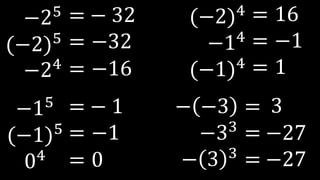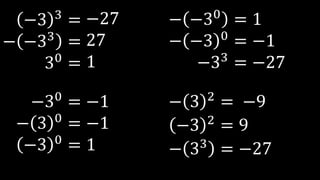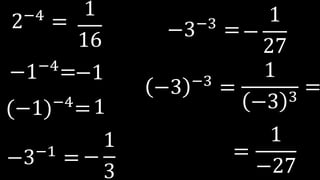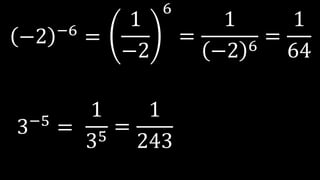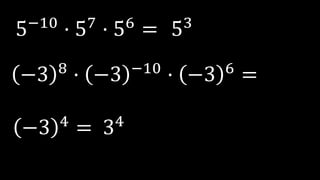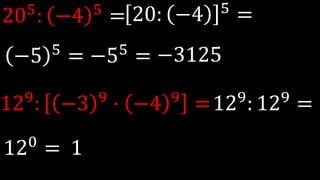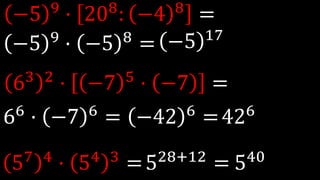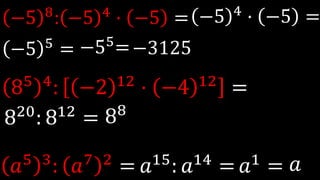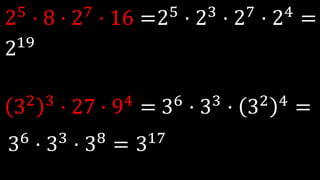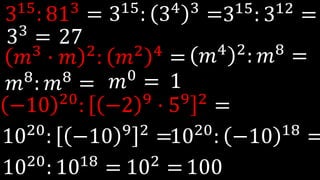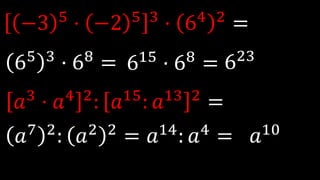Este documento explica las potencias, incluyendo definiciones, casos particulares como potencias de números negativos y ceros, y propiedades como el producto, división, y potencias de potencias. Proporciona ejemplos para ilustrar conceptos y ejercicios resueltos para practicar la reducción de expresiones de potencias.