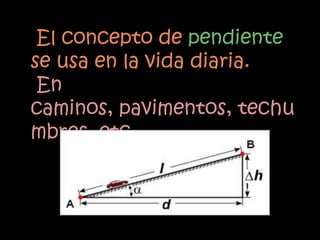
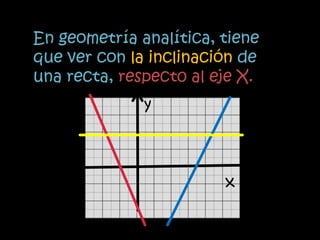
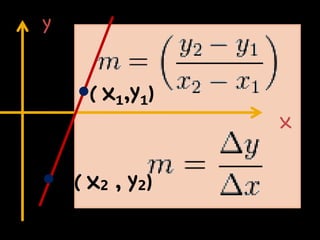
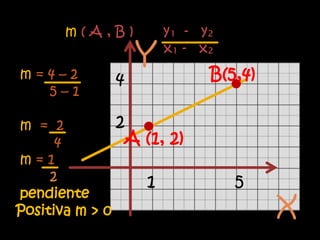
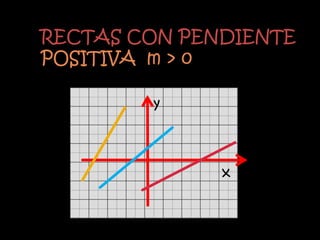
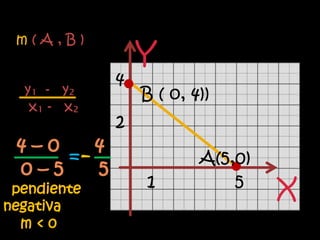
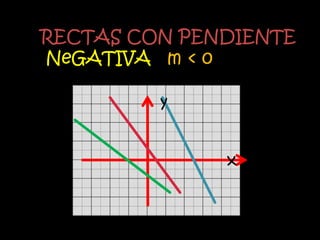
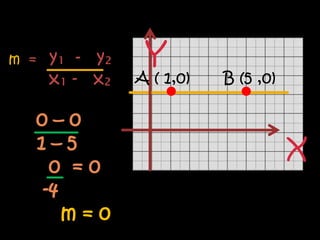
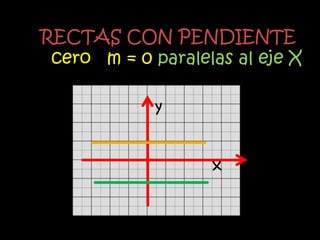
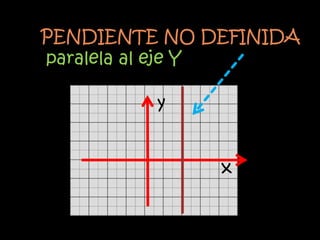
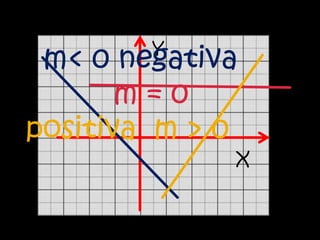
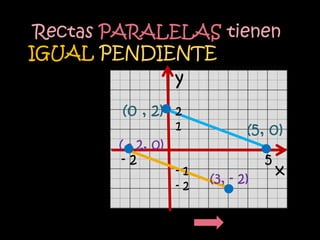
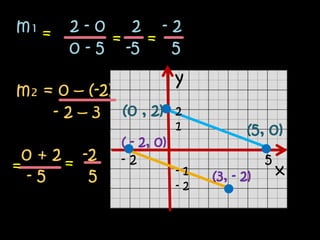
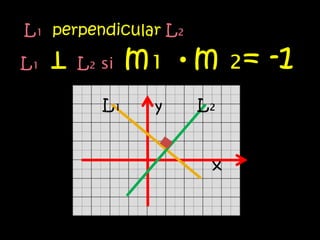
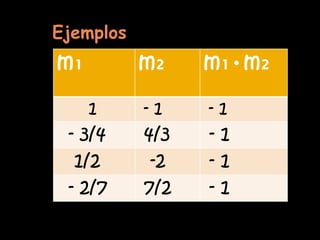
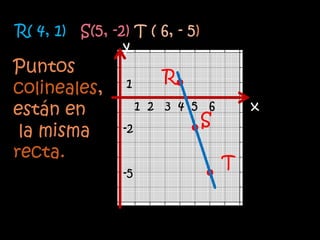
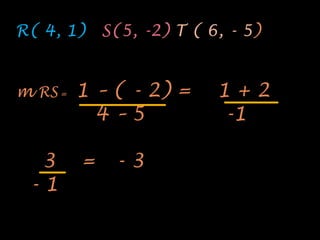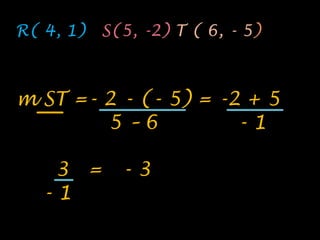El documento explica el concepto matemático de pendiente, que se refiere a la inclinación de una recta. Define la pendiente como la diferencia entre las coordenadas y de dos puntos dividida por la diferencia entre sus coordenadas x. Explica que rectas paralelas tienen la misma pendiente, mientras que rectas perpendiculares tienen pendientes cuyo producto es -1. Como ejemplo, demuestra que tres puntos dados están en la misma recta calculando que tienen la misma pendiente.

1. PENDIENTE DE
UNA RECTA
María Pizarro Aragonés

2. En matemáticas y ciencias
aplicadas se denomina
pendiente a la inclinación
de un elemento respecto
de la horizontal.

3. El concepto de pendiente
se usa en la vida diaria.
En
caminos, pavimentos, techu
mbres, etc…

4. En geometría analítica, tiene
que ver con la inclinación de
una recta, respect0 al eje X.
y
x

5. Definición
Si A ( x₁ , y₁) y B ( x₂ , y₂ ) son
puntos en el plano, se denomina
PENDIENTE ( m ) :
m (A,B) = y₁ - y₂
x₁ - x₂

6. OTRA FORMA
Delta : diferencia
En una recta, la pendiente
es siempre constante.

7. y
( x₁,y₁)
x
( x₂ , y₂)

8. Calcula la pendiente entre los
puntos R ( 3, - 1) y S ( 5 , - 4)
m= y₁ - y₂
x₁ - x₂
m = - 4 - (- 1) - 4 + 1 -3
5 - 3 = 2 = 2

9. Calcula la pendiente entre los
puntos M ( -1, 5) y T ( -2 , 5 )
m= y₁ - y₂
x₁ - x₂
m= 5 - 5 0 =
- 2 - ( - 1)
=-2+1
0 = 0
-1

10. m(A,B) y₁ - y₂
Y x₁ - x₂
m=4–2 4 B(5,4)
5–1
m = 2 2
4 A (1, 2)
m=1
2 1 5
pendiente
Positiva m > 0 X

11. RECTAS CON PENDIENTE
POSITIVA m > 0
y
x

12. m(A,B)
Y
4
y₁ - y₂ B ( o, 4))
x₁ - x₂
2
4–0 4
=- A(5,0)
0–5 5
1 5
pendiente
negativa
X
m<0

13. RECTAS CON PENDIENTE
NeGATIVA m < 0
y
x

14. m = y₁ - y₂ Y
x₁ - x₂ 4 A ( 1,0) B (5 ,0)
0–0 2
1–5 X
0 =0
-4
m=0

15. RECTAS CON PENDIENTE
cero m = 0 paralelas al eje X
y
x

16. PENDIENTE NO DEFINIDA
paralela al eje Y
y
x

17. Y
m< 0 negativa
m=0
positiva m > 0
X

18. Rectas PARALELAS tienen
IGUAL PENDIENTE
y
(0 , 2) 2
1 (5, 0)
( - 2, 0)
-2 5
-1
(3, - 2)
x
-2

19. m₁ = 2-0 2 -2
= =
0 - 5 -5 5
m₂ = 0 – (-2)
y
- 2 – 3 (0 , 2) 2
1 (5, 0)
( - 2, 0)
0 + 2 = -2 -2 5
= -1 x
-5 5 -2
(3, - 2)

20. Si m₁=m₂
las rectas son
paralelas

21. Si el producto de las pendientes
es -1 , las rectas son
perpendiculares.
m₁• m₂ = -1

22. L₁ perpendicular L₂
L₁ L₂ si m₁ •m ₂= -1
L₁ y L₂
x

23. Ejemplos
m₁ m₂ m₁•m₂
1 -1 -1
- 3/4 4/3 -1
1/2 -2 -1
- 2/7 7/2 -1

24. a . -b
b a
= -1
La fracción recíproca,
con signo contrario.

25. Aplicando el concepto de
pendiente, demostrar que los
puntos R( 4, 1)
S(5, -2) T ( 6, - 5) son
colineales. Es decir pertenecen
a la misma recta.
Se calcula la pendiente entre
R y S y entre S y T si son
iguales, los puntos son
colineales.

26. R( 4, 1) S(5, -2) T ( 6, - 5)
m RS = 1 – ( - 2) = 1+2
4–5 -1
3 = -3
-1

27. R( 4, 1) S(5, -2) T ( 6, - 5)
m ST =- 2 - (- 5) = -2 + 5
5–6 -1
3 = -3
-1

28. R( 4, 1) S(5, -2) T ( 6, - 5)
y y
Puntos
1 R
colineales,
están en 1 2 3 4 5 6 x
S
la misma -2
recta.
T
-5

29. FIN
Bibliografía : Wikipedia