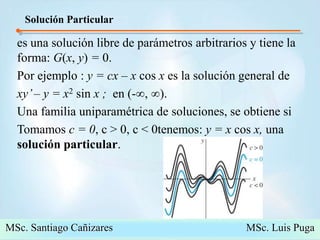
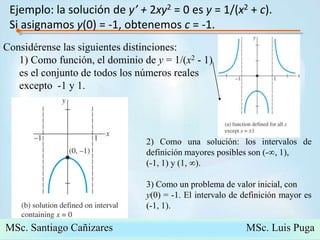
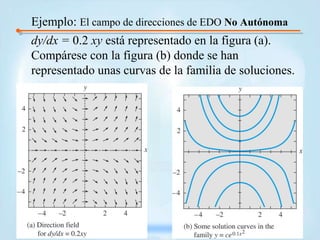
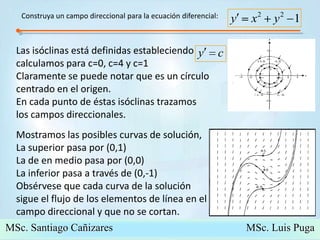
El documento introduce conceptos básicos sobre ecuaciones diferenciales. Explica que una ecuación diferencial relaciona una función desconocida con sus derivadas. Luego clasifica las ecuaciones diferenciales como ordinarias o parciales dependiendo del número de variables independientes, y define notación común como la de Leibniz.

1. 1Módulo de Ecuaciones DiferencialesMSc. Santiago Cañizares MSc. Luis PugaMSc. Santiago Cañizares MSc. Luis Puga

2. Introducción a las Ecuaciones DiferencialesUna de las más importantes y fascinaste ramas de las matemáticas que permiten modelar diversos fenómenos físicos que surgen en la naturaleza son las Ecuaciones Diferenciales, las mismas que junto con el Cálculo Integral y Diferencial dan respuestas a los mismos.MSc. Santiago Cañizares MSc. Luis Puga

3. Definiciones básicas y notaciónMSc. Santiago Cañizares MSc. Luis Puga

4. 4¿Qué es una ecuación diferencial?Función diferenciable en (-, ). Su derivada es: Ejemplo de ecuacióndiferencial Imaginemos que nos dan directamente esta ecuación. Intentaremos contestar preguntas del tipo: ¿Qué función representa y(x)? ¿Cómo se resuelve semejante ecuación?MSc. Santiago Cañizares MSc. Luis Puga

5. 5DEFINICIONES1) Es una ecuación que contiene las derivadas de una o más variables dependientes, con respecto a una o más variables independientes.variable dependientevariable independienteMSc. Santiago Cañizares MSc. Luis Puga

6. 62) Es una ecuación que involucra una función desconocida y sus derivadas.3)Es una ecuación que contiene derivadas o diferenciales de una función incógnita.MSc. Santiago Cañizares MSc. Luis Puga

7. Notación7La notación a utilizarse en la escritura de ecuaciones diferenciales es en base a las derivadas y diferenciales, pueden ser de acuerdo a:Notación de Leibniz: dy/dx, d2y/ dx2,...Notación Prima: y', y'', y'''… y(n),...Notación de Newton: Notación de subíndice: ux, uy, uxx, uyy, uxy, …MSc. Santiago Cañizares MSc. Luis Puga

8. 8En la notación de Leibniz localizamos rápidamente cuál es la variable dependiente y la independiente:MSc. Santiago Cañizares MSc. Luis Puga

9. 9ClasificaciónLas EDs se clasifican por tipo, orden y linealidad.Por el tipo:i) Ecuación diferencial ordinaria (EDO):Una ecuación que contiene sólo derivadas ordinarias de una o más variables dependientes de una sola variable independiente. Ejemplo de EDO: Una EDO puede contener más de una variable dependiente:MSc. Santiago Cañizares MSc. Luis Puga

10. 10ii) Ecuación diferencial parcial (EDP): Una ecuación que contiene derivadas parciales de una o más variables dependientes de dos o más variables independientes.Ejemplos:MSc. Santiago Cañizares MSc. Luis Puga

11. 11Clasificación según el orden:El orden de una ecuación diferencial (ya sea EDO o EDP) es el orden mayor de la derivadas involucradas en la ecuación.Ejemplo:Término Segundo orden Término Primer orden Luego, es una EDO de segundo ordenY las EDO pueden ser de primero, segundo, …, n-ésimo orden.MSc. Santiago Cañizares MSc. Luis Puga

12. 12Grado:El grado de una ecuación diferencial es el grado algebraico de su derivada de mayor orden. Es decir, el grado de una ecuación diferencial es la potencia a la que esta elevada la derivada que nos da el orden de la ecuación diferencial.Ejemplo:La siguiente ecuación diferencial:es de primer grado, dado que la segunda derivada, que nos da el orden de la EDO, está elevada a uno.MSc. Santiago Cañizares MSc. Luis Puga

13. 13Clasificación según la LinealidadSe dice que una EDO de orden n es lineal si F(en la forma general) es lineal eny, y’, y”, …, y(n).O bien:Nótese que las derivadas n-ésimas y el término en y están elevados a la potencia 1, de ahí que la ecuación es lineal.MSc. Santiago Cañizares MSc. Luis Puga

14. FORMAS DE ESCRIBIR UNA EDOForma general de orden n de una EDO:Forma normal de orden n de una EDO:MSc. Santiago Cañizares MSc. Luis Puga14MSc. Santiago Cañizares MSc. Luis Puga

15. Propedeutico Maestría 2008 DEPFIE-UMSNH José Juan Rincón PasayeFORMAS DE ESCRIBIR UNA EDOPor ejemplo de la Ecuación Diferencial:Su forma general es: y su forma normal es: MSc. Santiago Cañizares MSc. Luis Puga15MSc. Santiago Cañizares MSc. Luis Puga

16. 16También la podemos escribir en forma diferencialPor ejemplo, supongamos que y es la variable dependiente y x la independiente en la EDO en forma diferencial:MSc. Santiago Cañizares MSc. Luis Puga

17. 17Ejercicios y tallerDeterminar el grado y orden de las siguientes ecuaciones:a)b)NOTA: cuando alguna derivada esté dentro de un radical o en polinomio, que a su vez esté elevado a una potencia fraccionaria, tendremos que eliminar dicho radical para determinar el grado de la ecuación diferencial.MSc. Santiago Cañizares MSc. Luis Puga

18. 18EjerciciosDeterminar el orden y grado de las siguientes ecuaciones diferenciales:a) b)c)d)MSc. Santiago Cañizares MSc. Luis Puga

19. Ecuaciones Diferenciales Lineales de orden nMSc. Santiago Cañizares MSc. Luis Puga

20. 20Una EDO lineal de orden n, debe cumplir con dos condiciones:i) La variable dependiente y todas sus derivadas son de primer grado, es decir:y, y’, y”, …, y(n) son de primer grado.ii) Los Coeficientes a0, a1, …,andependen solo de la variable independiente x.MSc. Santiago Cañizares MSc. Luis Puga

21. Propedeutico Maestría 2008 DEPFIE-UMSNH José Juan Rincón PasayeUna EDO no lineal es simplemente una Ecuación que no es lineal.Ejemplo:El coeficiente depende de y.Función no lineal de y.21MSc. Santiago Cañizares MSc. Luis Puga

22. 22Determinar si las EDOS son ¿Lineales o no lineales?1)2)3)4)5)MSc. Santiago Cañizares MSc. Luis Puga

23. 23Forma general:Estas ecuaciones de acuerdo a g(x) y a los coeficientes pueden ser:Lineal homogénea: El término independiente g(x) es nulo.Lineal con coeficientes constantes: Los coeficientes a0(x),...,an(x) son constantes.Lineal con coeficientes variables: Enfatiza el hecho de que al menos uno de los coeficientes a0(x),...,an(x) NO es constante.MSc. Santiago Cañizares MSc. Luis Puga

24. Solución de una Ecuación Diferencial OrdinariaMSc. Santiago Cañizares MSc. Luis Puga

25. Solución de una EDOLa solución de una EDO es una función, es decir la relación existente entre la variable independiente y la variable dependiente. Sea la función Y f una función definida en el intervalo I, tal que sea derivable ( sea continua y admita n-ésimas derivadas). f es solución de la ecuación F en el intervalo I, si cumple dos condiciones:MSc. Santiago Cañizares MSc. Luis Puga

26. Propedeutico Maestría 2008 DEPFIE-UMSNH José Juan Rincón PasayeCondiciones para que f sea Solución de una EDO FLa debe estar definidaQue al sustituirse en la EDO las n derivadas y la función y, reducen la ecuación a la identidad: Si i) y ii) son verdaderas entonces f es la solución explícita de F.Siempre hemos de considerar una solución junto a su intervalo I,de definición, también llamado intervalo de existencia de validezo dominio de definición.MSc. Santiago Cañizares MSc. Luis Puga

27. 27Una EDO puede tener:Infinitas soluciones:Nótese que C puede tomar infinitos valoresUna única solución:y(x) es un valor ya establecido (0).Ninguna solución:MSc. Santiago Cañizares MSc. Luis Puga

28. 28Ejemplo: comprobación de una solución.Comprobar que la función y = x4/16 , es la solución de la EDO dy/dx = xy1/2 en el intervalo (-, ):Método 1 Solución: Existe la derivada dy/dx = x3/4para todo x de (-, ).(a) Lado izquierdo : Lado derecho: Y la igualdad se cumple para todo x de (-, ).MSc. Santiago Cañizares MSc. Luis Puga

29. Ejemplo: comprobación de una solución.Método 2 Expresamos la ecuación diferencial en su forma general:Reemplazamos en la ecuación general la y el valor de se cumple la identidad 0 = 0, para todo x de (-, )29MSc. Santiago Cañizares MSc. Luis Puga

30. 30Solución:Derivando la solución dos veces: y' = xex+ ex y'' = xex+ 2exNótese que y(x) = 0 también es solución tanto de este ejemplo como del anterior en el intervalo(-, ). A y(x) = 0se la conoce como solución trivial.MSc. Santiago Cañizares MSc. Luis Puga

31. 31Comprobar que la y = x2 + C no es solución de la ecuación diferencial:Solución:Derivando y = x2 + CtenemosSustituyendo el valor de la derivada encontrada en la ecuación diferencial tenemos: Por lo tanto y = x2 + C no es solución de la ecuación diferencial MSc. Santiago Cañizares MSc. Luis Puga

32. 32Ejercicios Determine si cada Función es solución o no de la ecuación diferencial dada:MSc. Santiago Cañizares MSc. Luis Puga

33. Propedeutico Maestría 2008 DEPFIE-UMSNH José Juan Rincón PasayeFamilia de Curvas y su Ecuación DiferencialSi se tiene una ecuación de una familia de curvas, se puede obtener la ecuación diferencial, mediante la eliminación de las constantes o parámetros y esto se obtiene aislando la constante en un miembro de la ecuación y derivando. También se puede eliminar la constante derivando la ecuación dada, tantas veces como constantes arbitrarias tenga, y se resuelve el sistema formado con la ecuación original.33MSc. Santiago Cañizares MSc. Luis Puga

34. 34Ejemplo:Encuentre la ED cuya solución general es y = x2 + C.SoluciónObservemos que sólo aparece una constante de integración, de manera que derivamos una sola vez la solución general y = x2 + C. AsíComo en esta derivada no aparecen constantes de integración, quiere decir que esta es la ED de la solución general propuesta.MSc. Santiago Cañizares MSc. Luis Puga

35. 35EjemploEncuentre la ED cuya solución general es y = C x2.SoluciónObservemos que sólo aparece una constante de integración, de manera que derivamos una sola vez la solución general y = C x2. AsíDespejamos C de la solución general y se sustituye el valor encontrado en la ED.Por lo tanto:es la ED de la solución general, puesto que ya no aparecen constantes de integración.MSc. Santiago Cañizares MSc. Luis Puga

36. Propedeutico Maestría 2008 DEPFIE-UMSNH José Juan Rincón PasayeEjemploEncuentre la ED cuya solución general es y =Asenx+BcosxSoluciónObservemos que aparecen dos constantes de integración, de manera que derivamos dos veces:Formamos un sistema entre y e y´´ y obtenemos:Por lo tanto, la ecuación buscada es:es la ED de la solución general, puesto que ya no aparecen constantes de integración.36MSc. Santiago Cañizares MSc. Luis Puga

37. 37Función vssolución ¿y=1/x es solución de xy´+y=0?La gráfica de una solución  de una EDO se llama curva solución. Como  es una función diferenciable, es continua en su intervalo de definición I. Puede, entonces, haber diferencias entre la gráfica de la función y la solución. Veamos un ejemplo:(a) y = 1/x considerada como una función, tiene dominio de definición (-, 0) U (0, ). Es discontinua y no diferenciable en x = 0. (b) y = 1/x estambién solución de xy’ + y = 0. Se entiende que es solución en algún intervalo I en el que es diferenciable y cumple la EDO. Por ejemplo, en (0, ). MSc. Santiago Cañizares MSc. Luis Puga

38. Solución explícita de una EDO: La variable dependiente está expresada solamente en términos de variables independientes y constantes.Por ejemplo, la solución de xy' + y = 0 en (0, ) es y = (x) = 1/x.Solución implícita de una EDOUna relación G(x,y) = 0 es una solución implícita de una EDO sobre un intervalo I, siempre que exista al menos una función y = (x) que satisface tanto la relación como la ED en I.38MSc. Santiago Cañizares MSc. Luis Puga

39. 39Ejemplo: Comprobación de una solución implícita.x2+ y2= 25 es una solución implícita de dy/dx = − x/y en el intervalo -5 < x < 5; puesto que al derivar de forma implícita respecto a x:dx2/dx + dy2/dx = (d/dx)(25), 2x + 2y(dy/dx) = 0; obtenemos la EDO:dy/dx = -x/y.Despejando y de la solución implícita podemos encontrar dos soluciones explícitas:

40. Familia de soluciones o solución general: Al resolver una EDO de primer orden F(x, y, y') = 0, en general, se obtiene una solución que contiene una constante arbitraria o parámetro c. Una solución así, G(x, y, c) = 0 representa en realidad a un conjunto de soluciones, llamado familia uniparamétrica de soluciones. Cuando se resuelve una ED de orden n, se busca una familia n-paramétrica de solucionesG(x, y, c1, c2, …, cn) = 0.40Observemos que el número de constantes arbitrarias en la solución general estádeterminado por el orden de la EDO.MSc. Santiago Cañizares MSc. Luis Puga

41. 41Solución Particulares una solución libre de parámetros arbitrariosy tiene la forma: G(x,y)= 0.Por ejemplo : y = cx – x cos x es la solución general de xy’ – y = x2sin x ; en (-, ).Una familia uniparamétrica de soluciones, se obtiene siTomamos c = 0, c > 0, c < 0tenemos: y = x cos x, una solución particular.MSc. Santiago Cañizares MSc. Luis Puga

42. Ejemplo: Sin explicitarlo, hemos visto que las variables independientes y dependientes pueden usar símbolos distintos a x e y. Por ejemplo: x = c1cos(4t) x = c2 sen(4t) con c1 y c2 constantes o parámetros arbitrarios, son ambas soluciones de la EDO: x + 16x = 0.Podemos comprobar fácilmente que la suma x = c1cos 4t + c2 sin 4t es también una solución.taller42MSc. Santiago Cañizares MSc. Luis Puga

43. Problemas con valores inicialesPVI y ContornoMSc. Santiago Cañizares MSc. Luis Puga

44. Problemas de valores iniciales (PVI) Sea la solución general de la Ecuación Diferencial F(x,y,y´,…,yn)=0 el PVI, consiste en encontrar el valor de la constante C, para un y(x0) = y0, de manera que con éste se pueda determinar una solución particular de la ED.Ejemplo: en un intervalo I que contiene a xo , el problema deResolver : con condiciones: Se le llama problema de valor inicial.Y a las condiciones se las llama: condiciones iniciales.44MSc. Santiago Cañizares MSc. Luis Puga

45. 45PVIs de primer y segundo orden:Resolver:sujeta a:Resolver:sujeta a:son problemas de valor inicial de primer y segundo orden, respectivamente. Fácilmente interpretables de manera geométrica, como vemos en las figuras.MSc. Santiago Cañizares MSc. Luis Puga

46. Ejemplo: Sabemos que y = cex es una familia uniparamétrica de soluciones de la EDO: y’ = y en (-, ). Si y(0) = 3, entonces 3 = ce0 = c. Así y = 3ex es una solución de este problema de valor inicial.Si queremos una solución que pase por (1, -2), entonces la condición es: y(1) = -2. De modo que -2 = ce, c = -2e-1. Y tenemos y = -(2/e)ex.46y = 3exy = -(2/e)exMSc. Santiago Cañizares MSc. Luis Puga

47. 47Ejemplo: x = c1cos(4t) + c2sen(4t) es una solución de x + 16x = 0.Hallar una solución del siguiente PVI:x + 16x = 0, x( /2) = −2, x( /2) = 1.Solución: Sustituimos: x( /2) = − 2 en x = c1cos(4t) + c2sen(4t), y obtenemos c1 = −2. De la misma manera, a partir de x( / 2) = 1obtenemos c2= ¼. La solución pedida es: x = −2cos 4t +¼sen4t tallerMSc. Santiago Cañizares MSc. Luis Puga

48. 48Ejemplo: la solución de y’ + 2xy2 = 0 es y = 1/(x2 + c). Si asignamosy(0) = -1, obtenemos c = -1. Considérense las siguientes distinciones:1) Como función, el dominio de y = 1/(x2 - 1) es el conjunto de todos los números reales excepto -1 y 1.2) Como una solución: los intervalos de definición mayores posibles son (-, 1), (-1, 1) y (1, ).3) Como un problema de valor inicial, cony(0) = -1. El intervalo de definición mayor es (-1, 1).MSc. Santiago Cañizares MSc. Luis Puga

49. Teorema de existencia de una solución única49Sea R la región rectangular en el plano xy definida por a  x  b, c  y  d que contiene el punto (xo, yo) en su interior. Si f(x, y) y f/y son continuas en R, entonces existe algún intervalo Io: xo- h < x < xo + h, h > 0, contenido en a x  b y una función única y(x) definida en Io que es una solución del PVI .Las condiciones del teorema son suficientes, pero no necesarias...MSc. Santiago Cañizares MSc. Luis Puga

50. Propedeutico Maestría 2008 DEPFIE-UMSNH José Juan Rincón PasayeED Lineales de 1er ordenLas ED de la formaSe denominan ED Lineales, ya que su solución cumple con el Principio de Superposición respecto al término independiente q(x).Métodos para resolver una ED de Primer Orden:Análisis Caulitativo (gráfico)Técnicas AnalíticasAproximaciones Numéricas. (no se estudiará en este curso)MSc. Santiago Cañizares MSc. Luis Puga

51. Análisis CualitativoIsóclinasPara este análisis consideraremos EDOsAutónomas y NO AutónomasMSc. Santiago Cañizares MSc. Luis Puga

52. Una ecuación diferencial ordinaria de primer orden autónoma tiene la forma de es decir si la derivada es función solamente de la variable dependiente. Una ecuación diferencial ordinaria de primer orden NOautónomatiene la forma de Es decir si su derivada es una función tanto de la variable dependiente como de la independiente. MSc. Santiago Cañizares MSc. Luis Puga

53. 53Curvas solución "sin una función solución"Empezaremos nuestro estudio de EDOs de primer orden analizando una EDO cualitativamente.dy/dx = 0.2 xy = f(x, y)(a) Pendientes: Debido a que la solución y(x) de dy/dx = f(x,y) es necesariamente una función diferenciable en I, también es continua. Así, la derivada dy/dx= f(x,y) proporciona las pendientes de las rectas tangentes a las curvas solución en los puntos (x,y).(b) Elementos lineales: Suponemos que dy/dx = f(x, y(x)). El valor f(x, y) representa la pendiente de una recta, o un segmento de recta que llamaremos elemento lineal.MSc. Santiago Cañizares MSc. Luis Puga

54. 54Campo de direcciones Si para la EDO dy/dx = f(x, y) se evalúa f en una red o malla de puntos rectangular en el plano xy, y se dibuja un elemento lineal en cada nodo (x, y) de la malla con pendiente f(x, y), obtenemos el campo de direcciones o campo de pendientes.MSc. Santiago Cañizares MSc. Luis Puga

55. 55Ejemplo: El campo de direcciones de EDO No Autónomady/dx = 0.2 xyestá representado en la figura (a). Compárese con la figura (b) donde se han representado unas curvas de la familia de soluciones.

56. 56Ejemplo: Use un campo de direcciones para dibujar una curva solución aproximada de la ecuación autónomady/dx = seny, con y(0) = −3/2. Solución:Apelando a la continuidad de f(x, y) = sen y y f/y = cos y, el teorema de existencia y unicidad garantiza la existencia de una única curva solución que pasa por algún punto especificado en el plano. Ahora dividimos la región que contiene a (-3/2, 0) en una malla rectangular. Calculamos el elemento lineal de cada nodo para obtener la siguiente figura:MSc. Santiago Cañizares MSc. Luis Puga

57. 57EDO autónomas y campos de direccionesLa figura muestra el campo de direcciones de dy/dx = 2y – 2.Podemos observar que los elementos lineales que pasan por los puntos de cualquier recta horizontal mantienen la pendiente. Recordemos que una EDO autónoma es de la forma dy/dx = f(y), y las pendientes sólo dependen de y.MSc. Santiago Cañizares MSc. Luis Puga

58. Método de las IsoclinasEl procedimiento para dibujar el campo direccional puede ser simplificado construyendo primero las isóclinas.Una Isóclina es una curva en el plano xy sobre la cual la derivada de las soluciones de la ED es constante. Es decir:podemos encontrar las curvas f(x,y)= c, en donde las soluciones pasan con un mismo ángulo de inclinación. MSc. Santiago Cañizares MSc. Luis Puga

59. Procedimiento para realizar el análisis cualitativo de una EDO Construimos las isóclinas, éstas son curvas de la forma:Donde c es una constante para varios valores de C.ii) Dibujar el campo de direcciones o de pendientes. Sobre la isóclina correspondiente a la constante C, la derivada de la solución de la ecuación diferencial tiene pendiente c. Dibujar rectas tangentes con pendiente ciii) Construir soluciones.iV) Recordar que las soluciones no se intersecan.MSc. Santiago Cañizares MSc. Luis Puga

60. Construya un campo direccional para la ecuación diferencial: Las isóclinas está definidas estableciendo calculamos para c=0, c=4 y c=1Claramente se puede notar que es un círculo centrado en el origen.En cada punto de éstas isóclinas trazamos los campos direccionales.Mostramos las posibles curvas de solución,La superior pasa por (0,1)La de en medio pasa por (0,0)La inferior pasa a través de (0,-1)Obsérvese que cada curva de la solución sigue el flujo de los elementos de línea en el campo direccional y que no se cortan.MSc. Santiago Cañizares MSc. Luis Puga

61. Método de las Isoclinasa) Encontrar la ecuación de las isóclinas para la ecuación diferencial:b) ¿Qué tipo de curvas son estas isóclinas?c) Dibujar las isóclinas y con ayuda de éstas dibujar el campo de direcciones y algunas curvas solución.MSc. Santiago Cañizares MSc. Luis Puga

62. Técnicas AnalíticasMSc. Santiago Cañizares MSc. Luis Puga

63. Métodos de Solución Analítica NO existe un método general para resolver Ecuaciones Diferenciales, es decir, dada una ecuación diferencial no tenemos un procedimiento general para hallar su solución analítica.

64. Sin embargo, en algunos casos particulares bien identificados sí se tienen procedimientos para calcular dicha solución.MSc. Santiago Cañizares MSc. Luis Puga

65. Métodos de Solución Analítica El único método entonces consiste en saber Identificar el tipo de Ecuación Diferencialque se quiere resolver.

66. Si es un caso conocido. Aplicar el procedimiento correspondiente.

67. Si no es un caso conocido, intentar algún cambio de variable que la transforme en un caso conocido.MSc. Santiago Cañizares MSc. Luis Puga

68. Métodos de Solución Analítica Si no funciona lo anterior, algunas alternativas consisten en buscar soluciones:

69. Basadas en Series

70. Numéricas

71. GeométricasMSc. Santiago Cañizares MSc. Luis Puga

72. 66MSc. Santiago Cañizares MSc. Luis Puga

73. 67ECUACIONES DE PRIMER ORDEN Y DE PRIMER GRADOSe las representa de la siguiente forma:Si despejamos la derivada tenemos:Si a ésta ecuación la podemos expresar en forma:Se denomina Ecuación Diferencial Ordinaria de Variable Separable y la solución general se obtiene por integración directa.MSc. Santiago Cañizares MSc. Luis Puga