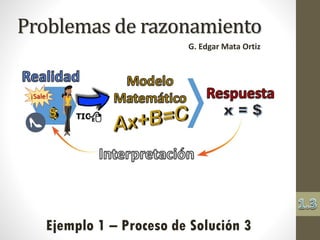
El documento presenta problemas de razonamiento donde se resuelven situaciones utilizando incógnitas, específicamente en el contexto de gastos relacionados con compras. A través de un ejemplo, se detalla el proceso de solución al determinar los precios de un vestido, zapatos y una bolsa, mostrando como distintas incógnitas pueden llevar al mismo resultado final. Se enfatiza el procedimiento algebraico necesario para plantear y resolver las ecuaciones basadas en cantidades desconocidas.

1. Problemas de razonamiento
G. Edgar Mata Ortiz

2. Problemas que se resuelven
mediante la suma de
cantidades desconocidas
Ejemplo 1.3. Proceso de solución tomando como incógnita la
última de las cantidades desconocidas para observar cómo
cambia el procedimiento pero no la solución.

3. Problemas de razonamiento
• En este ejemplo vamos a resolver el mismo
problema, pero ahora tomaremos como
incógnita la única cantidad desconocida que no
hemos empleado como equis.
• El resultado debe ser el mismo.
• El proceso algebraico va a cambiar un poco y el
valor de la equis será distinto porque representa
otra cantidad desconocida.

4. Ejemplo
• Lizbeth Eduviges compró un vestido, unos
zapatos y una bolsa de mano para su
graduación gastando un total de $3800. Si
la bolsa costó el doble que los zapatos y el
vestido costó $550 más que la bolsa,
¿cuánto costó cada artículo?

5. Procedimiento de solución
• En primer lugar debemos reconocer las
cantidades desconocidas involucradas en
el problema.
• ¿Puedes ver cuáles son?
• Menciónalas
• Asegúrate de expresar bien las cantidades
desconocidas: Expresiones como
“cantidad de”

6. Procedimiento de solución
• Las cantidades desconocidas son tres:
• Precio de los zapatos
• Precio de la bolsa
• Precio del vestido
• Vamos a identificar cualquiera de ellas con
una incógnita (“x”).
• En el ejemplo 1.1 se tomó como cantidad
desconocida el precio de los zapatos, en el
1.2, la bolsa, ahora (ejemplo 1.3)
tomaremos:
• Precio del vestido = x

7. Procedimiento de solución
• En seguida buscamos otra cantidad
desconocida que esté relacionada
directamente con el precio del vestido, en
este caso:
• “el vestido costó $550 más que la bolsa”
• Por lo tanto la bolsa cuesta $550 menos
que el vestido
• Precio de la bolsa = x – 550

8. Procedimiento de solución
• La última cantidad desconocida en este
planteamiento del problema es el precio de
los zapatos.
• El problema dice “la bolsa costó el doble que
los zapatos ”
• Entonces los zapatos costaron la mitad que la
bolsa
• Precio de los zapatos =
𝟏
𝟐
(𝒙 − 𝟓𝟓𝟎)

9. Procedimiento de solución
• Uno de los pasos más difíciles es el
planteamiento de la ecuación.
• Para este paso, es buena idea observar
cuál dato no ha sido empleado.
• En este caso, el gasto total realizado por
Lizbeth Eduviges.
• Gasto total = $3800

10. Procedimiento de solución
• La suma de los costos de cada artículo
debe ser igual a $3800
• $Zapatos + $Bolsa + $Vestido = $3800
•
𝟏
𝟐
(x – 550) + x - 550 + x = $3800

11. Procedimiento de solución
• Una vez planteada la ecuación, se
resuelve.
•
𝟏
𝟐
(x – 550) + x - 550 + x = 3800
• Se efectúan operaciones:
•
𝟏
𝟐
x – 275 + x - 550 + x = 3800
•
5
2
x – 825 = 3800

12. Procedimiento de solución
• Los términos que no tiene equis se pasan
al lado derecho de la ecuación:
•
5
2
x = 3800 + 825
• Se efectúan operaciones y se despeja “x”:
• 5x = (4625)2
• 5x = 9250
• x =
9250
5
por lo tanto
x = 1850

13. Procedimiento de solución
• Responder la pregunta:
• El precio del vestido es x = 1850
• El precio de la bolsa es x – 550 = 1300
• El precio de los zapatos es
•
1
2
(x – 550) = 650
• Total = 3800

14. GRACIAS POR SU ATENCIÓN
A pesar de haber tomado como incógnita una cantidad
desconocida distinta al ejemplo 1.1, el resultado del
problema es el mismo. No el valor de la equis, sino la
solución del problema
licmata@hotmail.com
http://licmata-math.blogspot.com
http://www.slideshare.net/licmata/
http://www.spundge.com/@licmata
https://www.facebook.com/licemata
http://www.scoop.it/t/mathematics-learning
https://sites.google.com/site/licmataalgebra/
Twitter: @licemata