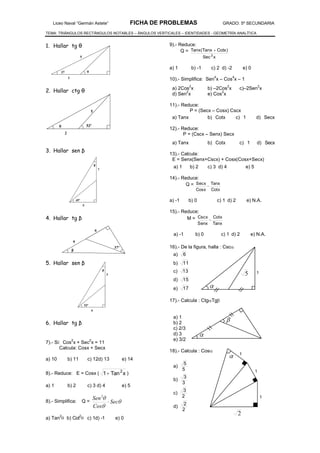
Este documento contiene 30 problemas de geometría analítica y trigonometría relacionados con triángulos rectángulos notables, ángulos verticales e identidades trigonométricas. Los problemas incluyen hallar valores trigonométricos dados ángulos, simplificar expresiones trigonométricas, calcular distancias y ángulos dados información geométrica, y resolver problemas analíticos utilizando coordenadas de puntos.

1. FICHA DE PROBLEMAS
Liceo Naval “Germán Astete”
GRADO: 5º SECUNDARIA
TEMA: TRIÁNGULOS RECTÁNGULOS NOTABLES – ÁNGULOS VERTICALES – IDENTIDADES - GEOMETRÍA ANALÍTICA
1. Hallar tg θ
9).- Reduce:
Q = Tanx(Tanx
5
2
Cotx )
Sec x
a) 1
θ
37
b) -1
c) 2 d) -2
4
e) 0
4
10).- Simplifica: Sen x – Cos x – 1
1
2
2
c)–2Sen x
11).- Reduce:
P = (Secx – Cosx) Cscx
a) Tanx
b) Cotx
c) 1
5
θ
2
b) –2Cos x
2
e) Cos x
a) 2Cos x
2
d) Sen x
2. Hallar ctg θ
53º
d) Secx
12).- Reduce:
P = (Cscx – Senx) Secx
2
a) Tanx
3. Hallar sen β
b) Cotx
c) 1
d) Secx
13).- Calcula:
E = Senx(Senx+Cscx) + Cosx(Cosx+Secx)
β
a) 1
7
b) 2
c) 3 d) 4
e) 5
14).- Reduce:
Q = Secx Tanx
Cosx
a) -1
45º
b) 0
Cotx
c) 1 d) 2
e) N.A.
5
15).- Reduce:
M = Cscx
4. Hallar tg β
Senx
6
a) -1
Cotx
Tanx
b) 0
c) 1 d) 2
e) N.A.
9
16).- De la figura, halla : Csc
37º
β
a)
b)
15
e)
3
13
d)
β
11
c)
5. Hallar sen β
6
17
5
1
17).- Calcula : Ctg Tg
53º
4
a) 1
b) 2
c) 2/3
d) 3
e) 3/2
6. Hallar tg β
2
2
7).- Si: Cos x + Sec x = 11
Calcula: Cosx + Secx
a) 10
b) 11
18).- Calcula : Cos
c) 12d) 13
a)
8).- Reduce: E = Cosx ( 1 Tan 2 x )
a) 1
b) 2
c) 3 d) 4
Sen 2
8).- Simplifica: Q =
Cos
a) Tan
2
2
b) Cot
c) 1d) -1
1
e) 14
e) 5
e) 0
1
3
b)
3
c)
Sec
5
5
3
2
2
d)
2
1
2

2. 26).- Calcula x en:
19).- Calcula : Ctg
A (2; 9)
a) 1
x
2
b)
C(9; 6)
c) 3
d) 2
e)
B (-11; 4)
5
20).- Un observador se encuentra a 24m de la
base de un poste de 7m de altura. ¿Cuál es el
ángulo de elevación respectivo?
a) 16° b) 12°
c) 14°
d) 22°
a) 3
c) 3 2 d) 5 2
b) 5
e) 7
27).- Calcula x en:
B (7; 16)
e) N.A.
13
21).- Una escalera de 6m de longitud es
apoyada sobre una pared, formando con éste
un ángulo de 30°, calcula la distancia entre los
pies de la escalera y la pared.
A (x; 4)
a) 2
a) 6
b) 4
c) 3
d) 8
22)- Desde lo alto de un edificio de 100m de
altura se observa un auto estacionado bajo un
ángulo de depresión de 60°. Calcula la
distancia desde el auto hasta el pie del edificio
en el punto que está bajo el observador.
100 3
a)
3
b)
3
3
100 3
c) 3 3 d)
5
b) 32 c) 24m d) 38m e) N.A.
24).- Desde la parte superior de un morro de
77m de altura se observa un objeto que está
ubicado a 264m del pie del morro. ¿Cuál es el
ángulo de depresión?
a) 14°
b) 16°
c) 12
d) 15
E) 9
c) 12° d) 10°
28).- Dados los puntos:
A(2; 5) , B(7; 9) y C(-3; 4)
Halla:
P
e) N.A
23).- La parte superior de un edificio de 48m de
altura es observada bajo un ángulo de
elevación de 53°. ¿Cuál es la distancia entre el
observador y el pie del edificio?
a) 36m
b) 5
e) N.A.
a) 2
3
AC 26
b) 3
AB 41 8
c) 4
d) 5
BC
5
e) 9
29).- Si dos vértices de un triángulo son A(-4; 6)
y B(-3; 8). Halla la suma de las coordenadas
del tercer vértice sabiendo que las medianas
de dicho triángulo se intersecan en el punto
P(2; 6).
a) 12 b) 13
c) 14
d) 17
e) 19
30).- De la figura, halla “a” si AB//MN.
B(1; 8)
e) N.A.
25).- La distancia entre los puntos (2; 1) y (5; 4)
M(4; 6)
es K 6 . Calcula “k”.
a)
10
b) 2 10 c) 3 10
d)
3
A
(-2; a)
a) 2
C(7; 4)
N(5/2; 3)
b) 3
c) 4
d) 5
e) 9