Este documento presenta un resumen de diferentes métodos numéricos para encontrar raíces de ecuaciones, incluyendo el método de la bisección, la interpolación lineal, el método de la secante, y el método de Newton-Raphson. Explica cada método con ejemplos numéricos y discute sus ventajas y desventajas. El objetivo es reforzar habilidades en métodos numéricos y mostrar ejercicios resueltos de análisis numérico utilizando estos enfoques.

1. Programacion Numerica
Integrante: Yhonny Ochoa
CI: 18085535
Profesor: Pedro Beltran

2. Introducción
La presente investigación emano como actividad de la materia programación numérica esta plantea para reafirmar,
estas habilidades y mostrar ejercicios con soluciones de problemas de análisis numérico primordialmente con los
siguientes métodos bisección, Interpolación lineal. Secante, Newton – Raspón y Punto fijo.
Ya sea a través del uso de computadores, creemos que es esencial una base solida en los métodos
numéricos para el futuro Ingeniero.
Por consiguiente hemos elaborado esta presentación de manera que pueda enseñarse en los extremos inferior o superior
del carrera de Ingeniería. Un aspecto de esta presentación se hace notar en la organización y alcance, que esta dividido
en 4 temas cada tema cuenta con materia introductorio y ejemplos.
Finalmente, nos hemos esforzado conscientemente en hacer esta presentación tan sencilla al usuario
como sea posible, por lo que nos empeñamos en mantener nuestras explicaciones con una orientación directa y practica.

3. Básicamente, el método consiste en dividir a la
mitad repetidamente los subintervalos de
y en cada paso, localizar la mitad que contiene a
la solución,
Esta técnica se basa en el teorema del valor intermedio y parte del supuesto
que y tienen signos opuestos. Aunque el procedimiento funciona bien
Método Bisección
para el caso en el que existe más de una solución en el intervalo
, se considera por simplicidad que es única la raíz en dicho intervalo.

4. Método Bisección
Para empezar, hacemos y calculamos el punto
medio del intervalo y lo llamamos
Observación: como en cada iteración el intervalo es la mitad del intervalo anterior, podemos concluir que en la iteración
Error Absoluto

5. Método Bisección
El método de la bisección, aunque es conceptualmente claro, tiene inconvenientes
importantes.
Es muy lento en su convergencia (es decir, tiene que ser muy grande para que sea
pequeño, por ejemplo, se requiere de 10 iteraciones para obtener un error absoluto menor
a en el ejemplo anterior), además una buena aproximación intermedia puede ser
descartada inadvertidamente.
Sin embargo, el método tiene la importante propiedad de que siempre converge a una solución,
además de que lo único que se requiere es que sea continua, es por estas razones que se
usa con frecuencia como punto de partida de métodos más eficientes.

6. Método Bisección
Para hallar el numero máximo de Iteraciones, se puede aplicar
la siguiente ecuación:
Entrada
Una “f” continua
y un intervalo de
trabajo: *[a,b]
Numero máximo
de Iteraciones (I)
Proceso
Error de
Tolerancia (E)

7. Método Bisección
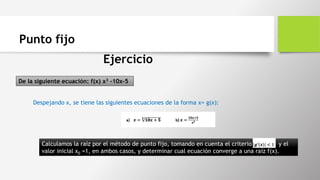
1)Aplique Bisección para encontrar soluciones, con un error de 0.01, siendo
f(x)= x3-7x2+14x-6, en b.-[1,3.2]. d.-[5,10]. Datos: a =1; b =3.2; =0.01.
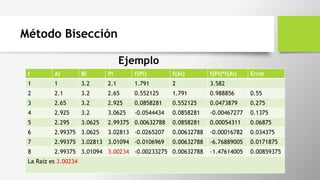
Ejemplo
Solución: El número de iteraciones se calcula con: Para este ej. I =7.78, que
debe redondearse a 8 iteraciones
I Ai Bi Pi f(Pi) f(Ai) f(Pi)*f(Ai) Error
1 1 3.2 2.1 1.791 2 3.582

8. Método Bisección
Ejemplo
I Ai Bi Pi f(Pi) f(Ai) f(Pi)*f(Ai) Error
1 1 3.2 2.1 1.791 2 3.582
2 2.1 3.2 2.65 0.552125 1.791 0.988856 0.55
3 2.65 3.2 2.925 0.0858281 0.552125 0.0473879 0.275
4 2.925 3.2 3.0625 -0.0544434 0.0858281 -0.00467277 0.1375
5 2.295 3.0625 2.99375 0.00632788 0.0858281 0.00054311 0.06875
6 2.99375 3.0625 3.02813 -0.0265207 0.00632788 -0.00016782 0.034375
7 2.99375 3.02813 3.01094 -0.0106969 0.00632788 -6.76889005 0.0171875
8 2.99375 3.01094 3.00234 -0.00233275 0.00632788 -1.47614005 0.00859375
La Raiz es 3.00234

9. Interpolación lineal y Secante
La interpolación lineal es un
procedimiento muy utilizado para
estimar los valores que toma una
función en un intervalo del cual
conocemos sus valores en los
extremos (x1, f(x1)) y (x2,f(x2)).
Para estimar este valor
utilizamos la aproximación a
la función f(x) por medio de
una recta r(x) (de ahí el
nombre de interpolación
lineal, ya que también existe
la interpolación cuadrática).
La expresión de la interpolación lineal se obtiene del
polinomio interpolador de Newton de grado uno:

10. Interpolación lineal y Secante
Para estimar un valor intermedio de una función se
aproxima la función f(x) por medio de una recta r(x), lo
que significa que la función varia linealmente con «x»
para un tramo «x = a» y «x = b»; es decir, para un valor
«x» en el intervalo (x0, x1) y (y0, y1), el valor de «y» es
dado por la línea entre los puntos y se expresa por la
siguiente relación:
(y – y0) ÷ (x – x0) = (y1 – y0) ÷ (x1 – x0)
Método

11. Para que una interpolación sea lineal, es
necesario que el polinomio de interpolación
sea de grado uno (n = 1), para que se ajuste a
los valores de x0 y x1.
La interpolación lineal está basada en
semejanza de triángulos, de tal manera
que, derivando geométricamente de la
expresión anterior, se puede obtener el
valor de «y», que representa el valor
desconocido para «x».
Interpolación lineal y Secante

12. Interpolación lineal y Secante
Así, se obtiene la ecuación general para interpolación lineal:
y = y0 + (y1 – y0) * [(x – x0) ÷ (x1 – x0)]
De esa forma se tiene que:
a = tan Ɵ = (cateto opuesto1 ÷ cateto adyacente1) =
(cateto opuesto2 ÷ cateto adyacente2)
Expresado de otra forma, es:
(y – y0) ÷ (x – x0) = (y1 – y0) ÷ (x1 – x0)
Despejando «y» de las expresiones, se tiene:
(y – y0) * (x1 – x0) = (x – x0) * (y1 – y0)
(y – y0) = (y1 – y0) * [(x – x0) ÷ (x1 – x0)]

13. En general la interpolación lineal da un error pequeño
sobre el valor real de la función verdadera, aunque el
error es mínimo en comparación a si se elige de forma
intuitiva un número próximo al que se quiere hallar.
Este error ocurre cuando se intenta aproximar el valor
de una curva con una línea recta; para esos casos se
debe disminuir el tamaño del intervalo para hacer más
precisa la aproximación.
Para mejores resultados respecto a la aproximación es
recomendable utilizar funciones de grado 2, 3 o incluso
de grados mayores para realizar la interpolación. Para
estos casos el teorema de Taylor es un herramienta
muy útil.
Interpolación lineal y Secante

14. Interpolación lineal y Secante
Veamos los pasos que tenemos que seguir para hallar la
recta de regresión:
1º. Dados los puntos de la función (x1, y1) y (x2, y2),
queremos estimar el valor de la función en un punto x en
el intervalo x1<x<x2.
2º. Para hallar la recta de interpolación nos fijaremos en
la siguiente imagen.
RECTA DE INTERPOLACIÓN LINEAL

15. Interpolación lineal y Secante
Ejemplo
•
El número de bacterias por unidad de volumen existentes en una incubación después de x horas es presentado
en la siguiente tabla. Se desea saber cuál es el volumen de bacterias para el tiempo de 3,5 horas.
Horas (x) 0 1 2 3 3.5 4
Volumen de bacterias
(y)
30 48 67 91 135

16. Interpolación lineal y Secante
Solución
•
La tabla de referencia no establece un valor que indique la cantidad de
bacterias para un tiempo de 3,5 horas pero sí se tienen valores superiores e
inferiores correspondientes a un tiempo de 3 y 4 horas, respectivamente.
De esa forma:
Ahora, se aplica la ecuación matemática para encontrar el valor
interpolado, que es la siguiente:
x0 = 3 y0 = 91
x = 3,5 y =?
x1 = 4 y1 = 135

17. Interpolación lineal y Secante
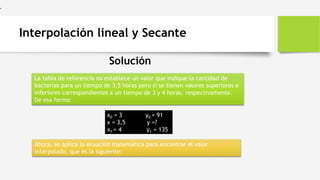
Solución
•
y = y0 + (y1 – y0) * [(x – x0) ÷ (x1 – x0)].
Luego se sustituyen los valores correspondientes:
y = 91 + (135 – 91) * [(3,5 – 3) ÷ (4 – 3)]
y = 91 + (44)* [(0,5) ÷ (1)]
y = 91 + 44 * 0,5
y = 113.
Así se obtiene que para un tiempo de 3,5
horas, la cantidad de bacterias es 113, que
representa un nivel intermedio entre el
volumen de bacterias existentes en los
tiempos de 3 y 4 horas.

18. Newton – Raspón
•
Definición
Este método es uno
de los mas utilizados
para localizar raíces
ya que en general es
muy eficiente y
siempre converge
para una función
polinomial.
Se requiere que las
funciones sean
diferenciables, y por
tanto, continuas,
para poder aplicar
este método.
Se debe partir de un
valor inicial para la
raíz: xi , este puede
ser cualquier valor,
el método convergirá
a la raíz mas
cercana.

19. Newton – Raspón
•
Si se extiende una tangente desde el punto , el punto
donde esta tangente cruza al eje x representa una
aproximación mejorada de la raíz

20. Newton – Raspón
•
La fórmula de Newton-Raphson se
deduce a partir de la fórmula de la
pendiente de una recta.
Pendiente de una recta:

21. Newton – Raspón
•
Se define la derivada de un función en un
punto dado como la pendiente a la recta
tangente de dicho punto, por lo tanto:
m=f´(x)
El valor absoluto de la diferencia de la debe
ser menor que la tolerancia o el resultado de alguna
fórmula de error debe ser menor que la tolerancia
dada.
Una de las fórmulas de error mas útiles es la del error relativo
porcentual aproximado:
100 %
Hay que determinar un numero máximo de iteraciones
Normalmente esto se hace considerando una “tolerancia” , esto es:

22. Newton – Raspón
El método de Newton-
Raphson es convergente
cuadráticamente, es decir,
el error es
aproximadamente al
cuadrado del error
anterior.
Esto significa que el numero
de cifras decimales correctas
se duplica aproximadamente
en cada interacción.

23. Newton – Raspón
Cuando el método de Newton-Raphson converge, se obtienen resultados en
relativamente pocas interacciones, ya que para raíces no repetidas este
método converge con orden 2 y el error Ei+1 es proporcional al cuadrado del
resultado anterior Ei
Supóngase que el error en una iteración es 10-n el error en la siguiente, (que es
proporcional al cuadrado del error anterior) es entonces aproximadamente 10-
2n, el que sigue será aproximadamente 10-4n etc.
De esto puede afirmarse que de cada iteración duplica
aproximadamente el numero de dígitos correctos.
Sin embargo el método de Newton-Raphson algunas veces no
converge, sino que oscila. Esto ocurre si no hay raíz real, si la raíz es
un punto de inflexión o si el valor inicial esta muy alejado de la raíz
buscada y alguna otra parte de la función “atrapa” la iteración.

24. Newton – Raspón
Ejemplo
Determine la raíz positiva mínima de f(x)= 7sen(x)e –x -1
Solución
Graficando la función se puede ver que existen dos raíces positivas, la raíz mínima esta
muy cerca al origen, por lo que se tomará como valor inicial.

25. Newton – Raspón
Ejemplo
valor inicial x0=0, y tomando en cuenta un error admisible de 10-5,
Por lo que se utilizaran 6 decimales.
Donde:

26. Newton – Raspón
Ejemplo
1ra Iteración 2da Iteración
4ta Iteración
3ra Iteración

27. Newton – Raspón
Resultado
Luego de realizar 4 iteraciones se tiene el siguiente resultado
X=0.170180
Error=10-6

28. Punto fijo
Definición
Es un método iterativo que permite
resolver sistemas de ecuaciones que no
necesariamente son lineales. Se puede
utilizar para determinar raíces de una
función de la forma f(x), siempre que se
cumplan los criterios de convergencia.

29. Punto fijo
Definición
El método de iteración de punto fijo, también denominado método de
aproximación sucesiva, requiere volver a escribir la ecuación f(x)=0 en
la forma x= g(x).
Se iguala a cero para que la x quede a la izquierda.
x=g(x) donde g(x) es el despeje de x en f(x)
Existen dos maneras de hacerlo
1. Despejando la variable x
2. Sumando x a ambos lados de la ecuación

30. Punto fijo
Despejando la variable X
Ejemplo: f(x)=3x²- 4x +5
Primero se iguala a cero la función
3x²- 4x +5=0
Luego se despeja la variable x
x=3x²+5 g(x)
4

31. Punto fijo
Sumando x en ambos lados de la ecuación
Ejemplo: f(x)= cos(x)
primero se iguala a cero la función
cos(x)=0
Luego se suma la variable x en ambos lados
x= cos(x)+x g(x)

32. Punto fijo
Función convergente
Es aquella función que se acerca a un punto fijo.
Condición |g´(x)| < 1
El método de punto fijo inicia con una aproximación
inicial X₀ y X¡₊₁ = g(X¡) que genera una sucesión de
aproximaciones la cual converge a la solución de la
ecuación f(x) = 0.

33. Punto fijo
Teorema del Punto Fijo
Si g es una función continua en [a,b] y g(x) Ɛ[a,b]para
todo x Ɛ[a,b], entonces g tiene por lo menos un punto
fijo en [a,b]

34. Punto fijo
Ejercicio
De la siguiente ecuación: f(x) x3 -10x-5
Despejando x, se tiene las siguientes ecuaciones de la forma x= g(x):
Calculamos la raíz por el método de punto fijo, tomando en cuenta el criterio y el
valor inicial x0 =1, en ambos casos, y determinar cual ecuación converge a una raíz f(x).

35. Punto fijo
Ejercicio
Solución
a) De la ecuación g(x)= se obtiene de la derivada
1ra. Iteración
Utilizando el valor inicial x0=1, se tiene los siguientes Valores
Como el error aun es relativamente grande se tendrá que realizar otro iteración

36. Punto fijo
Ejercicio
Solución
El resultado del criterio de convergencia esta muy cercano a 1 por lo que se puede decir que el
Método converge a un resultado pero que por el momento será lentamente.
2da. Iteración

37. Punto fijo
Ejercicio
Solución
3ra. Iteración

38. Punto fijo
Ejercicio
Solución
Los valores de las próximas iteraciones se
muestran en la siguiente tabla:
i Xi (g´(xi)) (xi-xi-1)
0 1.00000
1 2.46621 1.07682 1.46621
2 3.09552 1.00993 0.62931
3 3.30056 0.99143 0.20503
4 3.36214 0.98613 0.06158
5 3.38020 0.98460 0.01806
6 3.38546 0.98416 0.00526
7 3.38699 0.98403 0.00153
8 3.38744 0.98399 0.00044
9 3.38757 0.98398 0.00013
10 3.388760 0.98398 0.00004

39. Punto fijo
Ejercicio
Respuesta
La raíz de la ecuación es la siguiente:
X10=3.38760
Error=4.10-5

40. Conclusion
Una vez culminada la siguiente investigación se dan ciertos aspectos de interés sobre los métodos
Numérico principalmente su definición, aplicación y ejercicios que permitirán ayudar la compresión de este tema
cabe destacar el uso de tecnología que permitan llevar el conocimiento a donde se requiera.
Nos hemos empeñados en incluir cálculos de ecuaciones con lo diferentes métodos, con el fin de enriquecer la presentación.
Sin embargo, algunas veces tal material representa un escollo para el estudiante novato.
Es por ello que hemos explicado lo mas simple posible, para cumplir con el objetivo de esta presentación
Este material permitirá ayudar con el problema matemático que existe en nuestra sistema de educación.
Permitirá a los estudiantes contar con herramientas para el aprendizaje de análisis numérico en el área de ingeniería
de la población Venezolana y mas allá de estas frontera ya que este materia educativo será publicado en Internet.

41. Bibliografía
Electrónicos
Método de la bisección
https://tecdigital.tec.ac.cr/revistamatematica/HERRAmInternet/ecuaex
ecl/node4.html
Disponible en
Interpolación Lineal: Método, Ejercicios
https://www.lifeder.com/interpolacion-linealDisponible en
http://test.cua.uam.mx/MN/Methods/Raices/NewtonRaphson/NewtonRa
phson.php
Disponible en
Método Newton Raphson
https://matematica.laguia2000.com/general/interpolacion-lineal
https://www.academia.edu/12097541/Metodo_del_punto_fijo_Metodos_
Numericos_2
Disponible en
Método del punto fijo