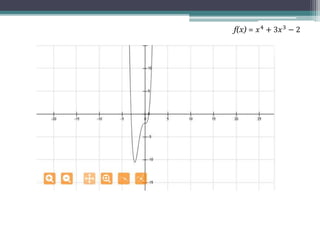
El documento describe el método de bisección para encontrar raíces de una función. Este método involucra repetidamente dividir el intervalo que contiene la raíz a la mitad basado en si la función es positiva o negativa a mitad del intervalo, hasta que la aproximación a la raíz cambia menos de un porcentaje especificado. Se provee un ejemplo completo de aplicar este método para encontrar la raíz de la función x4 + 3x3 - 2 hasta un error porcentual del 1%.

2. El método de bisección se basa en el
Teorema del Valor Intermedio:
Sea f(x) continua en un intervalo [a,b] y
supongamos que f(a) < f(b). Entonces para cada
z tal que f(a)< z <f(b) , existe un 𝒙 𝟎 ∈ (𝒂, 𝒃) tal
que f(𝒙 𝟎)= z.
La misma conclusión se obtiene para el caso que
f(a) > f(b)

3. En particular, si f(a) y f(b) tienen signos
opuestos, entonces un valor intermedio es
precisamente z=0, y por lo tanto, el Teorema del
Valor Intermedio nos asegura que debe existir 𝒙 𝟎 ∈
𝒂, 𝒃 tal que f(𝒙 𝟎)=0, es decir, debe haber por lo
menos una raíz de f(x) en el intervalo (a,b).

4. El método de bisección sigue los siguientes pasos:
Sea f(x) continua
i) Encontrar valores iniciales 𝒙 𝒂 , 𝒙 𝒃 tales que f(𝒙 𝒂)
y f(𝒙 𝒃) tienen signos opuestos, es decir:
f(𝒙 𝒂) ∙ f(𝒙 𝒃) < 0

5. ii) La primera aproximación a la raíz se toma igual
al punto medio entre 𝒙 𝒂 y 𝒙 𝒃 :
𝒙 𝒓 =
𝒙 𝒂 + 𝒙 𝒃
𝟐
iii) Evaluar f(𝒙 𝒓). Forzosamente debemos caer en
uno de los siguientes casos:
a) f(𝒙 𝒂) ∙ f(𝒙 𝒓) < 0
En este caso, tenemos que f(𝒙 𝒂) y f(𝒙 𝒓) tienen
signos opuestos, y por lo tanto la raíz se encuentra
en el intervalo [𝒙 𝒂 , 𝒙 𝒓].

6. b) f(𝒙 𝒂) ∙ f(𝒙 𝒓) > 0
En este caso, tenemos que f(𝒙 𝒂) y f(𝒙 𝒓) tienen el
mismo signo, y de aquí que f(𝒙 𝒓) y f(𝒙 𝒃) tienen
signos opuestos. Por lo tanto, la raíz se encuentra
en el intervalo [𝒙 𝒓 , 𝒙 𝒃].
c) f(𝒙 𝒂) ∙ f(𝒙 𝒓) = 0
En este caso se tiene que f(𝒙 𝒓) = 0 y por lo tanto ya
localizamos la raíz. El proceso se vuelve a repetir
con el nuevo intervalo, hasta que:

7. 𝑥 𝑟 𝑎𝑐𝑡𝑢𝑎𝑙−𝑥 𝑟 𝑝𝑟𝑒𝑣𝑖𝑎
𝑥 𝑟 𝑎𝑐𝑡𝑢𝑎𝑙
× 100% < 𝜀
Ejemplo:
Aplique el metodo de biseccion para encontrar la
raíz de la función 𝑥4 + 3𝑥3 − 2, hasta encontrar la
raíz o que el Ep=1%.
Lo primero que se hace es tabular, y en cuanto se
obtenga el primer cambio de signo utilizamos los
intervalos para utilizar la primer formula

8. f(x) = 𝑥4 + 3𝑥3 − 2

9. x f(x)
-1.5 -7.06
-1 -4
0 -2
1 2
1.5 13.18
𝒙 𝒂 = valor menor del intervalo
𝒙 𝒃 = valor mayor del intervalo
𝒙 𝒂 = 0 𝒙 𝒃 = 1
𝒙 𝒓 =
𝒙 𝒂 + 𝒙 𝒃
𝟐
=
0 + 𝟏
𝟐
= 0.5
Sustituimos en la función
𝑥4 + 3𝑥3 − 2:
(0.5)4+ 3(0.5)3−2 = −1.56
f(𝑥 𝑎) ∙ f(𝑥 𝑟)
f(0) ∙ f(0.5)
(-2)(-1.56)= 3.12 > 0; 𝑥 𝑟 sustituye a 𝑥 𝑎

10. Iteración 2
𝒙 𝒂 = 0.5 𝒙 𝒃 = 1
𝒙 𝒓 =
0.5 + 𝟏
𝟐
= 0.75
𝐸 𝑝 =
𝑥 𝑟 𝑎𝑐𝑡𝑢𝑎𝑙−𝑥 𝑟 𝑝𝑟𝑒𝑣𝑖𝑎
𝑥 𝑟 𝑎𝑐𝑡𝑢𝑎𝑙
× 100% =
0.75−0.5
0.75
× 100 = 33%
El porcentaje es muy lejano al 1% entonces continuamos haciendo
interacciones
Sustituimos (0.75)4+ 3(0.75)3−2 = −0.41
f(𝑥 𝑎) ∙ f(𝑥 𝑟)
(-1.56)(-0.41)= 0.63 > 0; 𝑥 𝑟 sustituye a 𝑥 𝑎

11. Iteración 3
𝒙 𝒂 = 0.75 𝒙 𝒃 = 1
𝒙 𝒓 =
0.75 + 𝟏
𝟐
= 0.87
𝐸 𝑝=
0.87−0.5
0.87
× 100 = 13%
El porcentaje es muy lejano al 1% entonces continuamos haciendo
interacciones
Sustituimos (0.87)4+ 3(0.87)3−2 = 0.54
f(𝑥 𝑎) ∙ f(𝑥 𝑟)
(-0.41)(0.54)= -0.22 < 0; 𝑥 𝑟 sustituye a 𝑥 𝑏

12. Iteración 4
𝒙 𝒂 = 0.75 𝒙 𝒃 = 0.87
𝒙 𝒓 =
0.75 + 0 .87
𝟐
= 0.81
𝐸 𝑝=
0.81−0.87
0.81
× 100 = 7%
Sustituimos (0.81)4
+ 3(0.81)3
−2 = 0.02
f(𝑥 𝑎) ∙ f(𝑥 𝑟)
(-0.41)(0.02)= -8.2x10−3 < 0; 𝑥 𝑟 sustituye a 𝑥 𝑏

13. Iteración 5
𝒙 𝒂 = 0.75 𝒙 𝒃 = 0.81
𝒙 𝒓 =
0.75 + 0 .8𝟏
𝟐
= 0.78
𝐸 𝑝=
0.78−0.81
0.78
× 100 = 3%
Sustituimos (0.78)4
+ 3(0.78)3
−2 = −0.20
f(𝑥 𝑎) ∙ f(𝑥 𝑟)
(-0.41)(-0.20)= 0.08 > 0; 𝑥 𝑟 sustituye a 𝑥 𝑎

14. Iteración 6
𝒙 𝒂 = 0.78 𝒙 𝒃 = 0.81
𝒙 𝒓 =
0.78 + 0 .81
𝟐
= 0.79
𝐸 𝑝=
0.79−0.78
0.79
× 100 = 1%
𝒙 𝒓 = 𝟎. 𝟕𝟗 es la raíz de la función 𝑥4
+ 3𝑥3
− 2